|
☆☆☆ 点击下载试题 ☆☆☆  2018曲靖市中考数学模拟真题【精编Word版含答案解析】由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ 一、选择题．（共8小题，每小题3分，共24分．） 1．（3分）一元二次方x2﹣3x+3=0的根的情况是（ ） A．有两个相等的实数根 B．有两个不相等的实数根 C．只有一个相等的实数根 D．没有实数根 2．（3分）二次函数y=（m﹣2）x2+5x﹣3m的图象开口向下，则m的取值范围（ ） A．m≤2 B．m＜2 C．m≥2 D．m＞2 3．（3分）二次函数y=ax2+bx+c图象上部分点的坐标满足下表：
则该函数图象的顶点坐标为（ ） A．（﹣3，﹣3） B．（﹣2，﹣2） C．（﹣1，﹣3） D．（0，﹣6） 4．（3分）若关于x的一元二次方程kx2﹣2（k﹣1）x+k+1=0有实数根，则k的取值范围是（ ） A．k＜  且k≠0 B．k≤ C．k≤且k≠0 D．k为任意数5．（3分）若α，β是一元二次方程x2﹣3x+1=0的两根，则α2+β2的值是（ ） A．6 B．7 C．8 D．9 6．（3分）抛物线y=（x+2）2﹣3可以由抛物线y=x2平移得到，则下列平移过程正确的是（ ） A．先向左平移2个单位，再向上平移3个单位 B．先向左平移2个单位，再向下平移3个单位 C．先向右平移2个单位，再向下平移3个单位 D．先向右平移2个单位，再向上平移3个单位 7．（3分）已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（﹣1，0），（3，0）．对于下列命题：①2a+b=0；②abc＜0；③b2﹣4ac＞0；④8a+c＞0．其中正确的有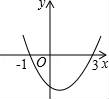（ ）  A．3个 B．2个 C．1个 D．0个 8．（3分）已知二次函数y=﹣x2﹣7x+  ，若自变量x分别取x1，x2，x3，且0＜x1＜x2＜x3，则对应的函数值y1，y2，y3的大小关系正确的是（ ）A．y1＞y2＞y3 B．y1＜y2＜y3 C．y2＞y3＞y1 D．y2＜y3＜y1 二、填空题．（共8题，每题3分．） 9．（3分）若x=﹣2是关于x的一元二次方程x2﹣  ax+a2=0的一个根，则a的值为 ．10．（3分）若二次函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是 ． 11．（3分）某一型号飞机着陆后滑行的距离y（单位：m）与滑行时间x（单位：s）之间的函数关系式是y=  60x﹣1.5x2，该型号飞机着陆后滑行 m才能停下来．12．（3分）若抛物线的顶点坐标为（0，3），开口向下，请写出一个符合条件的抛物线的解析式： ． 13．（3分）若m是方程x2﹣x+1=0的一根；则m2﹣m+2016的值是 ． 14．（3分）方程x2﹣9x+18=0的两个根是等腰三角形的底和腰的长，则这个等腰三角形的周长为 ． 15．（3分）已知a、b实数且满足（a2+b2）2﹣（a2+b2）﹣6=0，则a2+b2的值为 ． 16．（3分）抛物线y=﹣x2+2x+3与x轴交于A，B两点，与y轴交于C，抛物线的顶点为M （1）△ABC的面积= ，△ABM的面积= ． （2）利用图象可得，当x满足 时，0≤y≤3． 三、解答题． 17．（8分）解方程． （1）3x（x﹣2）= 4﹣2x； （2）2x2﹣5x+1=0． 18．（7分）阅读材料：如果方程x2+px+q=0的两个根是x1，x2，那么x1+x2=﹣p； x1x2=q，请根据以上结论，解决下列问题： （1）已知x1，x2是方程x2﹣4x+2=0的两根，求： ①  的值； ②  的值．19．（7分）如图，有一个长为24米的篱笆，一面有围墙（墙的最大长度为10米）围成中间隔有一道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S米2． （1）求S与x的函数关系式及x的取值范围． （2）如果要围成的花圃ABCD的面积是45平方米，则AB的长为多少米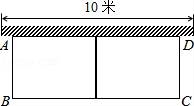？  20．（10分）我国中东部地区雾霾天气趋于严重，环境治理已刻不容缓．我市某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务． （1）试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围； （2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？ 21．（10分）两年前，某种化肥的生产成本是2500元/吨，随着生产技术的改进，今年，该化肥的生产成本下降1600元/吨． （1）求前两年该化肥成本的年平均下降率； （2）如果按此下降率继续下降，再过两年，该化肥的生产成本是否会降到1000元/吨，请说明理由． 22．（9分）已知二次函数y=ax2+b的图象与直线y=x+2相交于点A（1，．m）和点B（n，0）． （1）试确定点A、点B的坐标； （2）确定二次函数的解析式； （3）在给出的平面直角坐标系中画出这样两个函数图象的草图，并结合图象直接写出ax2+b＞x+2时，x的取值范围． 23．（9分）如图，在矩形ABCD中，AB=6厘米，BC=12厘米，点P从点A出发，沿AB边向点B以1厘米/秒的速度移动，同时点Q从点B出发沿BC边向点C以2厘米/秒的速度移动，如果P、Q两点在分别到达B、C两点后停止移动，回答下列问题： （1）P、Q两点开始运动后第几秒时，三角形PBQ的面积等于8平方厘米？ （2）设P、Q两点开始运动后第t秒时，五边形APQCD的面积为S（平方厘米），写出S与t的函数关系式，并指出自变量t的取值范围； （3）当t为何值时，S最小？求出S的最 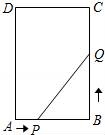小值？ 24．（12分）如图，已知抛物线y=  （x﹣2）（x+a）（a＞0）与x轴将交于B，C，与y轴交于点E，且点B在C的左侧．（1）若抛物线过点M（﹣2，﹣2），求实数a的值； （2）在（1）的条件下，解答下列问题： ①求出△BCE的面积； ②在抛物线的对称轴上找一点H，使CH+EH的值最小，求出H点的坐标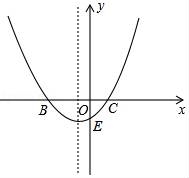．  2018曲靖市中考数学模拟真题参考答案与试题解析 一、选择题．（共8小题，每小题3分，共24分．） 1．（3分）一元二次方x2﹣3x+3=0的根的情况是（ ） A．有两个相等的实数根 B．有两个不相等的实数根 C．只有一个相等的实数根 D．没有实数根 【解答】解：∵△=b2﹣4ac=（﹣3）2﹣4×1×3=﹣3＜0， ∴方程没有实数根， 故选：D． 2．（3分）二次函数y=（m﹣2）x2+5x﹣3m的图 象开口向下，则m的取值范围（ ）A．m≤2 B．m＜2 C．m≥2 D．m＞2 【解答】解：根据题意得：m﹣2＜0， 解得：m＜2． 故选：B． 3．（3分）二次函数y=ax2+bx+c图象上部分点的坐标满足下表：
则该函数图象的顶点坐标为（ ） A．（﹣3，﹣3） B．（﹣2，﹣2） C．（﹣1，﹣3 ） D．（0，﹣6）【解答】解：∵x=﹣3和﹣1时的函数值都是﹣3相等， ∴二次函数的对称轴为直线x=﹣2， ∴顶点坐标为（﹣2，﹣2）． 故选：B． 4．（3分）若关于x的一元二次方程kx2﹣2（k﹣1）x+k+1=0有实数根，则k的取值范围是（ ） A．k＜  且k≠0 B．k≤ C．k≤且k≠0 D．k为任意数【解答】解：∵关于x的一元二次方程kx2﹣2（k﹣1）x+k+1=0有实数根， ∴  ，即[﹣2（k﹣1）]2﹣4k（k+1）≥0，解得k≤ 且k≠0．故选：C． 5．（3分）若α，β是一元二次方程x2﹣3x  +1=0的两根，则α2+β2的值是（ ）A．6 B．7 C．8 D．9 【解答】解：根据题意得α+β=3，αβ=1， 所以α2+β2=（α+ β）2﹣2αβ=32﹣2×1=7．故选：B． 6．（3分）抛物线y=（x+2）2﹣3可以由抛物线y=x2平移得到，则下列平移过程正确的是（ ）  A．先向左平移2个单位，再向上平移3个单位B．先向左平移2个单位，再向下平移3个单位 C．先向右平移2个单位，再向下平移3个单位 D．先向右平移2个单位，再向上平移3个单位 【解答】解：抛物线y=x2向左平移2个单位可得到抛物线y=（x+2）2， 抛物线y=（x+2）2，再向下平移3个单位即可得到抛物线y=（x+2）2﹣3． 故平移过程为：先向左平移2个单位，再向下平移3个单位． 故选：B． 7．（3分）已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（﹣1，0），（3，0）．对于下列命题：①2a+b=0；②abc＜0；③b2﹣4ac＞0；④8a+c＞0．其中正确的有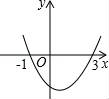（ ）  A．3个 B．2个 C．1个 D．0个 【解答】解：A．①因为点（﹣1，0），（3，0）在二次函数上，所以a﹣b+c=0，9a+3b+c=0，两式作差可得8a+4b=0，故2a+b=0，则①正确；②由图形可知，该二次函数的a＞0，c＜0，顶点的横坐标﹣  =1＞0，则b＜0，知abc＞0，故②错误；③函数图象与x轴两个交点，可知b2﹣4ac＞0，故③正确； ④由图象可知  ，则b=﹣2a，因（3，0）在函数图象上，故9a+3b+c=0，将b=﹣2a代入得3a+c=0，由函数图象知a＞0，故3a+c+5a＞0，即8a+c＞0．故④正确．故选项A正确； B．①因为点（﹣1，0），（3，0）在二次函数上，所以a﹣b+c=0，9a+3b+c=0，两式作差可得8a+4b=0，故2a+b=0，则①正确； ②由图形可知，该二次函数的a＞0，c＜0，顶点的横坐标﹣ =1＞0，则b＜0，知abc＞0，故②错误；③函数图象与x轴两个交点，可知b2﹣4ac＞0，故③正确； ④由图象可知 ，则b=﹣2a，因（3，0）在函数图象上，故9a+3b+c=0，将b=﹣2a代入得3a+c=0，由函数图象知a＞0，故3a+c+5a＞0，即8a+c＞0．故④正确．故选项B错误； C．①因为点（﹣1，0），（3，0）在二次函数上，所以a﹣b+c=0，9a+3b+c=0，两式作差可得8a+4b=0，故2a+b=0，则①正确； ②由图形可知，该二次函数的a＞0，c＜0，顶点的横坐标﹣ =1＞0，则b＜0，知abc＞0，故②错误；③函数图象与x轴两个交点，可知b2﹣4ac＞0，故③正确； ④由图象可知 ，则b=﹣2a，因（3，0）在函数图象上，故9a+3b+c=0，将b=﹣2a代入得3a+c=0，由函数图象知a＞0，故3a+c+5a＞0，即8a+c＞0．故④正确．故 选项C错误；D．①因为点（﹣1，0），（3，0）在二次函数上，所以a﹣b+c=0，9a+3b+c=0，两式作差可得8a+4b=0，故2a+b=0，则①正确； ②由图形可知，该二次函数的a＞0，c＜0，顶点的横坐标﹣  =1＞0，则b＜0，知abc＞0，故②错误；③函数图象与x轴两个交点，可知b2﹣4ac＞0，故③正确； ④由图象可知  ，则b=﹣2a，因（3，0）在函数图象上，故9a+3b+c=0，将b=﹣2a代入得3a+c=0，由函数图象知a＞0，故3a+c+5a＞0，即8a+c＞0．故④正确．故选项D错误． 故选：A． 8．（3分）已知二次函数y=﹣x2﹣7x+  ，若自变量x分别取x1，x2，x3，且0＜x1＜x2＜x3，则对应的函数值y1，y2，y3的大小关系正确的是（ ）A．y1＞y2＞y3 B．y1＜y2＜y3 C．y2＞y3＞y1 D．y2＜y3＜y1 【解答】解：抛物线的对称轴为直线x=﹣  =﹣ ，而抛物线开口向下， 所以当x＞﹣ 时，y随x的增大而减小， 所以当0＜x1＜x2＜x3时，y1＞y2＞y3． 故选：A． 二、填空题．（共8题，每题3分．） 9．（3分）若x=﹣2是关于x的一元二次方程x2﹣ ax+a2=0的一个根，则a的值为 ﹣1或﹣4 ．【解答】解：∵x=﹣2是关于x的一元二次方程x2﹣ ax+a2=0的一个根，∴（﹣2）2﹣ a×（﹣2）+a2=0，即a2+5a+4=0，整理，得（a+1）（a+4）=0， 解得 a1=﹣1，a2=﹣4． 即a的值是﹣1或﹣4． 故 答案是：﹣1或﹣4．10．（3分）若二次函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是 1 ． 【解答】解：∵二次函数y=mx2+2x+1的图象与x轴只有一个公共点， ∴△=4﹣4m=0，且m≠0， 解得 m=1． 故答案是：1． 11．（3分）某一型号飞机着陆后滑行的距离y（单位：m）与滑行时间x（单位：s）之间的函数关系式是y=60x﹣1.5x2，该型号飞机着陆后滑行 600 m才能停下来． 【解答】解：∵a=﹣1.5＜0， ∴函数有最大值． ∴y最大值=  = =600，即飞机着陆后滑行600米才能停止． 故答案为：600． 12．（3分）若抛物线的顶点坐标为（0，3），开口向下，请写出一个符合条件的抛物线的解析式： y=﹣x2+3 ． 【解答】解：∵抛物线的顶点坐标为（0，3） ∴可设抛物线的解析式为y=ax2+3， 又∵抛物线的开口向下， ∴a＜0，故可取a=﹣1， ∴抛物线的解析式为y=﹣x2+3， 故答案为：y=﹣x2+3． 13．（3分）若m是方程x2﹣x+1=0的一根；则m2﹣m+2016的值是 2015 ． 【解答】解：把x=m代入方程得：m2﹣m+1=0 即m2﹣m=﹣1， ∴m2﹣m+2016=2015， 故答案是：2015． 14．（3分）方程x2﹣9x+18=0的两个根是等腰三角形的底和腰的长，则这个等腰三角形的周长为 15 ． 【解答】解：x2﹣9x+18=0， （x﹣3）（x﹣6）=0， 所以x1=3，x2=6， 所以等腰三角形的底为3，腰为6，这个等腰三角形的周长为3+6+6=15． 故答案为15． 15．（3分）已知a、b实数且满足（a2+b2）2﹣（a2+b2）﹣6=0，则a2+b2的值为 3 ． 【解答】解：设a2+b2=x， 则原式左边变为x2﹣x﹣6， ∴x2﹣x﹣6=0． 解得：x=3或﹣2． ∵a2+b2≥0， ∴a2+b2=3． 16．（3分）抛物线y=﹣x2+2x+3与x轴交于A，B两点，与y轴交于C ，抛物线的顶点为M（1）△ABC的面积= 6 ，△ABM的面积= 8 ． （2）利用图象可得，当x满足 ﹣1≤x≤0或2≤x≤3 时，0≤y≤3． 【解答】解：（1）∵在y=﹣x2+2x+3中，当x=0时，y=3， ∴C（0，3）， 又y=﹣x2+2x+3=﹣（x﹣3）（x+1），或y=﹣x2+2x+3=﹣（x﹣1）2+4， ∴A（﹣1，0），B（3，0），M（1，4）， ∴AB=4，OC=3，MD=4， 则S△ABC=  AB•OC= ×4×3=6；S△ABM=AB•MD=×4×4=8．故答案是：6；8； （2）根据图示知，当﹣1≤x≤0或2≤x≤3时，0≤y≤3． 故答案是：﹣1≤x≤0或2≤x≤3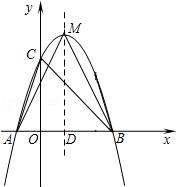．  三、解答题． 17．（8分）解方程． （1）3x（x﹣2）=4﹣2x； （2）2x2﹣5x+1=0． 【解答】解：（1）方程整理得：3x（x﹣2）+2（x﹣2）=0， 分解因式得：（x﹣2）（3x+2）=0， 可得x﹣2=0或3x+2=0， 解得：x1=2，x2=﹣  ；（2）∵a=2、b=﹣5、c=1， ∴△=25﹣4×2×1=17＞0， 则x=  ．18．（7分）阅读材料：如果方程x2+px+q=0的两个根是x1，x2，那么x1+x2=﹣p； x1x2=q，请根据以上结论，解决下列问题： （1）已知x1，x2是方程x2﹣4x+2=0的两根，求： ①  的值； ②  的值．【解答】解：（1）∵x1，x2是方程x﹣4x+2=0的两根， ∴x1+x2=4； x1x2=2， ∴①x12+x22=（x1+x2）2﹣2x1x2=42﹣2×2=12； ② = =2．19．（7分）如图，有一个长为24米的篱笆，一面有围墙（墙的最大长度为10米）围成中间隔有一道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S米2． （1）求S与x的函数关系式及x的取值范围． （2）如果要围成的花圃ABCD的面积是45平方米，则AB的长为多少米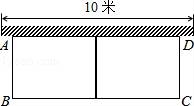？  【解答】解：（1）S=（24﹣3x）x=24x﹣3x2； 又∵x＞0，且10≥24﹣3x＞x， ∴  ≤x＜6；（2）依题意有45=24x﹣3x2， x=5或x=3； 若x=3，则AB=3m，则BC=15m＞10m，舍去． 答：AB的长为5米． 20．（10分）我国中东部地区雾霾天气趋于严重，环境治理已刻不容缓．我市某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务． （1）试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围； （2）当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？ 【解答】解：（1）根据题中条件销售价每降低10元，月销售量就可多售出50台， 则月销售量y（台）与售价x（元/台）之间的函数关系式：y=200+50×  ，化简得：y=﹣5x+2200；供货商规定这种空气净化器售价不能低于300 元/台，代理销售商每月要完成不低于450台，则  ，解得：300≤x≤350． ∴y与x之间的函数关系式为：y=﹣5x+2200（300≤x≤350）； （2）W=（x﹣200）（﹣5x+2200）， 整理得：W=﹣5（x﹣320）2+72000． ∵x=320在300≤x≤350内， ∴当x=320时，最大值为72000， 即售价定为320元/台时，商场每月销售这种空气净化器所获得的利润w最大，最大利润是72000元． 21．（10分）两年前，某种化肥的生产成本是2500元/吨，随着生产技术的改进，今年，该化肥的生产成本下降1600元/吨． （1）求前两年该化肥成本的年平均下降率； （2）如果按此下降率继续下降，再过两年，该化肥的生产成本是否会降到1000元/吨，请说明理由． 【解答】解：设前两年该化肥成本的年平均下降率为x； 依题意得：2500（1﹣x）2=1600， 化简得：（1﹣x）2=0.64， 解得：x2=0.2，x2=1.8（不合题意，舍去）． 答：前两年该化肥成本的年平均下降率为是20%； （2）1600（1﹣0.2）2=1024． ∵1024＞1000， ∴按此下降率继续下降，再过两年，该化肥的生产成本不会降到1000元/吨． 答：按此下降率继续下降，再过两年，该化肥的生产成本不会降到1000元/吨． 22．（9分）已知二次函数y=ax2+b的图象与直线y=x+2相交于点A（1，．m）和点B（n，0）． （1）试确定点A、点B的坐标； （2）确定二次函数的解析式； （3）在给出的平面直角坐标系中画出这样两个函数图象的草图，并结合图象直接写出ax2+b＞x+2时，x的取值范围． 【解答】解：（1）∵直线y=x+2经过点A（1，m）和点B（n，0）， ∴m=1+2=3，n+2=0，即n=﹣2， ∴A（1，3），B（﹣2，0）， （2）∵二次函数y=ax2+b的图象经过A（1，3），B（﹣2，0）， ∴  ，解得 ，∴二次函数的解析式为y=﹣x2+4； （3）如图，由函数图象可知，当﹣2＜x＜1时，ax2+b＞x+2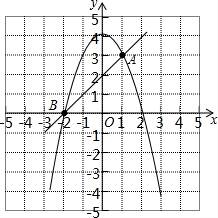．  23．（9分）如图，在矩形ABCD中，AB=6厘米，BC=12厘米，点P从点A出发，沿AB边向点B以1厘米/秒的速度移动，同时点Q从点B出发沿BC边向点C以2厘米/秒的速度移动，如果P、Q两点在分别到达B、C两点后停止移动，回答下列问题： （1）P、Q两点开始运动后第几秒时，三角形PBQ的面积等于8平方厘米？ （2）设P、Q两点开始运动后第t秒时，五边形APQCD的面积为S（平方厘米），写出S与t的函数关系式，并指出自变量t的取值范围； （3）当t为何值时，S最小？求出S的最小值？  【解答】解：（1）设P、Q两点开始运动后第n秒时，三角形PBQ的面积等于8平方厘米，则AP=n，BQ=2n， ∵AB=6， ∴BP=6﹣n， ∵  BP×BQ=8，∴ ×（6﹣n）×2n=8，解得n=2或4， ∴P、Q两点开始运动后第2或4秒时，三角形PBQ的面积等于8平方厘米； （2）∵五边形APQCD的面积=正方形ABCD的面积﹣△BPQ的面积， ∴S=6×12﹣ （6﹣t）×2t=t2﹣6t+72（0≤t≤6）；（3）∵S=t2﹣6t+72， ∴当t=﹣  =3时，S最小，S的最小值为 =63．24．（12分）如图，已知抛物线y= （x﹣2）（x+a）（a＞0）与x轴将交于B，C，与y轴交于点E，且点B在C的左侧．（1）若抛物线过点M（﹣2，﹣2），求实数a的值； （2）在（1）的条件下，解答下列问题： ①求出△BCE的面积； ②在抛物线的对称轴上找一点H，使CH+EH的值最小，求出H点的坐标． 【解答 】解：（1）将M（﹣2，﹣2）代入抛物线解析式得：﹣2= （﹣2﹣2）（﹣2+a），解得：a=4； （2）①由（1）抛物线解析式y=  （x﹣2）（x+4），当y=0时，得：0= （x﹣2）（x+4），解得：x1=2，x2=﹣4， ∵点B在点C的左侧， ∴B（﹣4，0），C（2，0）， 当x=0时，得：y=﹣2，即E（0，﹣2）， ∴S△BCE=  ×6×2=6；②由抛物线解析式y= （x﹣2）（x+4），得对称轴为直线x=﹣1，根据C与B关于抛物线对称轴直线x=﹣1对称，连接BE，与对称轴交于点H，即为所求， 设直线BE解析式为y=kx+b， 将B（﹣4，0）与E（0，﹣2）代入得：  ，解得：  ，∴直线BE解析式为y=﹣ x﹣2，将x=﹣1代入得：y= ﹣2=﹣ ，则H（﹣1，﹣ ）． (责任编辑：admin) |