|
三、解答题 32.已知:如图,在△ABC中,AB=13,AC=8,cos∠BAC=5/13,BD⊥AC,垂足为点D,E是BD的中点,联结AE并延长,交边BC于点F. 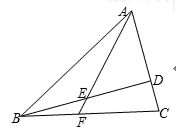 (1)求∠EAD的余切值; (2)求BF/CF的值. 答案解析: 32.(1)∠EAD的余切值为5/6;(2)BF/CF=5/8. 【解析】 【分析】 (1)在Rt△ADB中,根据AB=13,cos∠BAC=5/13,求出AD的长,由勾股定理求出BD的长,进而可求出DE的长,然后根据余切的定义求∠EAD的余切即可; (2)过D作DG∥AF交BC于G,由平行线分线段成比例定理可得CD:AD=CG:FG=3:5,从而可设CD=3x,AD=5x,再由EF∥DG,BE=ED, 可知BF=FG=5x,然后可求BF:CF的值. 【详解】 (1)∵BD⊥AC, ∴∠ADE=90°, Rt△ADB中,AB=13,cos∠BAC=5/13, ∴AD=5, 由勾股定理得:BD=12, ∵E是BD的中点, ∴ED=6, ∴∠EAD的余切=AD/ED=5/6; (2)过D作DG∥AF交BC于G, ∵AC=8,AD=5, ∴CD=3, ∵DG∥AF, ∴CD/AD=CG/FG=3/5, 设CD=3x,AD=5x, ∵EF∥DG,BE=ED, ∴BF=FG=5x, ∴BF/CF=5x/8x=5/8. 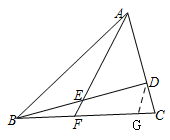 【点睛】 本题考查了勾股定理,锐角三角函数的定义,平行线分线段成比例定理.解(1)的关键是熟练掌握锐角三角函数的概念,解(2)的关键是熟练掌握平行线分线段成比例定理. (责任编辑:admin) |
