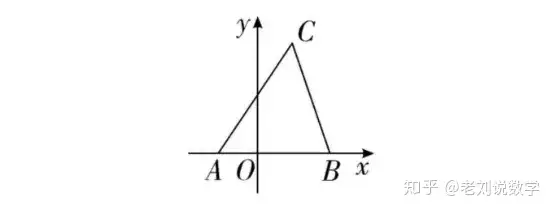');
(window.slotbydup=window.slotbydup || []).push({
id: '8096091',
container: s,
size: '580,90',
display: 'inlay-fix'
});
})();
函数图像绘制步骤:列表---描点---连线
(1)列表取值时,x≠0,因为x=0函数无意义,为了使描出的点具有代表性,可以以“0”为中心,向两边对称式取值,即正、负数各一半,且互为相反数,这样也便于求y值。
(2)由于函数图象的特征还不清楚,尽量多取一些数值,多描一些点,从而便于连线,使画出的图象更精确。
(3)连线时要用平滑的曲线按照自变量从小到大的顺序连接,切忌画成折线。
因为解析式中,x不能为0,所以y也不能为0,反比例函数的图象不可能与x轴相交,也不可能与y轴相交,但随着x无限增大或是无限减少,函数值无限趋近于0,故图像无限接近于x轴。

涉及交点情况
■ 找交点及交点个数:已知交点的某一横坐标,代入即可求出其纵坐标,反之亦然;当要求交点坐标时,将反比例函数与一次函数联立方程组,进行求解;
■ 求解交点个数:将一次函数和反比例函数联立方程组的解的个数就是交点个数。
■ 求解析式:求解析式一般需要函数图像上的点的坐标,函数图像上有几个未知数,一般需要找几个点。反比例函数的综合应用中,通常寻找交点的坐标,从而得出解析式并分别求得解析式中的常数值。

涉及面积的运用
坐标系中的图形面积问题最基本的图形为三角形,解答核心是要把点坐标转化为线段长度。
▼ 若三角形有一边在坐标轴上,通常以这条边作为三角形的底边。
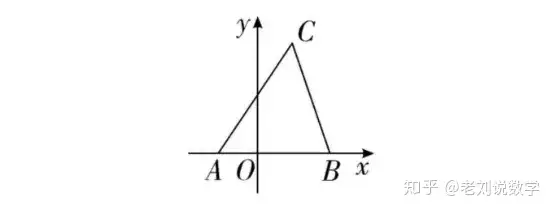
▼ 三边都不在坐标轴上,需要对图形进行割补。
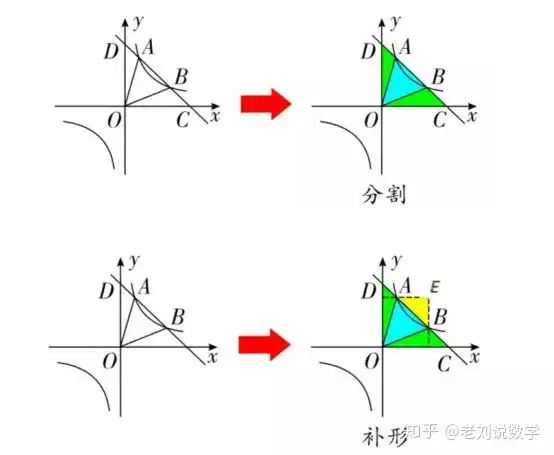
▼ 在前文性质1和2中,我们提到有关反比例函数面积的性质,此外,我们需要了解的是有关反比例函数y=k/x(k为常数且k≠0)中|k|的几何意义:过双曲线上任意一点引x轴、y轴的垂线,所得的矩形面积为|k|。
▼ 如果题目中给出线段比例和四边形的面积求k问题,利用同底等高三角形面积与高之间的关系,以及面积与k之间的关系,求出k。
注意:反比例函数图象是一种特殊的图形,它的两个分支既关于原点对称,又关于直线Y=X、Y=-X对称,因此我们做题时要充分利用反比例函数的对称性来解题。

反比例函数的存在感极强,数学考试中基本年年会遇到它,熟记其性质并灵活运用是解题的关键。我们要对此引起重视。
(责任编辑:admin) |