2023年初中数学二次函数基本概念和图像上特殊点_中考网-中考真题答案下载-中考试题库-中考成绩查询-知识点学习方法与技巧补课解题技巧学习计划表总结-中考查分网-中考网-中考资源网-中学学科网

'); (window.slotbydup=window.slotbydup || []).push({ id: '8096091', container: s, size: '580,90', display: 'inlay-fix' }); })();

以下是其基本概念和图像上特殊点。

常见三种形式。

一般式： y</mi><mo>=</mo><mi>a</mi><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mi>b</mi><mi>x</mi><mo>+</mo><mi>c</mi></math>" role="presentation" tabindex="0"> $y = a x^{2} + b x + c$
顶点式： y</mi><mo>=</mo><mi>a</mi><mrow class="MJX-TeXAtom-ORD"><mo>（</mo></mrow><mi>x</mi><mo>−</mo><mi>h</mi><msup><mrow class="MJX-TeXAtom-ORD"><mo>）</mo></mrow><mn>2</mn></msup><mo>+</mo><mi>k</mi></math>" role="presentation" tabindex="0"> $y = a （ x - h ）^{2} + k$
两根式： y</mi><mo>=</mo><mi>a</mi><mrow class="MJX-TeXAtom-ORD"><mo>（</mo></mrow><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>2</mn></msub><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $y = a （ x - x_{1}) (x - x_{2})$

（其中两根式当二次函数和x轴没有交点的时候不存在，此时可以采用更为一般的对称点式y</mi><mo>=</mo><mi>a</mi><mrow class="MJX-TeXAtom-ORD"><mo>（</mo></mrow><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>2</mn></msub><mo stretchy="false">)</mo><mo>+</mo><mi>m</mi></math>" role="presentation" tabindex="0"> $y = a （ x - x_{1}) (x - x_{2}) + m$ ，相当于函数 y</mi><mo>=</mo><mi>a</mi><mrow class="MJX-TeXAtom-ORD"><mo>（</mo></mrow><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>2</mn></msub><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $y = a （ x - x_{1}) (x - x_{2})$ 和直线y=m的两个交点，m为足够大的数）

其中出现过的字母有

a：二次项系数，在三个表达式中都出现过。代表开口大小。

b：一般式的一次项系数。

c：常数项系数

h：顶点式中顶点x坐标

k：顶点式中顶点y坐标

（此处会注意到为什么h前面是有负号，而k前面没有，如有疑惑，请看下面链接）
yi zhang：初中数学--函数平移为什么是左加右减，上加下减97 赞同 · 16 评论文章

x_1: 两根式其中一个根

x_2：两根式其中另一个根

以下我以开口向上且和x轴有两个根的二次函数为例，介绍下三个表达式的联系以及适用范围。

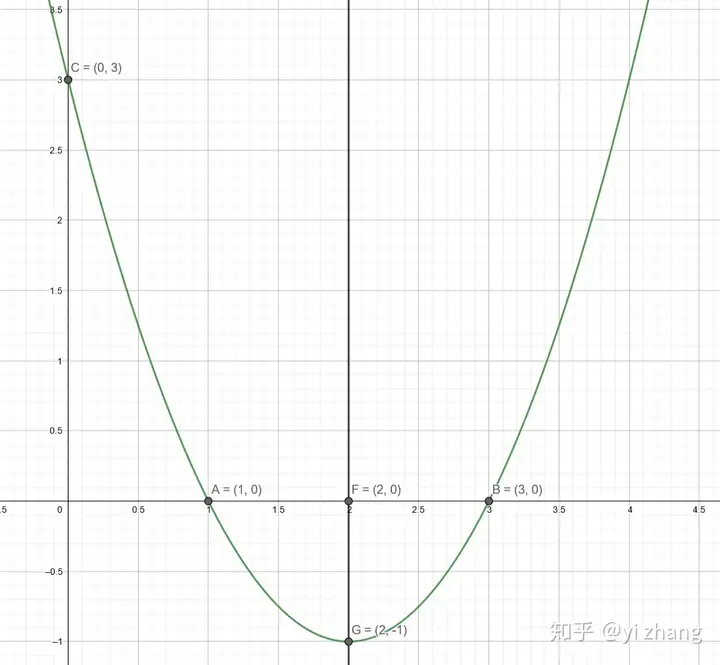
如下图为例子：

（实际函数为一般式： y</mi><mo>=</mo><msup><mi>x</mi><mn>2</mn></msup><mo>−</mo><mn>4</mn><mi>x</mi><mo>+</mo><mn>3</mn></math>" role="presentation" tabindex="0"> $y = x^{2} - 4 x + 3$ 或者写成顶点式： y</mi><mo>=</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><mn>2</mn><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo>−</mo><mn>1</mn></math>" role="presentation" tabindex="0"> $y = (x - 2)^{2} - 1$ 两根式: y</mi><mo>=</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><mn>1</mn><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><mn>3</mn><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $y = (x - 1) (x - 3)$ )

我们先认为 <mi>x</mi><mn>1</mn></msub><mo><</mo><msub><mi>x</mi><mn>2</mn></msub><mrow class="MJX-TeXAtom-ORD"><mo>，</mo></mrow></math>" role="presentation" tabindex="0"> $x_{1} < x_{2} ，$

那么可以得到几个点的坐标。

A</mi><mo>=</mo><mo stretchy="false">(</mo><msub><mi>x</mi><mn>1</mn></msub><mo>,</mo><mn>0</mn><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $A = (x_{1}, 0)$

B</mi><mo>=</mo><mo stretchy="false">(</mo><msub><mi>x</mi><mn>2</mn></msub><mo>,</mo><mn>0</mn><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $B = (x_{2}, 0)$

C</mi><mo>=</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mi>c</mi><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $C = (0, c)$

F</mi><mo>=</mo><mo stretchy="false">(</mo><mn>0</mn><mo>,</mo><mi>h</mi><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $F = (0, h)$

G</mi><mo>=</mo><mo stretchy="false">(</mo><mi>h</mi><mo>,</mo><mi>k</mi><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $G = (h, k)$

在此可以注意到，

三个式子里面都有a。

2. b未出现，c是和y轴交点坐标属于一般式的。

3. h，k是属于顶点式的。（h，k）就是顶点坐标。

4. <mi>x</mi><mn>1</mn></msub><mo>,</mo><msub><mi>x</mi><mn>2</mn></msub></math>" role="presentation" tabindex="0"> $x_{1}, x_{2}$ 是属于两根式的。分别是和x轴的两个交点。

但既然同一个二次函数可以用三种方式来表达。那么很显然，三者之间必定存在关系，以及能够相互转化。

（其实上面说法不准确，对于和x轴没有交点的无法采用两根式）

一般式和顶点式

将一般式化成顶点式（这是任何情况下都成立的）

y</mi><mo>=</mo><mi>a</mi><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mi>b</mi><mi>x</mi><mo>+</mo><mi>c</mi></math>" role="presentation" tabindex="0"> $y = a x^{2} + b x + c$

y</mi><mo>=</mo><mi>a</mi><mo stretchy="false">(</mo><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mfrac><mi>b</mi><mi>a</mi></mfrac><mi>x</mi><mo stretchy="false">)</mo><mo>+</mo><mi>c</mi></math>" role="presentation" tabindex="0"> $y = a (x^{2} + \frac{b}{a} x) + c$

y</mi><mo>=</mo><mi>a</mi><mo stretchy="false">(</mo><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mfrac><mi>b</mi><mi>a</mi></mfrac><mi>x</mi><mo>+</mo><mo stretchy="false">(</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo>−</mo><mo stretchy="false">(</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo stretchy="false">)</mo><mo>+</mo><mi>c</mi></math>" role="presentation" tabindex="0"> $y = a (x^{2} + \frac{b}{a} x + (\frac{b}{2 a})^{2} - (\frac{b}{2 a})^{2}) + c$

y</mi><mo>=</mo><mi>a</mi><mo stretchy="false">(</mo><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mfrac><mi>b</mi><mi>a</mi></mfrac><mi>x</mi><mo>+</mo><mo stretchy="false">(</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo stretchy="false">)</mo><mo>−</mo><mi>a</mi><mo stretchy="false">(</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo>+</mo><mi>c</mi></math>" role="presentation" tabindex="0"> $y = a (x^{2} + \frac{b}{a} x + (\frac{b}{2 a})^{2}) - a (\frac{b}{2 a})^{2} + c$

y</mi><mo>=</mo><mi>a</mi><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo>−</mo><mi>a</mi><mo stretchy="false">(</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo>+</mo><mi>c</mi></math>" role="presentation" tabindex="0"> $y = a (x + \frac{b}{2 a})^{2} - a (\frac{b}{2 a})^{2} + c$

y</mi><mo>=</mo><mi>a</mi><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo>+</mo><mfrac><mrow><mn>4</mn><mi>a</mi><mi>c</mi><mo>−</mo><msup><mi>b</mi><mn>2</mn></msup></mrow><mrow><mn>4</mn><mi>a</mi></mrow></mfrac></math>" role="presentation" tabindex="0"> $y = a (x + \frac{b}{2 a})^{2} + \frac{4 a c - b^{2}}{4 a}$

通过对比 y</mi><mo>=</mo><mi>a</mi><mrow class="MJX-TeXAtom-ORD"><mo>（</mo></mrow><mi>x</mi><mo>−</mo><mi>h</mi><msup><mrow class="MJX-TeXAtom-ORD"><mo>）</mo></mrow><mn>2</mn></msup><mo>+</mo><mi>k</mi></math>" role="presentation" tabindex="0"> $y = a （ x - h ）^{2} + k$ 可以发现

h</mi><mo>=</mo><mo>−</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac></math>" role="presentation" tabindex="0"> $h = - \frac{b}{2 a}$

k</mi><mo>=</mo><mfrac><mrow><mn>4</mn><mi>a</mi><mi>c</mi><mo>−</mo><msup><mi>b</mi><mn>2</mn></msup></mrow><mrow><mn>4</mn><mi>a</mi></mrow></mfrac></math>" role="presentation" tabindex="0"> $k = \frac{4 a c - b^{2}}{4 a}$

2. 一般式和两根式

由， y</mi><mo>=</mo><mi>a</mi><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo>+</mo><mfrac><mrow><mn>4</mn><mi>a</mi><mi>c</mi><mo>−</mo><msup><mi>b</mi><mn>2</mn></msup></mrow><mrow><mn>4</mn><mi>a</mi></mrow></mfrac></math>" role="presentation" tabindex="0"> $y = a (x + \frac{b}{2 a})^{2} + \frac{4 a c - b^{2}}{4 a}$

令y=0

就能得到一元二次方程的求根公式

0</mn><mo>=</mo><mi>a</mi><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo>+</mo><mfrac><mrow><mn>4</mn><mi>a</mi><mi>c</mi><mo>−</mo><msup><mi>b</mi><mn>2</mn></msup></mrow><mrow><mn>4</mn><mi>a</mi></mrow></mfrac></math>" role="presentation" tabindex="0"> $0 = a (x + \frac{b}{2 a})^{2} + \frac{4 a c - b^{2}}{4 a}$

0</mn><mo>=</mo><mo stretchy="false">(</mo><mi>x</mi><mo>+</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo>+</mo><mfrac><mrow><mn>4</mn><mi>a</mi><mi>c</mi><mo>−</mo><msup><mi>b</mi><mn>2</mn></msup></mrow><mrow><mn>4</mn><msup><mi>a</mi><mn>2</mn></msup></mrow></mfrac></math>" role="presentation" tabindex="0"> $0 = (x + \frac{b}{2 a})^{2} + \frac{4 a c - b^{2}}{4 a^{2}}$

(</mo><mi>x</mi><mo>+</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mo>=</mo><mfrac><mrow><msup><mi>b</mi><mn>2</mn></msup><mo>−</mo><mn>4</mn><mi>a</mi><mi>c</mi></mrow><mrow><mn>4</mn><msup><mi>a</mi><mn>2</mn></msup></mrow></mfrac></math>" role="presentation" tabindex="0"> $(x + \frac{b}{2 a})^{2} = \frac{b^{2} - 4 a c}{4 a^{2}}$

x</mi><mo>+</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac><mo>=</mo><mo>±</mo><mfrac><msqrt><msup><mi>b</mi><mn>2</mn></msup><mo>−</mo><mn>4</mn><mi>a</mi><mi>c</mi></msqrt><mrow><mn>2</mn><mi>a</mi></mrow></mfrac></math>" role="presentation" tabindex="0"> $x + \frac{b}{2 a} = \pm \frac{\sqrt{b^{2} - 4 a c}}{2 a}$

<mi>x</mi><mn>1</mn></msub><mo>,</mo><msub><mi>x</mi><mn>2</mn></msub><mo>=</mo><mfrac><mrow><mo>−</mo><mi>b</mi><mo>±</mo><msqrt><msup><mi>b</mi><mn>2</mn></msup><mo>−</mo><mn>4</mn><mi>a</mi><mi>c</mi></msqrt></mrow><mrow><mn>2</mn><mi>a</mi></mrow></mfrac></math>" role="presentation" tabindex="0"> $x_{1}, x_{2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

按照前面的预设 <mi>x</mi><mn>1</mn></msub><mo><</mo><msub><mi>x</mi><mn>2</mn></msub></math>" role="presentation" tabindex="0"> $x_{1} < x_{2}$

那么 <mi>x</mi><mn>1</mn></msub><mo>=</mo><mfrac><mrow><mo>−</mo><mi>b</mi><mo>−</mo><msqrt><msup><mi>b</mi><mn>2</mn></msup><mo>−</mo><mn>4</mn><mi>a</mi><mi>c</mi></msqrt></mrow><mrow><mn>2</mn><mi>a</mi></mrow></mfrac></math>" role="presentation" tabindex="0"> $x_{1} = \frac{- b - \sqrt{b^{2} - 4 a c}}{2 a}$

<mi>x</mi><mn>2</mn></msub><mo>=</mo><mfrac><mrow><mo>−</mo><mi>b</mi><mo>+</mo><msqrt><msup><mi>b</mi><mn>2</mn></msup><mo>−</mo><mn>4</mn><mi>a</mi><mi>c</mi></msqrt></mrow><mrow><mn>2</mn><mi>a</mi></mrow></mfrac></math>" role="presentation" tabindex="0"> $x_{2} = \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a}$

通过简单的加减就能得到

<mi>x</mi><mn>1</mn></msub><mo>+</mo><msub><mi>x</mi><mn>2</mn></msub><mo>=</mo><mo>−</mo><mfrac><mi>b</mi><mi>a</mi></mfrac></math>" role="presentation" tabindex="0"> $x_{1} + x_{2} = - \frac{b}{a}$

<mi>x</mi><mn>2</mn></msub><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub><mo>=</mo><mfrac><msqrt><msup><mi>b</mi><mn>2</mn></msup><mo>−</mo><mn>4</mn><mi>a</mi><mi>c</mi></msqrt><mi>a</mi></mfrac></math>" role="presentation" tabindex="0"> $x_{2} - x_{1} = \frac{\sqrt{b^{2} - 4 a c}}{a}$

<mi>x</mi><mn>1</mn></msub><msub><mi>x</mi><mn>2</mn></msub><mo>=</mo><mfrac><mi>c</mi><mi>a</mi></mfrac></math>" role="presentation" tabindex="0"> $x_{1} x_{2} = \frac{c}{a}$

(其中1，3式就是韦达定理）

或者将 y</mi><mo>=</mo><mi>a</mi><mrow class="MJX-TeXAtom-ORD"><mo>（</mo></mrow><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub><mo stretchy="false">)</mo><mo stretchy="false">(</mo><mi>x</mi><mo>−</mo><msub><mi>x</mi><mn>2</mn></msub><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $y = a （ x - x_{1}) (x - x_{2})$ 开括号

y</mi><mo>=</mo><mi>a</mi><msup><mi>x</mi><mn>2</mn></msup><mo>−</mo><mi>a</mi><mrow class="MJX-TeXAtom-ORD"><mo>（</mo></mrow><msub><mi>x</mi><mn>1</mn></msub><mo>+</mo><msub><mi>x</mi><mn>2</mn></msub><mo stretchy="false">)</mo><mi>x</mi><mo>+</mo><mi>a</mi><msub><mi>x</mi><mn>1</mn></msub><msub><mi>x</mi><mn>2</mn></msub></math>" role="presentation" tabindex="0"> $y = a x^{2} - a （ x_{1} + x_{2}) x + a x_{1} x_{2}$

也能对比出

b</mi><mo>=</mo><mo>−</mo><mi>a</mi><mo stretchy="false">(</mo><msub><mi>x</mi><mn>1</mn></msub><mo>+</mo><msub><mi>x</mi><mn>2</mn></msub><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $b = - a (x_{1} + x_{2})$

c</mi><mo>=</mo><mi>a</mi><msub><mi>x</mi><mn>1</mn></msub><msub><mi>x</mi><mn>2</mn></msub></math>" role="presentation" tabindex="0"> $c = a x_{1} x_{2}$

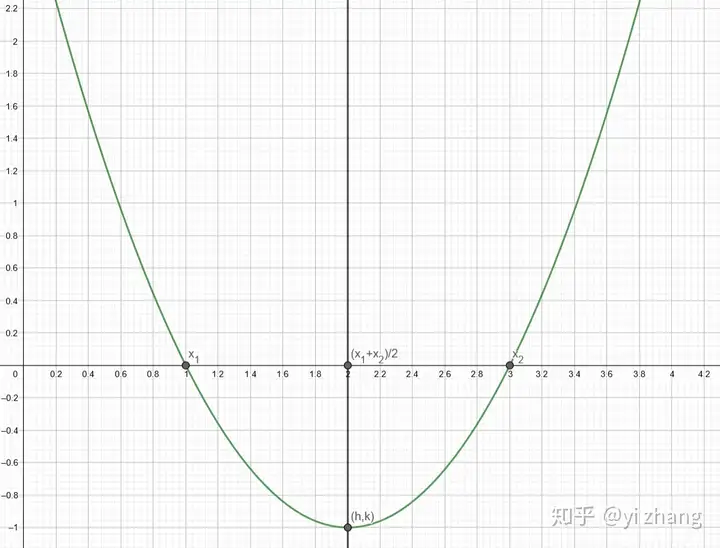
3. 顶点式和两根式

从上面的b</mi><mo>=</mo><mo>−</mo><mi>a</mi><mo stretchy="false">(</mo><msub><mi>x</mi><mn>1</mn></msub><mo>+</mo><msub><mi>x</mi><mn>2</mn></msub><mo stretchy="false">)</mo></math>" role="presentation" tabindex="0"> $b = - a (x_{1} + x_{2})$ 以及 h</mi><mo>=</mo><mo>−</mo><mfrac><mi>b</mi><mrow><mn>2</mn><mi>a</mi></mrow></mfrac></math>" role="presentation" tabindex="0"> $h = - \frac{b}{2 a}$

可以看出， h</mi><mo>=</mo><mfrac><mrow><msub><mi>x</mi><mn>1</mn></msub><mo>+</mo><msub><mi>x</mi><mn>2</mn></msub></mrow><mn>2</mn></mfrac></math>" role="presentation" tabindex="0"> $h = \frac{x_{1} + x_{2}}{2}$

当然也可以直观的从函数图形上得到。

二次函数的对称轴就是 <mi>x</mi><mn>1</mn></msub><mo>,</mo><msub><mi>x</mi><mn>2</mn></msub></math>" role="presentation" tabindex="0"> $x_{1}, x_{2}$ 连线的中点。

接下来对于顶点的纵坐标就并不那么直观了。

从代数上，我们观察下面两个式子。

能够发现 k</mi><mo>=</mo><mo>−</mo><mfrac><mrow><mi>a</mi><mo stretchy="false">(</mo><msub><mi>x</mi><mn>2</mn></msub><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub><msup><mo stretchy="false">)</mo><mn>2</mn></msup></mrow><mn>4</mn></mfrac></math>" role="presentation" tabindex="0"> $k = - \frac{a (x_{2} - x_{1})^{2}}{4}$

也就是k等于a/4*两根之间距离的平方的相反数。

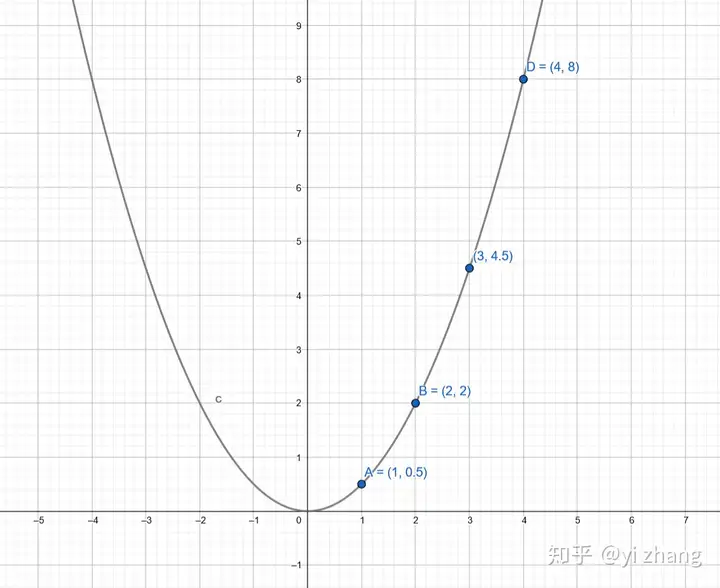
我们也可以从几何上直观的看出来

还是以y</mi><mo>=</mo><msup><mi>x</mi><mn>2</mn></msup><mo>−</mo><mn>4</mn><mi>x</mi><mo>+</mo><mn>3</mn></math>" role="presentation" tabindex="0"> $y = x^{2} - 4 x + 3$ 为例，

显然任意一个根到对称轴的距离为 <mrow><msub><mi>x</mi><mn>2</mn></msub><mo>−</mo><msub><mi>x</mi><mn>1</mn></msub></mrow><mn>2</mn></mfrac></math>" role="presentation" tabindex="0"> $\frac{x_{2} - x_{1}}{2}$ ，因为抛物线任意平移形状不变。也就是我可以将任意抛物线平移后得到形如 y</mi><mo>=</mo><mi>a</mi><msup><mi>x</mi><mn>2</mn></msup></math>" role="presentation" tabindex="0"> $y = a x^{2}$ ，例如 y</mi><mo>=</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><msup><mi>x</mi><mn>2</mn></msup></math>" role="presentation" tabindex="0"> $y = \frac{1}{2} x^{2}$ ,

横纵坐标保持着，纵坐标=1/2*横坐标的平方关系

而其实这种平方关系存在于任意的抛物线，只要是对称轴上点就有的性质，即使和x轴没有交点，取一个尽可能大的数值，总能和抛物线相交两点。

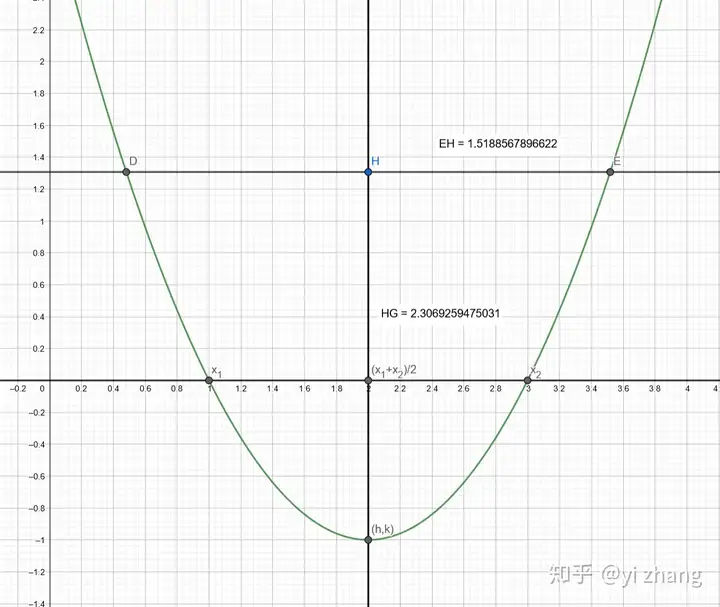
我在对称轴上取一点H （对于这开口向上的抛物线，H点要在顶点上方）过H做直线平行x轴，交抛物线于D，E两点。

任意移动H点，可以发现 H</mi><mi>G</mi><mo>≡</mo><mi>E</mi><msup><mi>H</mi><mn>2</mn></msup></math>" role="presentation" tabindex="0"> $H G \equiv E H^{2}$

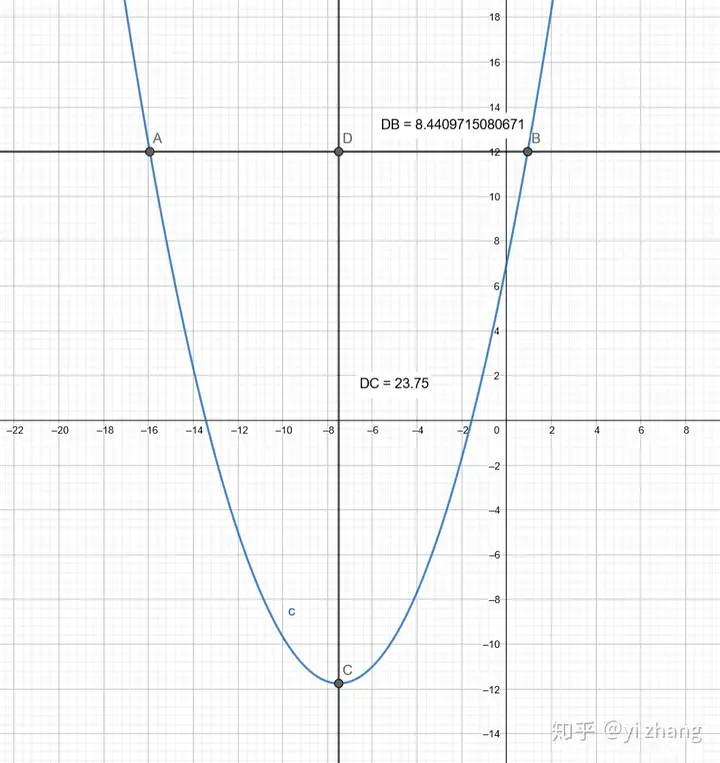
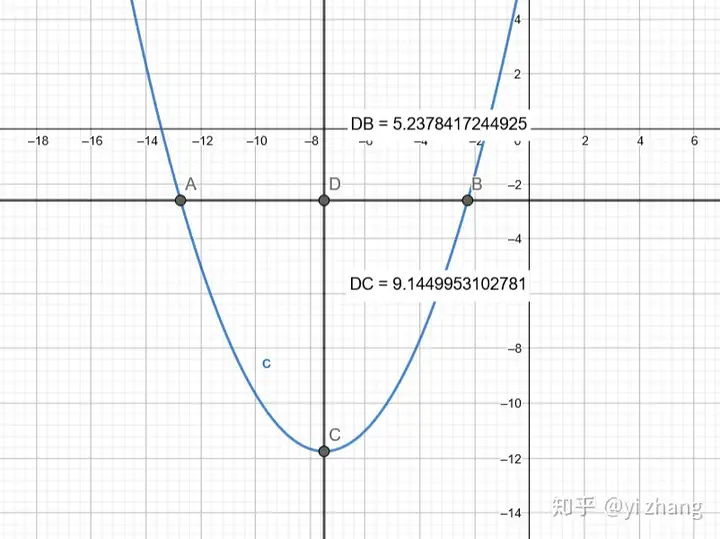
在来一个 a</mi><mo>≠</mo><mn>1</mn></math>" role="presentation" tabindex="0"> $a \neq 1$ 的二次函数试下。

比如 y</mi><mo>=</mo><mfrac><mn>1</mn><mn>3</mn></mfrac><msup><mi>x</mi><mn>2</mn></msup><mo>+</mo><mn>5</mn><mi>x</mi><mo>+</mo><mn>7</mn></math>" role="presentation" tabindex="0"> $y = \frac{1}{3} x^{2} + 5 x + 7$

当BD=8.44时候，DC=23.75=8.44*8.44/3

当BD=5.24时候，DC=9.14=5.24*5.24/3

上述总结，对于任意抛物线来说，抛物线上点的到对称轴的距离的平分*a=这个点和顶点之间的纵坐标之差。
(责任编辑：admin)

搜索

热门标签:

2023年初中数学二次函数基本概念和图像上特殊点