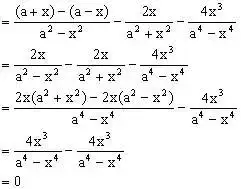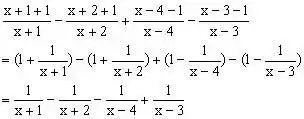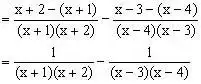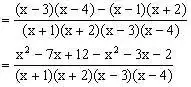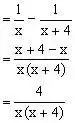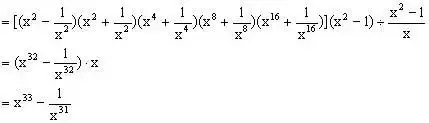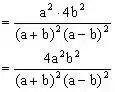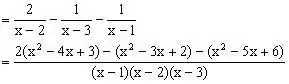');
(window.slotbydup=window.slotbydup || []).push({
id: '8096091',
container: s,
size: '580,90',
display: 'inlay-fix'
});
})();
分式运算的一般方法就是按分式运算法则和运算顺序进行运算。但对某些较复杂的题目,使用一般方法有时计算量太大,导致出错,有时甚至算不出来,下面列举几例介绍分式运算的几点技巧。
一、分段分步法
例1、计算:
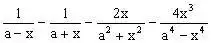
分析:若一次通分,计算量太大,注意到相邻分母之间,依次通分构成平方差公式,采用分段分步法,则可使问题简单化。
解:原式
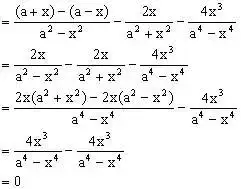
二、分裂整数法
例2、计算:
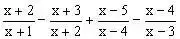
分析:当算式中各分式的分子次数与分母次数相同次数时,一般要先利用分裂整数法对分子降次后再通分;在解某些分式方程中,也可使用分裂整数法。
解:原式
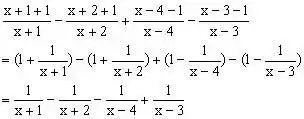
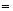
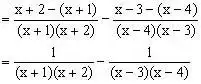
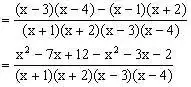
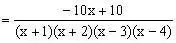
三、拆项法
例3、计算:
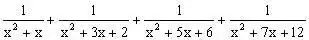
分析:对形如上面的算式,分母要先因式分解,再逆用公式
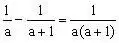
,各个分式拆项,正负抵消一部分,再通分。在解某些分式方程中,也可使用拆项法。
解:原式
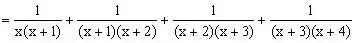
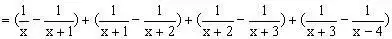
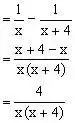
四、活用乘法公式
例4、计算:
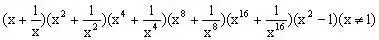
分析:在本题中,原式乘以同一代数式,之后再除以同一代数式还原,就可连续使用平方差公式,分式运算中若恰当使用乘法公式,可使计算简便。
解:当
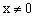
且
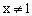
时,
原式
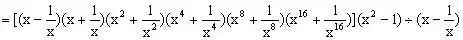
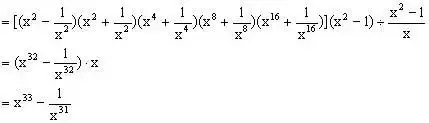
五、巧选运算顺序
例5、计算:
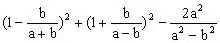
分析:此题若按两数和(差)的平方公式展开前后两个括号,计算将很麻烦,一般两个分式的和(差)的平方或立方不能按公式展开,只能先算括号内的。
解:原式
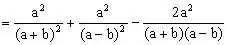
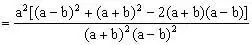
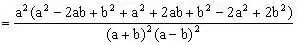
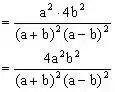
六、见繁化简
例6、计算:
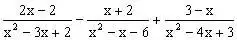
分析:若运算中的分式不是最简分式,可先约分,再选用适当方法通分,可使运算简便。
解:原式
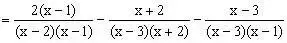
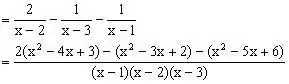
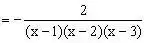
(责任编辑:admin) |