');
(window.slotbydup=window.slotbydup || []).push({
id: '8096091',
container: s,
size: '580,90',
display: 'inlay-fix'
});
})();
初中几何中,三角形内接四边形是经常考到的题型,一般是内接平行四边形、矩形、正方形等,常规思路是把要求的边长x设出来,利用相似三角形,构造关于x的方程,从而求出x的值。
例题:
如图,△ABC内接正方形DEFG,△AGF、△FEC、△BDG的面积分别是1、1、3,则正方形DEFG的边长为 _
(视频讲解在文末)
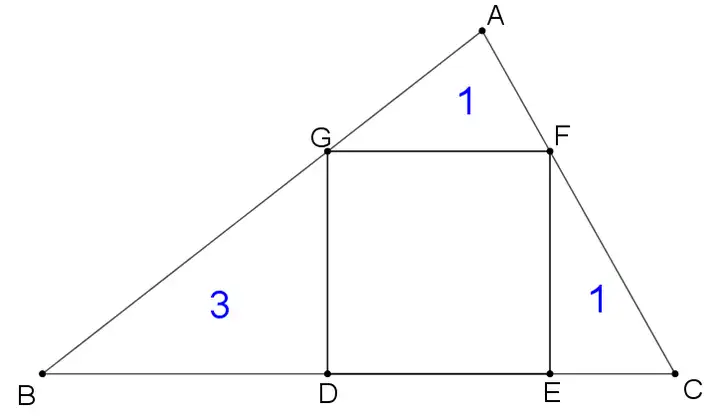
分析:按照常规思路,把正方形边长设为x,利用△AGF∽△ABC,高之比等于边长之比,构建关于x的方程解出x的值。
所以,
GF=x
BD=6/x
DE=x
EC=2/x
现在已经得到GF和BC的长,还需要另外一组对应边或者对应高之比。
题目中,△AGF的面积=△EFC的面积,GF=EF,可以得到△AGF中GF边上的高等于EC=2/x 。

那就可以利用△AGF∽△ABC,高之比等于GF与BC之比,构建关于x的方程求解。

现在讲解一下秒杀方法,对于三角形内接平行四边形问题,平行线分割成的三部分面积有一个等量关系。

感兴趣的同学思考下如何证明!
(提示:相似三角形面积之比等于相似比的平方)
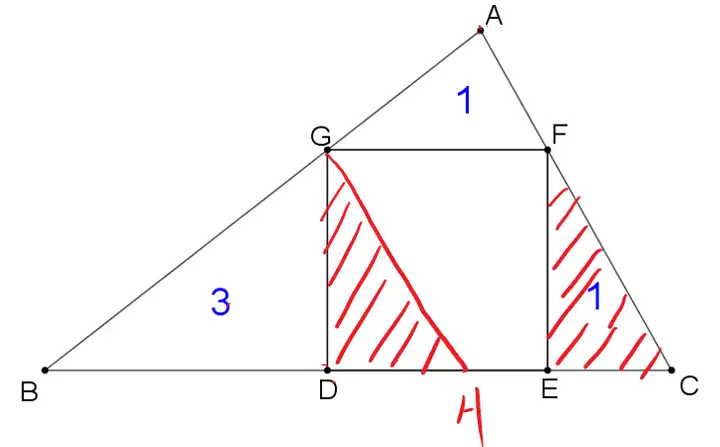
这个题就可以采用上面介绍的方法秒杀。
过点G做GH平行AC,交BC边于点H
易证△GDH≌△FEC,
则△BGH的面积为1+3=4
平行四边形GHCF的面积=2×√(1×4)=4
正方形GDEF的面积=平行四边形GHCF的面积=4
所以正方形边长为2
(责任编辑:admin) |





