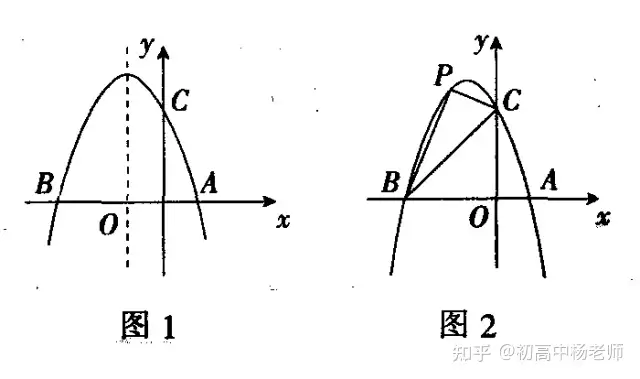
(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小?若存在，求出Q点的坐标;若不存在，请说明理由;(3)如图2，在(1)中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大?若存在，求出点P的坐标及△PBC的面积最大值;若没有，请说明理由。解答：(1)抛物线解析式为y=-x2-2x+3; (2)Q(-1，2);
    下面着重探讨求第(3)小题中面积最大值的几种方法.
    解法1
    补形、割形法
    几何图形中常见的处理方式有分割、补形等，此类方法的要点在于把所求图形的面积进行适当的补或割，变成有利于表示面积的图形。
    方法一如图3，设P点(x，-x2-2x+3)(-3
    

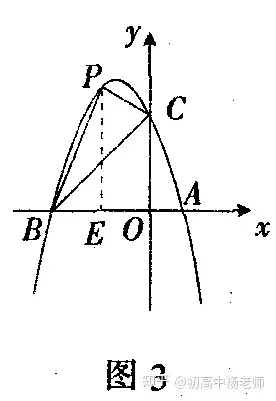
    方法二 如图4，设P点(x，-x2-2x+3)(-3
    

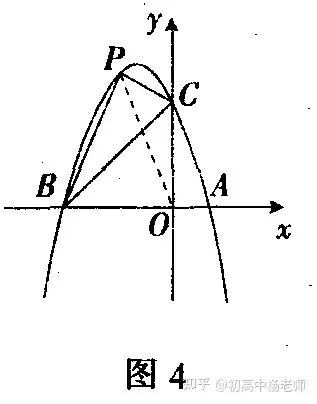
    (下略.)
    解法2
    “铅垂高，水平宽”面积法
    如图5，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”，我们可得出一种计算三角形面积的另一种方法：S△ABC=1/2ah，即三角形面积等于水平宽与铅垂高乘积的一半。
    

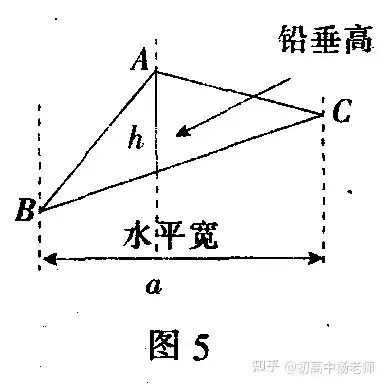
    根据上述方法，本题解答如下：解 如图6，作PE⊥x轴于点E，交BC于点F.
    

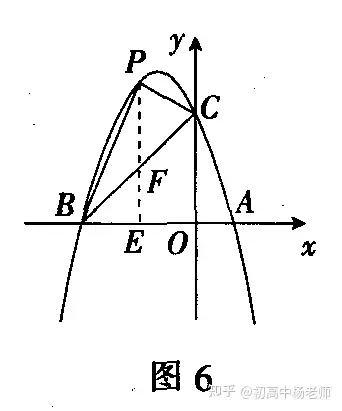
    设P点(x，-x2-2x+3)(-3
    

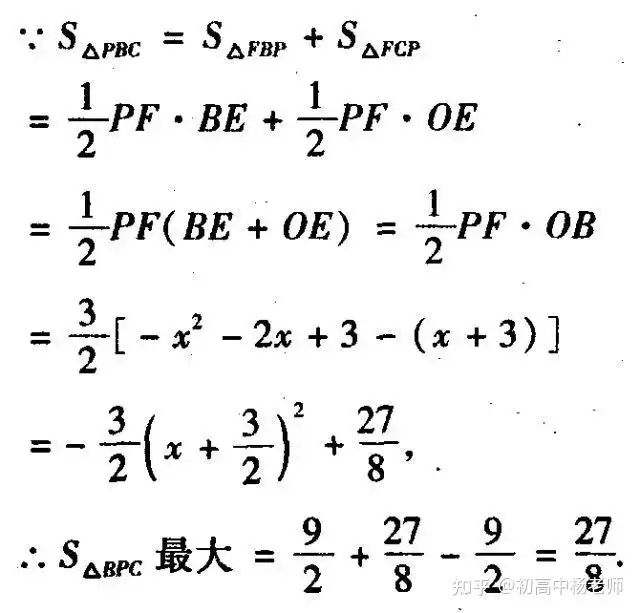
    ∴点P坐标为(-3/2，15/4)
    解法3
    切线法
    若要使△PBC的面积最大，只需使BC上的高最大.过点P作BC的平行线l，当直线l与抛物线有唯一交点(即点P)时，BC上的高最大，此时△PBC的面积最大，于是，得到下面的切线法。解 如图7，直线BC的解析式是y=x+3，过点P作BC的平行线l，从而可设直线l的解析式为：y=x+b.
    

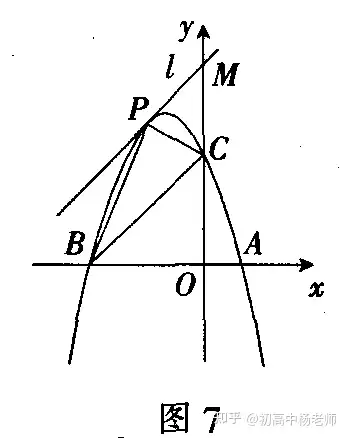
    =27/8
    解法4
    三角函数法
    本题也可直接利用三角函数法求得.解 如图8，作PE⊥x轴交于点E，交BC于点F，作PM⊥BC于点M.
    

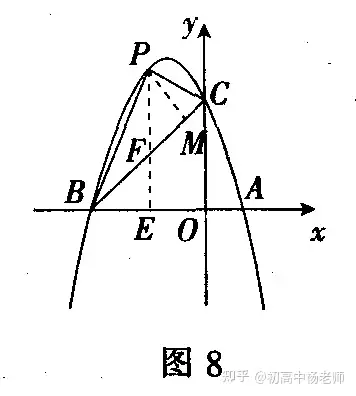
    设P点(x，-x2-2x+3)(-3
    则F(x，x+3).
    

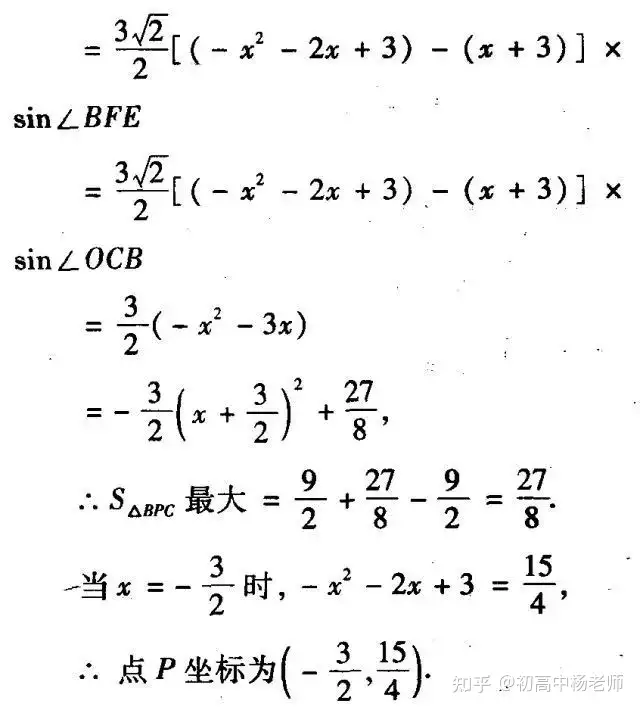
    从以上四种解法可以看到，本题解题思路都是过点P作辅助线，然后利用相关性质找出各元素之间的关系进行求解。
    

     (责任编辑：admin)