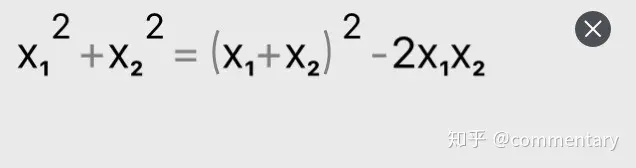
②
    

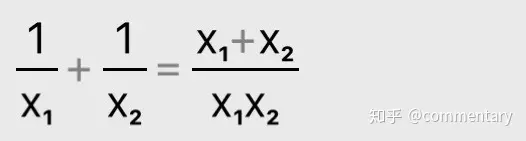
    ③
    

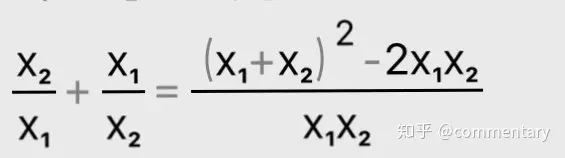
    ④
    

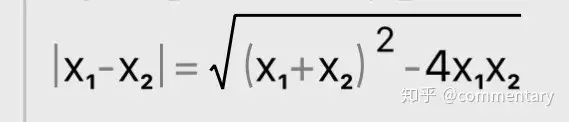
    ⑤
    

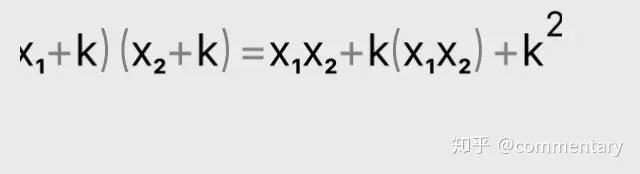
    最左边是x1
    这里强烈推荐photomath，可以进行数学运算也可绘出函数图像。
    二.不等式
    不等式符号若相同两式可加减。
    如：a+b>c 且e+f>d
    则a+b+e+f>c+d
    二次单项不等式可转化成二次函数进行求解。
    如x²-2-8<0
    ①确定函数图像
    

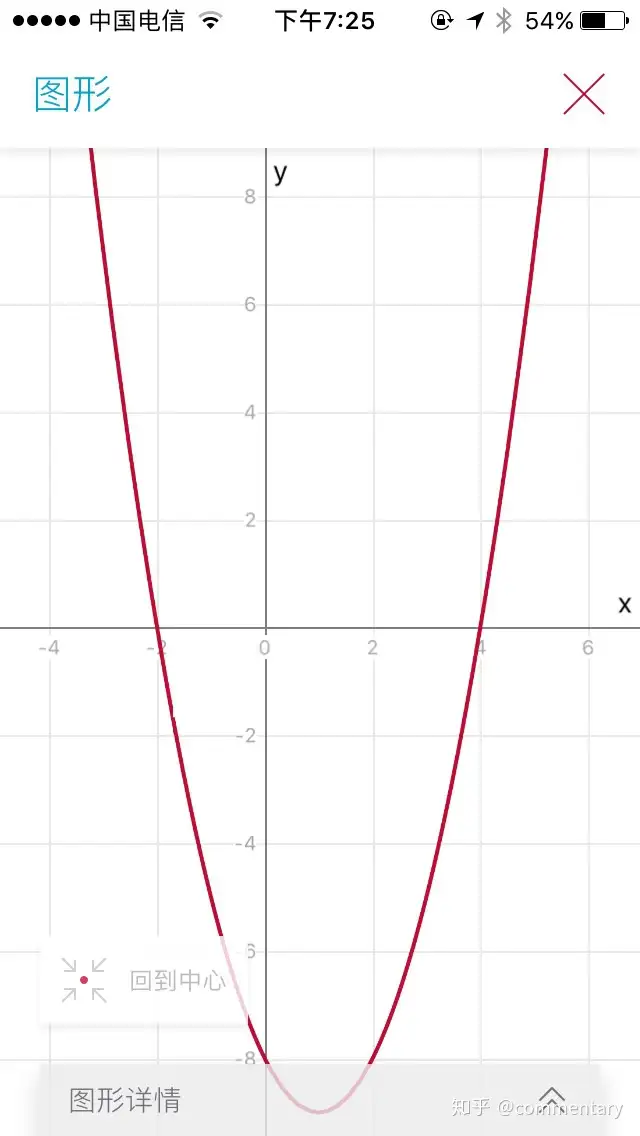
    用的是上面的那个APP
    ②通过函数图像可知函数图像开口向上当x的值为-2与4时函数值为0则当函数值小于0x的取值范围为-2<<4
    若有绝对值的不等式则要分类讨论。
    如│x+5│+│x-7│<0
    ①确定当x=-5，x=7为三区域的分界点
    

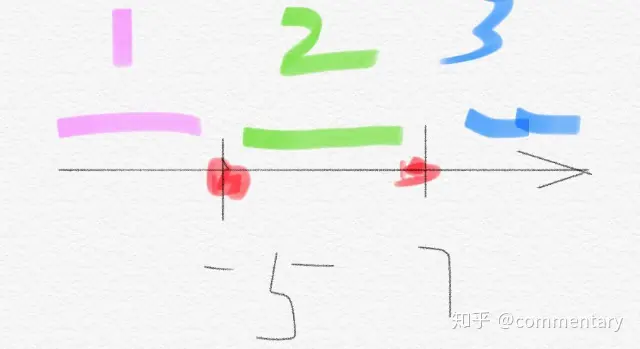
    ①当x<-5时│x+5│<0且│x-7│<0去绝对值后进行计算
    ②当-50而│x-7│<0去绝对值后进行计算
    ③当x>7时│x+5│>0且│x-7│>0去绝对值后进行计算
    综上所述通过计算无解
    分式不等式可将分子与分母相乘于是转化为函数进行求解同上。相乘后其实只要确定开口画出简略函数图像使分子分母分别等于0即为函数图像与x轴的交点就可以确定不等式取值范围(若分式后加了一个整式则将它转化为一个分式)。
    ★蛇形穿根法解不等式
    ◎适用于几个因式相乘的不等式。画出数轴，取每个因式等于0时未知数的值标在数轴上若开口向上从上穿，开口向下从下穿。因式次数为奇穿为偶不穿(奇穿偶不穿)
    

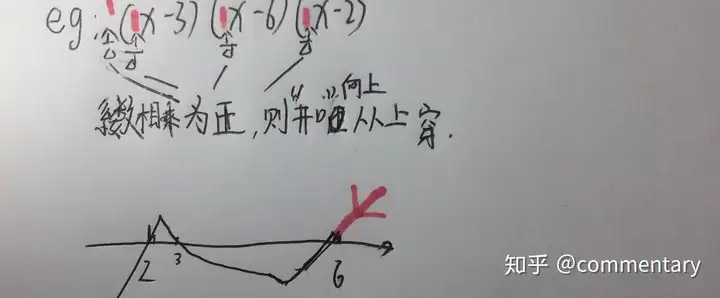
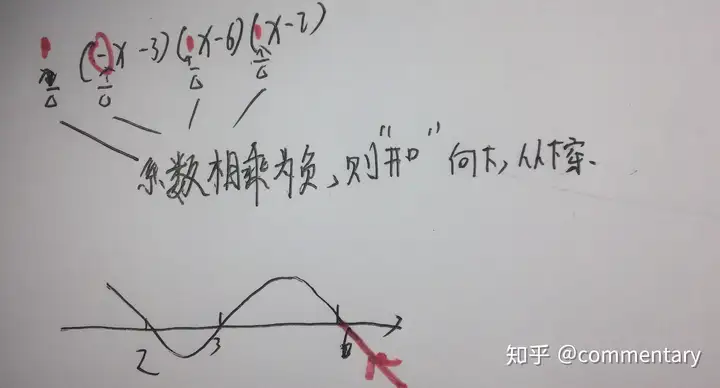
    再通过图像判断取值范围
    (ps：因式内降幂排列)
    三.公式
    ①中点坐标公式：已知点(x1,y1),(x2,y2)则有两点所连直线中点坐标为
    

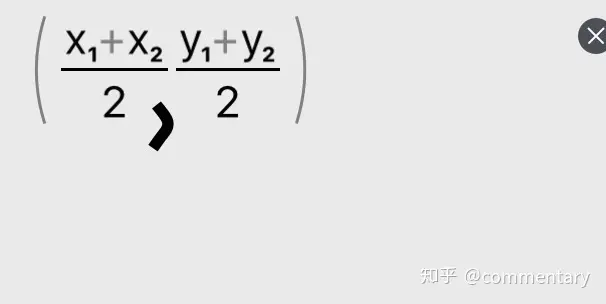
    ②求已知点(x,y)关于对称轴直线x=a的对应点为(2a-x,y)
    ③平面上n条直线最多有1/2(n-1)个交点
    ④基本比例式
    若：
    

    则ac=bd
    ⑤合分比
    若：
    

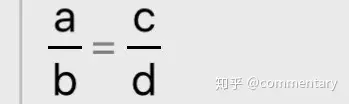
    则：
    

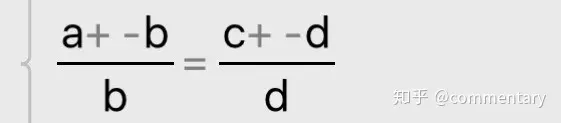
    ⑥等比：
    若：
    

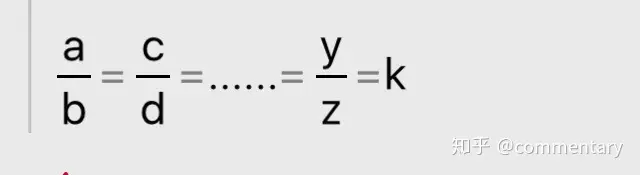
    则：
    

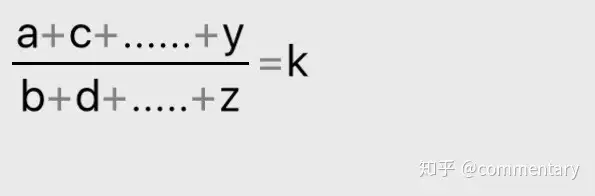
    四.均值不等式(常用于物理功率最值问题)：
    若a、b均是正实数,则：a+b≥2√(ab),当且仅当a=b时取等号.
    (一正二定三相等)
     (责任编辑：admin)