|
错解:∠1=∠2. 理由如下: 在△AOB和△DOC中,因为AB=DC,OA=OD,∠AOB=∠DOC, 所以△AOB≌△DOC,所以∠1=∠2. 分析:不存在“角角角(AAA)”和“边边角(SSA)”的判定方法,即对于一般三 角形,“有三个角对应相等的两个三角形不一定全等”和“有两边和其中一边的对角对应相等的两个三角形不一定 全等.” 正解:在△AOB和△DOC中,因为AB=DC,∠A=∠D,OA=OD, 所以△AO B≌△DOC(SAS),所以∠1=∠2. 3.不理解“对应”致误 例3、已知在两个直角三角形中,有一对锐角相等,又有一组边相等,那么这两个三角形是否全等? 错解:这两个三角形全等. 分析:对“ASA”全等判定法中“对应边相等”没有理解,错把边相等当成对应边相等. 正解:这两个三角形不一定全等. 如图4所示,在RT△EDC中,∠1=∠2,CD=AB,∠C=∠C=90°,显然△ABC和△EDC不全等. 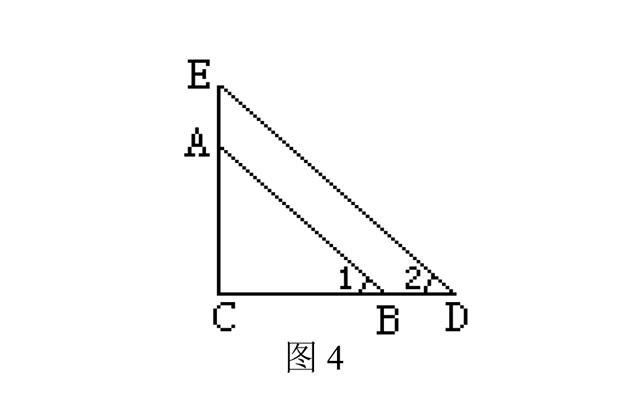 (责任编辑:admin) |
