|
2005全国课程改革实验区初中毕业学业考试数学学科试题评价报告十四 四、试题对教与学的启示 学业考试试题有两大作用,一是测量学生的数学学习水平与能力,二是它深刻地影响着今后的数学教学.下面就对今年数学学业考试试题对数学教学的影响作一些分析.这里的分析将从试题立意、求解策略、教学启示等角度进行. 试题立意是命题者为体现学业考试命题的指导思想、实现考查目标所确定的命题意向,它通常表现为三个方面:(1)以知识立意为主来选材与构思,着重考查知识的达成情况;(2)以能力立意为主来选材与构思,着重考查学生的能力水平;(3)以情感立意为主来选材与构思,着重考查学生的数学态度.随着数学学业考试命题改革的不断深入,传统的以知识立意为主的单一命题思路,已逐步让位于统筹考虑知识、能力与情感三方面,以能力立意为主的命题目标.求解策略是一种比解题技巧高出一筹的、对解题有重要启示与指导作用的思想与方法,掌握解题策略对提高解题能力大有帮助.教学启示是由试题所引发的一些关于数学教学的一些思考和对数学教学所提出的一些建议,这几个方面从不同角度揭示了试题对数学教学的启示作用. (一) 加强对数学内容的理解,有利于促进学生对数学知识与技能的掌握 数学学习在很大程度上是一种理解性学习,只有在理解的基础上,才有可能把所学数学知识运用到新的情境中,并灵活地运用它们来完成解决问题的任务.因此,关于理解方面的考查自然成了数学学业考试中所关注的一个重要内容,一方面考查学生对《课程标准》中所要求的知识内容的理解和掌握情况,一方面引导教学关注理解,由“重模仿”向“重理解”方向转变,促进学生扎实双基,发展能力. 例1(徐州)已知一次函数y=ax+b(a、b是常数),x与y的部分对应值如下表:
那么方程ax+b =0的解是 ;不等式ax+b>0的解集是 . 【试题立意】本题以一次函数为素材,以表格形式给出自变量与因变量的对应关系,着重考查对函数与方程、不等式之间的关系的理解水平. 【求解策略】由两点画出一次函数的图象,再由表格确定一元一次方程的解,由图象确定一元一次不等式的解. 【相近试题】若将一次函数换成二次函数,把确定一次方程的解改为确定解的范围,就可编出下题(2005年浙江省学业考试题): 根据下列表格的对应值:
判断方程 A、3<x<3.23 B、3.23<x<3.24 C、3.24<x<3.25 D、3.25 <x<3.26 若果不以表格的形式出现,而是直接以图象形式呈现,同时结合图象来确定函数的解析式,在此基础上进一步设置问题,就可以编拟出下面的试题(江西省学业考试题) 如图,直线L1、L2相交于点A, 根据图象解答下列问题: ⑴求出直线L2的函数关系式; ⑵当x在何范围时,两个函数的函数值都大于0? 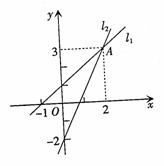 【教学启示】上面三道试题虽然表现形式有些不同,但本质上都是考查函数与方程、不等式之间的关系.函数与方程、不等式之间的关系是“数与代数”中的重要内容,用函数的观点来看待方程与不等式的解,不仅形象直观,而且可以更深刻地把握他们之间的内在联系,这种着眼于研究不同内容之间的联系是一种重要的数学方法与学习方法,应当高度重视.教学过程中,要让学生深刻地理解这一联系,就应当多让经历若干具体的画图、思考与讨论过程,否则,单靠讲解是难以达到目的的. 另一方面,将相似的试题放在一起进行比较也是十分有益的.如例1和相近试题的第一题,虽然有相近之处,但也有较大差别:后者包含了用图象求方程近似值的方法,前者无.学生认清了异同,理解上就进了一步. 例2 (扬州)一只不透名的布袋中有三只小球(除颜色以外没有任何区别),分别是2个红球,3个白球和5个黑球,每次只摸出一只小球,观察后放回搅匀.在连续9次摸出的都是黑球的情况下,第10次摸出红球的概率是___________ 【试题立意】 本题以摸球背景来构造问题,着重考查学生对概率意义的理解,而不是简单意义下的代数计算. 【求解策略】根据概率的意义进行求解.因为每次摸球都是独立的,且属于摸后放回等可能的模型,因而相对于每一次摸球而言,其概率都是相同的,该事件可能发生的次数与总次数的比就是所求的概率. 【教学启示】 概率是课程标准新增的学习内容,本题在前九次的摸球情况下,要求学生求第10次摸球的概率,有一定的迷惑性,要掌握概率的概念,并利用它解决问题,必须对“等可能”和“独立性”有较清晰的理解.摸球是概率问题中的常见模型,真正把这个模型理解透了,就容易发现这个模型在实际中的种种表现,就能够顺利地解决一些实际中的问题.可见,理解概率问题中的某些模型是非常重要的.而要学生理解这一模型的真正意义,就应当让学生在实验的基础上,进行讨论,以增加对问题的理解. 例3(南平市)学校请一位专家到校举办一次讲座,该专家备有4个专题,为确定讲哪一个专题学生更感兴趣,决定对学生进行调查,并对调查的数据进行处理,确定专家选讲专题的依据是调查后数据的( ) A.平均数 B.中位数 C.众数 D.方差 【试题立意】本题着重考查学生对统计中常见统计量(如平均数、中位数、众数、方差)的理解水平. 【求解策略】根据统计量(平均数、中位数、众数、方差)的意义,结合问题情景进行识别、确定.选B. 【相近试题】将试题情景作适当改变,就可编出其他的试题,如下面的试题(四川绵阳题): 从某市5000名初三学生中,随机地抽取100名学生,测得他们所穿鞋的鞋号(单位:公分)由小到大排列得到一个样本,则这个样本数据的平均数、中位数、众数和方差四个指标中,鞋厂最感兴趣的指标是( ) A.平均数 B.中位数 C.众数 D.方差 【教学启示】平均数、中位数、众数是用来刻画数据平均水平的统计量,方差、标准差是用来刻画数据波动情况的统计量,对于这些概念掌握情况的要求,重点不应放在概念的记忆与公式的计算方面,而应侧重于对这些概念的理解与运用,试题的设置就体现出了这一点.因此,在教学实践中,也可考虑设计一定的问题情景,让学生在处理具体问题时学会选择、运用适当的统计量,从而真正辨别、理解各统计量的区别与用途,达到真正掌握和正确运用的目的. 例4(北京市)如图所示,一根长2a的木棍AB,斜靠在与地面OM垂直的墙ON上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行. (1) 请判断木棍滑动的过程中,点P到点O的距离是否变化,并简述理由. (2) 在木棍滑动的过程中,当滑动到什么位置时,△AOB的面积最大?简述理由,并求出面积的最大值.  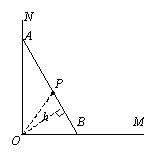 【试题立意】本题以梯子的滑动为背景来设置问题,着重考查学生对直角三角形模型的识别和直角三角形的性质的掌握情况. 【求解策略】通过观察发现问题中的几何模型.本问题中,当梯子滑动的过程中,墙面与地面保持着垂直关系,因而问题中隐含着一个直角三角形模型,当这个模型被发现后,剩下的问题就迎刃而解了. 【教学启示】发现问题情景中隐含的数学模型是本解决问题的关键所在.怎样才能发现这一模型呢?这需要在审视、理解情景的基础上,通过联想,识别出情景中隐藏的模型就是所熟悉的某种数学模型.这里熟悉已知的模型是基础,识别出问题中的模型是关键.这就告诉我们,一要设法让学生理解、掌握教材中常用数学模型,二要让学生经历识别、发现数学模型的活动,即要让学生参与观察、思考与交流等活动,以增强这方面的能力. (责任编辑:admin) |
