|
2010年广西贵港市中考数学试卷解析与点评 广西桂平市大洋中学 覃祖海 一、填空题(共10小题,每小题2分,满分20分) 1.计算:(﹣1)2= 1 . 考点:有理数的乘方。 专题:计算题。 分析:(﹣1)2表示2个﹣1相乘. 解答:解:原式=(﹣1)×(﹣1)=1. 点评:乘方是乘法的特例,乘方的运算可以利用乘法的运算来进行.负数的奇数次幂是负数,负数的偶数次幂是正数;﹣1的奇数次幂是﹣1,﹣1的偶数次幂是1. 2.2010年上海世博园区规划占地面积达5 280 000平方米,“5 280 000”用科学记数法表示为 5.28×106. 考点:科学记数法—表示较大的数。 专题:应用题。 分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于1时,n是正数;当原数的绝对值小于1时,n是负数. 解答:解:将5 280 000用科学记数法表示为5.28×106. 点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值. 3.在一次数学测试中,某小组5名学生的成绩(单位:分)如下:72、68、86、92、82.这组数据的中位数是 82 . 考点:中位数。 专题:应用题。 分析:求中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数. 解答:解:按从小到大排列这组数据:68,72,82,86,92.处于中间位置的那个数是82,那么由中位数的定义可知,这组数据的中位数是82.故答案为82. 点评:熟练掌握中位数的定义.中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数. 4.已知关于x的一元二次方程x2﹣bx+3=0的一个实数根为1,则b= 4 . 考点:一元二次方程的解。 分析:已知一元二次方程的一个实数根,可将其代入该方程中,即可求出b的值. 解答:解:∵一元二次方程x2﹣bx+3=0的一个实数根为1,∴1﹣b+3=0,即b=4. 点评:此题主要考查方程解的定义,所谓方程的解即能够使方程左右两边相等的未知数的值. 5.在四边形ABCD中,已知AD∥BC,若再添加一个条件,能使四边形ABCD成为平行四边形,则这个条件可以是 AD=BC .(写出一个条件即可,不用添加辅助线) 考点:平行四边形的判定。 专题:开放型。 分析:本题是开放题,可以针对平行四边形的判定方法,给出条件,再证明结论.答案可以有多种,主要条件明确,说法有理即可. 解答:解:添加条件AD=BC,可得出该四边形是平行四边形; ∵AD∥BC,AD=BC ∴四边形ABCD成为平行四边形.(一组对边平行且相等的四边形是平行四边形) 故答案为AD=BC(答案不唯一) 点评:解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论,挖掘它的内在联系,向“纵、横、深、广”拓展,从而寻找出添加的条件和所得的结论. 6.在一个不透明的口袋中,装有5个红球和n个黄球,它们除颜色不同外其余均相同.若从中随机摸出一个球,摸到黄球的概率为 考点:概率公式。 分析:根据口袋中装有5个红球和n个黄球,故球的总个数为5+n,再根据黄球的概率公式列式解答即可. 解答:解:∵口袋中装有5个红球和n个黄球,∴球的总个数为5+n,∵从中随机摸出一个球,摸到黄球的概率为 点评:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)= 7.如图所示,在梯形ABCD中,∠DCB=90°,CD∥AB,AB=25,BC=24,若将该梯形沿BD折叠,点C恰好与腰AD上的点E重合,则AE的长为 7 . 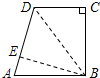 考点:梯形。 分析:根据题意,知BE是AD的垂直平分线,则BD=AB=25.根据勾股定理,得CD=7,则DE=AE=CD=7. 解答:解:根据折叠,得∠BED=∠C=90°,DE=CD.又AE=DE,∴BD=AB=25.根据勾股定理,得CD=7.则AE=DE=CD=7. 点评:此题综合运用了折叠的性质、线段垂直平分线的性质和勾股定理. 8.如图所示,AB为半圆O的直径,C、D、E、F是 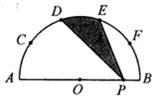 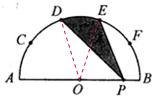 考点:扇形面积的计算。 分析:连接OD、OE,那么阴影部分的面积就等于扇形ODE的面积,根据C、D、E、F是弧AB的五等分点,可求得圆心角∠DOE的度数,进而可根据扇形的面积公式求出阴影部分的面积. 解答:解:连接OD、OE;∵C、D、E、F是 点评:此题主要考查的是扇形面积的计算方法,能够发现扇形ODE和阴影部分的面积关系是解决此题的关键. 9.如图所示,已知O是四边形ABCD内一点,OB=OC=OD,∠BCD=∠BAD=75°,则∠ADO+∠ABO= 135 度.  考点:多边形内角与外角;三角形的外角性质。 分析:由线段相等可得相应的角相等,那么可得∠CDO=∠DCO,∠OCB=∠OBC,可得这四个角的和;根据四边形ABCD的内角和为360°减去已知角的度数即为所求的度数. 解答:解:∵OB=OC=OD,∴∠CDO=∠DCO,∠OCB=∠OBC,∵∠DCO+∠BCO=75°,∴∠CDO+∠DCO+∠OCB+∠OBC=150°, ∴∠ADO+∠ABO=360°﹣∠BAD﹣(∠CDO+∠DCO+∠OCB+∠OBC)=135°. 点评:用的知识点为:等边对等角;四边形的内角和为360°. 10.阅读下列材料:当抛物线的解析式中含有字母系数时,随着系数中字母取值的不同,抛物线的顶点坐标也将发生变化.例如,由抛物线y=x2﹣2ax+a2+a﹣3,得到y=(x﹣a)2+a﹣3,抛物线的顶点坐标为(a,a﹣3),即无论a取任何实数,该抛物线顶点的纵坐标y和坐标x都满足关系式y=x﹣3.请根据以上的方法,确定抛物线y=x2+4bx+b顶点的纵坐标y和横坐标x都满足的关系式为y=﹣ 考点:待定系数法求二次函数解析式。 专题:阅读型。 分析:根据已知的叙述,即是把抛物线化为顶点式的形式,确定顶点坐标,根据横纵坐标的关系即可得到. 解答:解:y=x2+4bx+b=x2+4bx+4b2﹣4b2+b=(x+2b)2﹣4b2+b,因而抛物线的顶点坐标是:(﹣2b,﹣4b2+b),则﹣4b2+b=﹣(﹣2b)2﹣ 点评:本题主要是训练学生的读题,自学能力,正确题目中的已知条件是解决本题的关键. 二、选择题(共8小题,满分25分) 11.下列计算正确的是( ) A、a2?a3=a6 B、y3÷y3=y C、3m+3n=6mn D、(x3)2=x6 考点:同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方。 分析:根据同底数幂的运算法则、幂的乘方、合并同类项的法则进行计算即可. 解答:解:A、应为a2?a3=a5,故本选项错误;B、应为y3÷y3=1,故本选项错误;C、3m与3n不是同类项,不能合并,故本选项错误;D、(x3)2=x3×2=x6,正确.故选D. 点评:考查同底数幂的运算:乘法法则,底数不变,指数相加;除法法则,底数不变,指数相减;乘方,底数不变,指数相乘. 12.在平面直角坐标系中,点P的坐标为(﹣2,a2+1),则点P所在的象限是( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限 考点:点的坐标。 分析:先判断出点P的纵坐标的符号,再根据各象限内点的符号特征判断点P所在象限即可. 解答:解:∵a2为非负数,∴a2+1为正数,∴点P的符号为(﹣,+)∴点P在第二象限.故选B. 点评:本题考查了象限内的点的符号特点,注意a2加任意一个正数,结果恒为正数.牢记点在各象限内坐标的符号特征是正确解答此类题目的关键. 13.如图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何体的主视图是( ) 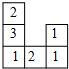 A、 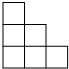 B、 B、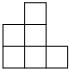 C、 C、 D、 D、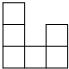 考点:简单组合体的三视图。 分析:俯视图中的每个数字是该位置小立方体的个数,分析其中的数字,得主视图右3列,从左到右分别是3,2,1个正方形. 解答:解:由俯视图中的数字可得:主视图右3列,从左到右分别是3,2,1个正方形.故选A. 点评:本题考查了学生的思考能力和对几何体三种视图的空间想象能力. 14.估计 A、在9﹣10之间 B、在10﹣11之间 C、在11﹣12之间 D、在12﹣13之间 考点:估算无理数的大小。 分析:先求它的平方,再看在哪两个整数之间,从而得到答案. 解答:解:∵121<138<144,∴11< 点评:此题主要考查了无理数的估算能力,现实生活中经常需要估算,估算应是我们具备的数学能力,“夹逼法”是估算的一般方法,也是常用方法. 15.甲、乙、丙、丁四人进行射击测试,每人射击8次,射击成绩的平均环数相同,方差分别为:S甲2=6.5,S乙2=5.3,S丙2=5.8,S丁2=8.1,则成绩最稳定的是( ) A、甲 B、乙 C、丙 D、丁 考点:方差。 分析:根据方差是用来衡量一组数据波动大小的量,故由甲乙丙丁的方差可作出判断. 解答:解:由于S乙2<S丙2<S甲2<S丁2,则成绩较稳定的同学是乙.故选B. 点评:本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定. 16.如图所示,在4×8的矩形网格中,每个小正方形的边长都为1,△ABC的三个顶点都在格点上,则tan∠BAC的值为( ) 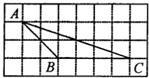 A、 考点:锐角三角函数的定义。 专题:网格型。 分析:找到∠ABC所在的直角三角形,进而求得∠BAC的对比与邻边之比即可. 解答:解:由勾股定理可得∠BAC所在的直角三角形的两条直角边为 点评:一个角的正切值等于这个角所在的直角三角形的对边与邻边之比;难点是得到∠BAC所在的直角三角形的两条直角边长度. 17.如图所示,在对角线长分别为12和16的菱形ABCD中,E、F分别是边AB、AD的中点,H是对角线BD上的任意一点,则HE+HF的最小值是( )   A、14 B、28 C、6 D、10 考点:轴对称-最短路线问题;菱形的性质。 专题:计算题;几何综合题。 分析:要求HE+HF的最小值,HE、HF不能直接求,可考虑通过作辅助线转化HE、HF的值,从而找出其最小值求解. 解答:解:如图: 作EE′⊥BD交BC于E′,连接E′F,则E′F就是HE+HF的最小值,∵E、F分别是边AB、AD的中点,∴E′F 点评:考查菱形的性质和轴对称及平行四边形的判定等知识的综合应用. 18.如图所示,A(﹣   A、 考点:坐标与图形性质;等边三角形的性质;勾股定理。 分析:过P点作PD⊥x轴,垂足为D,根据A(﹣ 解答:解:过P点作PD⊥x轴,垂足为D, 由A(﹣ ∴S△ABC= 又S△ABP=S△AOB+S梯形BODP﹣S△ADP=  由2S△ABP=S△ABC,得 点评:本题考查了点的坐标与线段长的关系,不规则三角形面积的表示方法. 三、解答题(共8小题,满分76分) 19.(1)计算:  ; ;(2)先化简,再求值:  ,其中a=﹣ ,其中a=﹣考点:特殊角的三角函数值;分式的化简求值;零指数幂;负整数指数幂。 分析:(1)任何不等于0的数的0次幂都等于1,一个数的负整数次幂等于这个数的正整数次幂的倒数,cos45°= (2)首先对代数式进行化简,先算除法,即把除式的分子、分母颠倒相乘,再根据分式的加减法法则进行计算;然后代值计算. 解答:解:(1)原式=1+5﹣2× (2)原式=  = =当a=﹣ 点评:第(1)小题考查了幂运算的性质、特殊角的锐角三角函数值以及绝对值的化简; 第(2)小题考查了分式的混合运算,能够借助因式分解的知识,熟练进行约分. 20.已知点P(1,2)在反比例函数y= (1)当x=﹣2时,求y的值; (2)当1<x<4时,求y的取值范围. 考点:反比例函数图象上点的坐标特征。 专题:计算题。 分析:(1)把点P的坐标代入反比例函数解析式可得到比例系数k,然后把x=﹣2代入即可求得相应的函数值y;(2)把x=1,x=4代入函数关系式,得到对应的y的值,那么y的取值在这两个得到的值之间. 解答:解:(1)∵点P(1,2)在反比例函数y= 当x=﹣2时,y= 点评:用到的知识点为:点在函数解析式上,那么这点的横纵坐标应适合这个函数解析式;给定两个变量中的一个量,根据函数关系式可得另一个量. 21.某校为了了解九年级男生50米短跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分按A,B,C,D四个等级进行统计,并绘制成下面扇形图和统计表:  请你根据以上图表提供的信息,解答下列问题: (1)在统计表中x= 12 ,y= 2 ,m= 0.24 ,n= 0.04 ; (2)在扇形图中,A等级所对应的圆心角是 136.8 度; (3)如果该校九年级共有男生300名,试估计这300名男生中成绩等级没有达到A或B得共有多少人? 考点:频数(率)分布表;用样本估计总体;扇形统计图。 专题:阅读型。 分析:(1)通过观察扇形统计图以及频数分布表可知,B占40%,即20人,由统计表中B的人数可得x,继而得到m,y,n;(2)算出A的人数后,由圆心角和频数的关系可得答案; (3)由总数和频率的关系可得答案. 解答:解:(1)由通过观察扇形统计图以及频数分布表可知,B占40%,即50×40%=20人,所以x=20﹣8=12人;y=50﹣6﹣13﹣20﹣6﹣3=2人;m=12÷50=0.24;n=2÷50=0.04 (2)由表可知,A等级人数为19人,所以圆心角为360°× (3)由上表可知成绩等级没有达到A或B得共有6+2+3=11∴300× 答:估计这300名男生中成绩等级没有达到A或B得共有66人. 点评:本题难度中等,主要考查考生分析图表能力. 22.如图所示,把△ABC置于平面直角坐标系中,请你按下列要求分别画图: (1)画出△ABC向下平移5个单位长度得到的△A1B1C1; (2)画出△ABC绕着原点O逆时针旋转90°得到的△A2B2C2; (3)画出△ABC关于原点O对称的△A3B3C3.  考点:作图-旋转变换;作图-平移变换。 专题:作图题。 分析:(1)分别将A、B、C三点向下平移5个单位,得点A1、B1、C1,顺次连接这三点即可得所求作的三角形.(2)把握好旋转的三个要点,按要求作图即可;旋转中心:点O,旋转方向:逆时针方向,旋转角度:90°.(3)分别作A、B、C关于原的对称点A3、B3、C3,然后顺次连接这三点即可. 解答:解:如图所示:  点评:此题考查的是平移、旋转变换、中心对称的作图方法,熟练掌握各种几何变换的特点是解答此类问题的关键. 23.如图所示,在△ABC中,AB=AC,D为AB上一点,E为AC延长线上的一点,且CE=BD,连接DE交BC于点P. (1)求证:PE=PD (2)若CE:AC=1:5,BC=10,求BP的长.  考点:全等三角形的判定与性质;等腰三角形的性质。 专题:计算题;证明题。 分析:(1)过点D作DF∥AC交BC于点F,由等腰三角形性质和平行线性质可得∠DBF=∠DFB,可推得DB=DF,由因为已知CE=BD,即可得DF=CE,通过AAS可得△DFP≌△ECP,即得到PE=PD.(2)由已知条件易证得△BDF∽△BAC,且 解答:解:(1)证明:过点D作DF∥AC交BC于点F,∴∠ACB=∠DFB∠FDP=∠E,∵AB=AC(已知),∴∠ACB=∠ABC,∴∠ABC=∠DFB,∴DF=DB;又∵CE=BD(已知),∴CE=DF;又∵∠DPF=∠CPE,∴△ECP≌△DFP,∴PE=PD; (2)∵CE=BD,AC=AB,CE:AC=1:5(已知),∴BD:AB=1:5,∵DF∥AC,∴△BDF∽△BAC, ∴ 点评:本题主要考查全等三角形全等的判定与性质及等腰三角形的性质;涉及到相似三角形、等腰三角形等知识点,是一道综合题型,正确作出辅助线是解题的关键. 24.某儿童服装店欲购进A、B两种型号的儿童服装,经调查:B型号童装的进货单价是A型号童装进货单价的2倍,购进A型号童装60件和B型号童装40件共用2100元. (1)求A、B两种型号童装的进货单价各是多少元? (2)若该店每销售1件A型号童装可获利4元,每销售1件B型号童装可获利9元,该店准备用不超过6300元购进A、B两种型号童装共300件,且这两种型号童装全部售出后总获利不低于1795元,问应该怎样进货,才能使总获利最大,最大获利为多少元? 考点:一元一次不等式组的应用;一元一次方程的应用。 分析:第(1)题,由题目中B型号童装的进货单价是A型号童装进货单价的2倍,可设A型号童装进货单价为x元,则B型号童装进货单价为2x元,再利用购进A型号童装60件和B型号童装40件共用2100元.可列方程:60x+40×2x=2100进行解答. 第(2)题,由题意可知:①购进A、B两种型号童装共300件的支出≤6300元,②两种型号童装全部售出后总获利≥1795元.故可设该店购进A型号童装a件,购进B型号童装(300﹣a)件,得不等式组:  解之得:180≤a≤181;获得利润=4a+9(300﹣a)=2700﹣5a,即最大获利与a的大小有关系,于是据a的取值,最大获利问题解决. 解之得:180≤a≤181;获得利润=4a+9(300﹣a)=2700﹣5a,即最大获利与a的大小有关系,于是据a的取值,最大获利问题解决.解答:解:(1)设A型号童装进货单价为x元,则B型号童装进货单价为2x元,由题意得:60x+40×2x=2100,解之得:x=15,则2x=30. 答:A、B两种型号童装的进货单价分别是15元、30元. (2)设该店购进A型号童装a件,则购进B型号童装(300﹣a)件,由题意得:  ,解之得:180≤a≤181. ,解之得:180≤a≤181.设总获利润为W元,则:W=4a+9(300﹣a)=2700﹣5a,于是W是关于a的一次函数,a越小则W越大,故当a=180时,W最大,最大W=2700﹣5×180=1800,于是:300﹣a=120. 答:该店应购进A型号童装180件,B型号童装120件,才能使总获利最大,最大总获利为1800元. 点评:一元一次不等式组的应用问题的解答关键是审题,找出题干中的相等关系和不等关系,设未知数,列关系式解答. 25.如图所示,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是 (1)求证DM= (2)求证:直线PC是扇形OAB所在圆的切线; (3)设y=CD2+3CM2,当∠CPO=60°时,请求出y关于r的函数关系式.   考点:切线的判定;勾股定理。 专题:动点型。 分析:(1)连接OC,由CD⊥OA于点D,CE⊥OB于点E,证明四边形ODCE是矩形,(2)设OC与DE交于点F,则在矩形ODCE中,FC=FD,根据角的关系得到PC⊥OC于点C,(3)过C作CH⊥DE于点H,在Rt△OCD和Rt△CDH中解得CD、DH、CH,进而写出y关于r的函数关系式. 解答:解:(1)证明:连接OC,∵点C是 又∵DM=2EM,∴DM= (2)设OC与DE交于点F,则在矩形ODCE中,FC=FD,∴∠CDE=∠DCO,又∵∠CPD+∠PCD=90°,∠CPD=∠CDE,∴∠DCO+∠PCD=90°,即PC⊥OC于点C,又∵OC为扇形OAB的半径,∴PC是扇形OAB所在圆的切线; (3)过C作CH⊥DE于点H,∵∠OCD=∠CDH=∠CPO=60°,∴在Rt△OCD和Rt△CDH中,得CD= ∴在Rt△CMH中,得CM2=MH2+CH2= 则y=CD2+3CM2= 点评:本题考查了切线的判定,勾股定理等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可. 26.如图所示,已知直线y=kx﹣1与抛物线y=ax2+bx+c交于A(﹣3,2)、B(0,﹣1)两点,抛物线的顶点为C(﹣1,﹣2),对称轴交直线AB于点D,连接OC. (1)求k的值及抛物线的解析式; (2)若P为抛物线上的点,且以P、A、D三点构成的三角形是以线段AD为一条直角边的直角三角形,请求出满足条件的点P的坐标; (3)在(2)的条件下所得的三角形是否与△OCD相似?请直接写出判断结果,不必写出证明过程.   考点:二次函数综合题。 专题:压轴题。 分析:(1)将点A的坐标代入直线AB的解析式中,即可确定k的值;根据A、B的坐标,可用待定系数法确定抛物线的解析式. (2)根据抛物线的解析式,易求得D点坐标,可得OB=OD,即△OBD是等腰直角三角形;若△PAD是以AD为直角边的直角三角形,那么可分两种情况: ①以D为直角顶点,过D作直线l1⊥AD,直线l1与抛物线的交点即为所求的P点,设直线l1与y轴的交点为E,由于△ODB是等腰直角三角形,故△ODE也是等腰直角三角形,即OD=OE,由此可得E点坐标,进而可根据D、E的坐标求出直线l1的解析式,联立抛物线的解析式,即可得P点坐标; ②以A为直角顶点,过A作直线l2⊥AD,同理直线l2与抛物线的交点也符合P点的要求,由于直线l1∥直线l2,根据直线l2的斜率和A点的坐标,即可求出直线l2的解析式,然后联立抛物线的解析式,可得P点的坐标. (3)根据C、D坐标,易得OC、CD的长,若(2)的直角三角形与△OCD相似,那么它们的直角边应该对应成比例,可先求出(2)中直角三角形的直角边长,然后再进行判断. 解答:解:(1)∵直线y=kx﹣1经过A(﹣3,2),∴把点A(﹣3,2)代入y=kx﹣1得: 2=﹣3k﹣1,∴k=﹣1,把A(﹣3,2)、B(0.,﹣1)、C(﹣1,﹣2)代入y=ax2+bx+c 得  ,∴ ,∴ ,∴抛物线的解析式为y=x2+2x﹣1. ,∴抛物线的解析式为y=x2+2x﹣1.(2)由  得D(﹣1,0),即点D在x轴上,且|OD|=|OB|=1, 得D(﹣1,0),即点D在x轴上,且|OD|=|OB|=1,∴△BDO为等腰直角三角形,∴∠BDO=45°, ①过点D作l1⊥AB,交y轴于E,交抛物线于P1、P2两点,连接P1A、P2A, 则△P1AD、△P2AD都是满足条件的直角三角形,∵∠EDO=90°﹣∠BDO=45°, ∴|OE|=|OD|=1,∴点E(0,1),∴直线l1的解析式为y=x+1, 由  解得: 解得: 或 或 , ,∴满足条件的点为P1(﹣2,﹣1)、P2(1,2); ②过点A作l2⊥AB,交抛物线于另一点P3,连接P3D,则△P3AD是满足条件的直线三角形, ∵l1∥l2且l2过点A(﹣3,2) ∴l2的解析式为y=x+5, 由  解得:  或 或 (舍去), (舍去),∴P3的坐标为(2,7), 综上所述,满足条件的点为P1(﹣2,﹣1)、P2(1,2)、P3(2,7), (3)∵P1(﹣2,﹣1),A(﹣3,﹣2),D(﹣1,0), ∴P1D= 而OC=1,CD=2,即P1D:AD=OC:CD, 又∵∠OCD=∠P1AD=90°, ∴△P1AD∽△OCD, 同理可求得△P2AD与△OCD不相似,△P3AD与△OCD不相似; 故判断结果如下: △P1AD∽△OCD, △P2AD与△OCD不相似; △P3AD与△OCD不相似. 点评:此题考查了用待定系数法确定函数解析式的方法、直角三角形的判定、函数图象交点坐标的求法、相似三角形的判定和性质等知识,(2)题中,一定要根据直角三角形的不同直角顶点分类讨论,以免漏解. (责任编辑:admin) |
