“三角板”与函数图象为背景的中考试题赏析
贵州省道真县玉溪镇中心学校 胡 军
三角板是学生学习数学的常用工具,一幅三角板,由于它的边和角的特殊性,蕴含丰富的数学知识,新课程实施以来,以三角板为背景的中考试题倍受命题者的青昧,大量出现在各地的中考试题中,本文拟从2011年中考试题中以三角板与函数图象为背景的试题加以分类赏析,与读者共享。
一、三角板与反比例函数图象的结合
例1:(金华)如图1,将一块直角三角板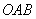 放在平面直角坐标系中, 放在平面直角坐标系中, , ,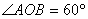 ,点 ,点 在第一象限,过点 在第一象限,过点 的双曲线为 的双曲线为 .在 .在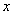 轴上取一点 轴上取一点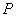 ,过点 ,过点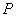 作直线 作直线 的垂线 的垂线 ,以直线 ,以直线 为对称轴,线段 为对称轴,线段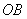 经轴对称变换后的像是 经轴对称变换后的像是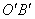 。 。
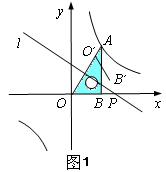
⑴当点 与点 与点 重合时,点 重合时,点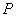 的坐标是 的坐标是
⑵设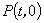 ,当 ,当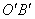 与双曲线有交点时, 与双曲线有交点时,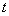 的取值范围是 。 的取值范围是 。
解析:⑴当点 与点 与点 重合时, 重合时, 垂直平分 垂直平分 ,则易知 ,则易知 ,点 ,点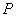 的坐标是 的坐标是 ; ;
⑵由图形的对称变换和含30°角的直角三角形的性质易得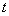 的取值范围是: 的取值范围是: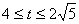 或 或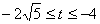 。 。
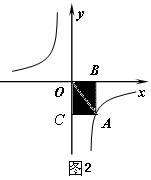
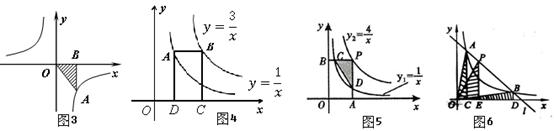
感悟:涉及反比例函数的问题,有一个非常实用的基本结论:如图2,从反比例函数 的图象上任意一点 的图象上任意一点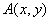 分别作 分别作 轴,垂足为 轴,垂足为 , ,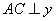 轴,垂足为 轴,垂足为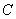 ,则矩形 ,则矩形 的面积= 的面积= 。这个基本结论揭示了反比例函数的本质(几何意义)。运用此结论,还可直接解决一些中考试题。 。这个基本结论揭示了反比例函数的本质(几何意义)。运用此结论,还可直接解决一些中考试题。
中考链接:
1.(鄂州)如图3:点 在双曲线 在双曲线 上, 上, ⊥轴于 ⊥轴于 ,且△ ,且△ 的面积S△AOB=2,则 的面积S△AOB=2,则 。 。
2.(孝感) 如图4,点 在双曲线 在双曲线 上,点 上,点 在双曲线 在双曲线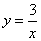 上,且 上,且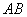 ∥ ∥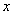 轴, 轴,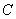 、 、 在 在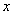 轴上,若四边形 轴上,若四边形 的面积为矩形,则它的面积为 . 的面积为矩形,则它的面积为 .
3.(遵义)如图5,已知双曲线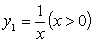 , ,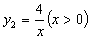 ,点 ,点 为双曲线 为双曲线 上的一点,且 上的一点,且 ⊥ ⊥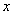 轴于点 轴于点 , ,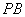 ⊥ ⊥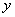 轴于点 轴于点 , , 、 、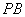 分别交双曲线 分别交双曲线 于 于 、 、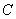 两点,则△ 两点,则△ 的面积为 。 的面积为 。
4.(东营)如图6,直线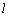 和双曲线 和双曲线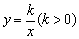 交于 交于 、 、 两点, 两点,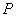 是线段 是线段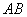 上的点(不与 上的点(不与 、 、 重合),过点 重合),过点 、 、 、 、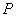 分别向 分别向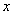 轴作垂线,垂足分别是 轴作垂线,垂足分别是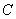 、 、 、 、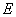 ,连结 ,连结 、 、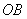 、 、 ,设△ ,设△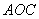 面积是 面积是 、△ 、△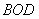 面积是 面积是 、△ 、△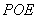 面积是 面积是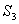 ,则( ) ,则( )
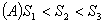 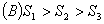 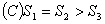 
答案:由反比例函数的几何意义易知:1,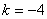 ;2,矩形 ;2,矩形 的面积等于2;3,△ 的面积等于2;3,△ 的面积为: 的面积为: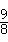 ; 4,应选 ; 4,应选 。 。
二、与二次函数(抛物线)的结合
例2:(株洲):孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线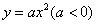 的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点 的性质时,将一把直角三角板的直角顶点置于平面直角坐标系的原点 ,两直角边与该抛物线交于 ,两直角边与该抛物线交于 、 、 两点,请解答以下问题: 两点,请解答以下问题:
⑴若测得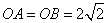 (如图7),求 (如图7),求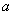 的值; 的值;
⑵对同一条抛物线,孔明将三角板绕点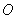 旋转到如图8所示位置时,过 旋转到如图8所示位置时,过 作 作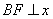 轴于点 轴于点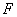 ,测得 ,测得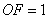 ,写出此时点 ,写出此时点 的坐标,并求点 的坐标,并求点 的横坐标; 的横坐标;
⑶对该抛物线,孔明将三角板绕点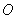 旋转任意角度时惊奇地发现,交点 旋转任意角度时惊奇地发现,交点 、 、 的连线段总经过一个固定的点,试说明理由并求出该点的坐标。 的连线段总经过一个固定的点,试说明理由并求出该点的坐标。

解析:⑴设线段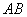 与 与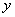 轴的交点为 轴的交点为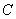 ,由抛物线的对称性可得 ,由抛物线的对称性可得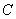 为 为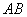 中点,又由三角板的特殊性可知, 中点,又由三角板的特殊性可知, 点的坐标为: 点的坐标为:  ( (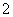 , ,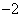 ), 将 ), 将 ( (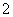 , ,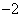 )代入抛物线 )代入抛物线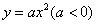 得, 得,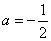 。 。
⑵此问解法较多,现举例如下:
如图8,过点 作 作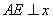 轴于点 轴于点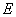 , ,
解法一:证△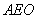 ∽△ ∽△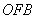 和抛物线的有关知识可求得点 和抛物线的有关知识可求得点 的横坐标; 的横坐标;
解法二:由解直角三角形和抛物线的有关知识可求得点 的横坐标; 的横坐标;
解法三:利用勾股定理和抛物线的有关知识可求得点 的横坐标。 的横坐标。
⑶解法一:设 ( (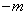 , ,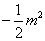 )( )(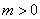 ), ), ( (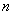 , ,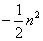 )( )(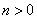 ), ),
设直线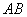 的解析式为: 的解析式为: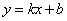 ,得 ,得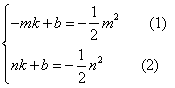 ,解得 ,解得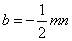 ,又易知△ ,又易知△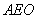 ∽△ ∽△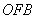 , , 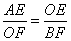 , , 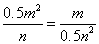 , ,  , ,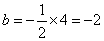 .由此可知不论 .由此可知不论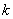 为何值,直线 为何值,直线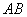 恒过点( 恒过点(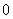 , ,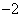 ) )
解法二:设 ( (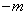 , ,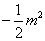 )( )(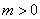 ), ), ( (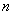 , ,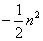 )( )(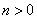 ),直线 ),直线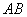 与 与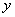 轴的交点为 轴的交点为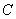 ,根据 ,根据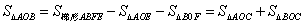 ,可得 ,可得
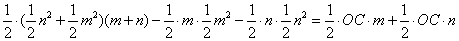 , ,
化简,得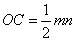 . 又易知△ . 又易知△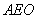 ∽△ ∽△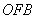 ,∴ ,∴ 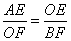 , ,
∴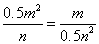 , ∴ , ∴ ,∴ ,∴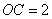 为固定值。故直线 为固定值。故直线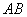 恒过其与 恒过其与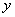 轴的交点 轴的交点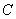 ( (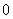 , ,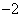 )。 )。
解法三: 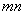 的值也可以通过以下方法求得: 的值也可以通过以下方法求得:
由前可知,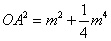 , ,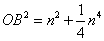 , , 由 由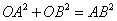 ,得: ,得: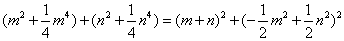 ,化简,得 ,化简,得 。 。
例3:(东营):在平面直角坐标系中,现将一块等腰直角三角板放在第一象限,斜靠在两坐标轴上,且点 (2,0),点 (2,0),点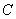 (1,0),如图9所示;抛物线 (1,0),如图9所示;抛物线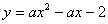 经过点 经过点 。 。
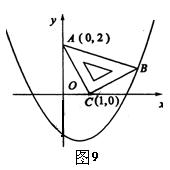
⑴求点 的坐标; 的坐标;
⑵求抛物线的解析式;
⑶在抛物线上是否还存在点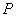 (点 (点 除外),使△ 除外),使△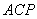 仍然是以 仍然是以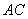 为直角边的等腰直角三角形?若存在,求所有点 为直角边的等腰直角三角形?若存在,求所有点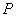 的坐标;若不存在,请说明理由。 的坐标;若不存在,请说明理由。
解析:⑴如图10,过点 作 作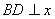 轴,垂足为 轴,垂足为 。易证△ 。易证△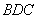 ≌△ ≌△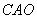 ,得 ,得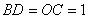 , ,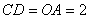 ,即点 ,即点 的坐标为(3,1) 的坐标为(3,1)
⑵将点 的坐标代入 的坐标代入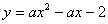 中,求得 中,求得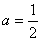 ,即所求抛物线的解析式为: ,即所求抛物线的解析式为: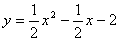 。 。
⑶假设存在点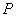 ,使△ ,使△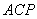 是直角三角形。即 是直角三角形。即
①如图10,若以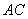 为直角边,点 为直角边,点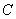 为直角顶点,则延长 为直角顶点,则延长 至点 至点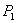 使得 使得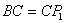 ,得到等腰直角三角形 ,得到等腰直角三角形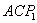 ,过 ,过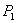 作 作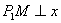 轴,垂足为 轴,垂足为 。易证△ 。易证△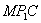 ≌△ ≌△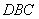 ,即 ,即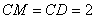 , , ,易知点 ,易知点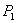 的坐标为( 的坐标为( , , ),经检验 ),经检验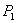 在抛物线 在抛物线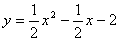 上。 上。
②如图11,若以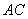 为直角边,点 为直角边,点 为直角顶点,则过点 为直角顶点,则过点 作 作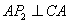 ,使得 ,使得 ,得到等腰直角三角形 ,得到等腰直角三角形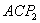 ,过点 ,过点 作 作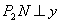 轴,垂足为 轴,垂足为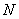 ,同样可证△ ,同样可证△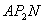 ≌△ ≌△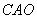 。可得点 。可得点 的坐标为( 的坐标为( ,1),经检验 ,1),经检验 同样在抛物线 同样在抛物线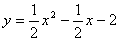 上。 上。
③如图12,若以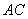 为直角边,点 为直角边,点 为直角顶点,则过点 为直角顶点,则过点 作 作 ,使得 ,使得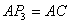 ,得到等腰直角三角形 ,得到等腰直角三角形 ,过点 ,过点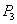 作 作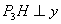 轴,垂足为 轴,垂足为 ,同样可证△ ,同样可证△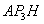 ≌△ ≌△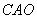 。可得点 。可得点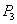 的坐标为(2,3),经检验 的坐标为(2,3),经检验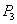 不在抛物线 不在抛物线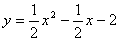 上。 上。
评析:例3实际上是由2010北京市密云县的一道中考试题改编而成。
中考链接:(2010密云)如图13,将腰长为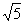 的等腰 的等腰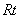 △ △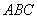 ( ( 是直角)放在平面直角坐标系中的第二象限,其中点 是直角)放在平面直角坐标系中的第二象限,其中点 在 在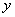 轴上,点 轴上,点 在抛物线 在抛物线 上,点 上,点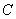 的坐标为(-1,0). 的坐标为(-1,0).
⑴点 的坐标为 ,点 的坐标为 ,点 的坐标为 ; 的坐标为 ;
⑵抛物线的关系式为 ,其顶点坐标为 ;
⑶将三角板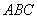 绕顶点 绕顶点 逆时针方向旋转90°,到达△ 逆时针方向旋转90°,到达△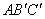 的位置.请判断点 的位置.请判断点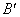 、 、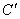 是否在(2)中的抛物线上,并说明理由。 是否在(2)中的抛物线上,并说明理由。
例4:(绍兴)抛物线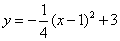 与 与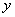 轴交于点 轴交于点 ,顶点为 ,顶点为 ,对称轴 ,对称轴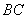 与 与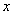 轴交于点 轴交于点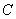 . .
⑴如图14,求点 的坐标及线段 的坐标及线段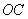 的长; 的长;
⑵点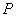 在抛物线上,直线 在抛物线上,直线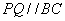 交 交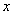 轴于点 轴于点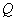 ,连接 ,连接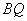 .①若含 .①若含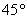 角的直线三角板如图15所示放置,其中,一个顶点与 角的直线三角板如图15所示放置,其中,一个顶点与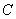 重合,直角顶点 重合,直角顶点 在 在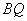 上,另一顶点 上,另一顶点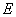 在 在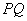 上,求直线 上,求直线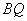 的函数解析式; 的函数解析式;
②若含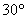 角的直角三角板一个顶点与点 角的直角三角板一个顶点与点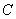 重合,直角顶点 重合,直角顶点 在直线 在直线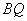 上,另一个顶点 上,另一个顶点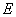 在 在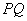 上,求点 上,求点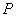 的坐标.。 的坐标.。

解析:⑴把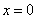 代入抛物线解析式得 代入抛物线解析式得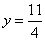 ,即 ,即 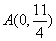 , ,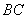 为对称轴, 为对称轴, ,∴ ,∴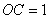 。 。
(2)①如图15,过点 分别作 分别作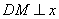 轴, 轴,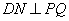 ,垂足分别为 ,垂足分别为 , ,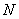 。 。
先证四边形 为矩形,再证△ 为矩形,再证△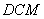 ≌△ ≌△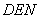 ,可得四边形 ,可得四边形 为正方形。即 为正方形。即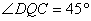 ,∴△ ,∴△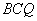 为等腰直角三角形, 为等腰直角三角形,
∴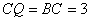 ,∴ ,∴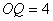 ,即 ,即 、 、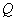 的坐标为 的坐标为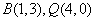 ,设直线 ,设直线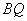 的函数解析式为 的函数解析式为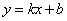 ,求得 ,求得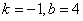 ,所求直线 ,所求直线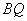 的函数解析式为 的函数解析式为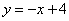 。 。
②当点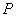 在对称轴的右侧时,如图16,过点 在对称轴的右侧时,如图16,过点 作 作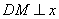 轴,垂足为点 轴,垂足为点 ,过点 ,过点 作 作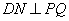 ,垂足为 ,垂足为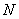 ,设点 ,设点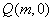 , ,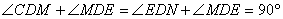 , ,
∴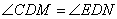 ,∴ ,∴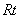 △ △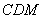 ∽ ∽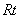 △ △ ,∴ ,∴ , ,
∵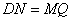 ,∴ ,∴ ,∴ ,∴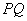 ∥ ∥ ,∴ ,∴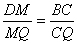 ,∴ ,∴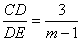
赏析:以上试题,借助三角板和函数基本图形的基本特征出发,体现了以下特点:
1.试题背景突出学科核心主干.把握数学问题的本质
核心主干是数学知识的结构中的“连结点”,在上面的试题中,题目以函数图象为载体,将三角板在函数图象中的不同放置方式作为试题的基本背景,如例1将含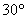 的直角三角板放在直角坐标系中与反比例函数图象相结合设置了一个操作性的对称变换的综合性试题。例4分别将含 的直角三角板放在直角坐标系中与反比例函数图象相结合设置了一个操作性的对称变换的综合性试题。例4分别将含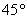 、 、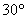 角的直线三角板按题中要求放置,考查了一次函数、二次函数、三角形全等和相似等初中数学的核心内容。试题的巧妙之处在于问题中的三角板为求解问题提供的数量依据。把握数学问题的本质,体现数形结合。 角的直线三角板按题中要求放置,考查了一次函数、二次函数、三角形全等和相似等初中数学的核心内容。试题的巧妙之处在于问题中的三角板为求解问题提供的数量依据。把握数学问题的本质,体现数形结合。
2.试题解法基于数学活动经验,关注学生的学习过程
以上试题的一个基本特点是:基于学生数学活动经验,关注“过程与方法”在获得、应用数学知识的过程中的重要作用。解决以上试题的数学活动经验主要包括2个层次:第一,来源于日常生活经验,如对的“三角板”的直接认识;第二,建立在日常生活经验基础之上的探究活动,如例2将一把含30°角的直角三角板的直角顶点置于平面直角坐标系的原点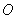 处旋转,探索在旋转过程中三角板与抛物线的交点的连线段 处旋转,探索在旋转过程中三角板与抛物线的交点的连线段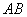 总经过一个固定的点 总经过一个固定的点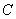 ( (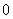 , ,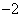 )。 )。
3.试题考查注重理性数学思维,体现能力立意命题理念
数学不仅是一种重要的“工具”和“方法”,而是人们学习的一种思维模式。在解决以上试题的过程中,学生要通过观察、实验、归纳、类比等获得猜想,并在解决问题的过程中进行合情推理,有条理地表达自己的思考过程。如例3以二次函数为载体,设置了一块等腰直角三角板放在直角坐标系第一象限,斜靠在两坐标轴上的情境,要求探索是否还存在一点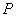 ,使△ ,使△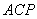 仍然是以 仍然是以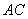 为直角边的等腰直角三角形,要用分类思考方法。强调了数学素养,以能力立意,以考查学生的思维品质为出发点和归宿,还考虑到学生升入高中学习所必备的数学知识和素质,考查了进一步学习的潜质。
(责任编辑:admin) 为直角边的等腰直角三角形,要用分类思考方法。强调了数学素养,以能力立意,以考查学生的思维品质为出发点和归宿,还考虑到学生升入高中学习所必备的数学知识和素质,考查了进一步学习的潜质。
(责任编辑:admin) |




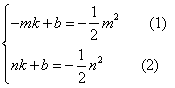 ,解得
,解得


