|
2011年数学中考试题分类赏析 贵州省道真县玉溪镇中心学校 胡 军 在本年度中考试题中，不少命题专家从应试者的心理承受能力出发，设计出了不少既考查学生对数学核心概念、思想方法的理解及运用水平，又使学生在考试过程中经历数学化的过程，从而提高自身的文化素养和创新意识的试题。 1.传承数学文化、让学生体验数学化的科学价值 新课标指出：“数学是人类的一种文化，它的内容、思想、方法和语言是现代文明的重要组成部分”。 “是人类社会进步的产物，也是推动社会发展的动力”。中考作为一种社会文化现象，必然要从属和服务于社会意识形态和特定的文化结构，必须要承载社会赋予其特定的功能——数学化。 例1：（温州）我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“赵爽弦图”（如图1—1）。图1—2由弦图变化得到，它是由八个全等的直角三角形拼接而成。记图1—2中正方形 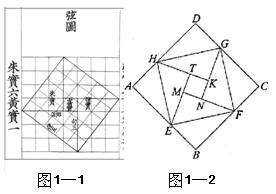 ，正方形 ，正方形 的面积分别为 ，若 =10，则 的值是 。 解析：由题意可知，  ， ， 。又由=10，易得：的值是 赏析：勾股定理是人类最伟大的十个科学发现之一。有十分悠久的历史，两千多年来，人们对勾股定理的证明颇感兴趣，因为这个定理太贴近人们的生活实际，以至于古往今来，下至平民百姓，上至帝王总统都愿意探讨和研究它。赵爽的证明可谓别具匠心，极富创新意识。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系，既具严密性，又具直观性，为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范。学生通过解此题，进一步体验了形数统一的思想方法，又一次经历了认识勾股定理的数学化过程。受到优秀文化的熏陶，传承了中华民族悠悠五千年文化史。 2. 关注问题情境、让学生经历数学化的思维过程 在命制中考试题中，如何创设试题情境是一种智慧的挑战。试题情境需要命题教师对教学本身进行周密思考与精心设计，试题情境要学生在应试过程中自己去经历、体会、理解，要有让学生思考的时间和空间，使学生在一个曾经历过的熟悉的背景下，产生一种巨大的无形的导引效应，使自己全身心投入到解决问题的数学化过程活动中，从自己的经验出发，运用属于自己的方式和策略，寻找解决问题的方法，发现和整理属于自己的不同形式的解题策略，经历数学化的过程。 例2：（南京市）： 问题情境 已知矩形的面积为  （为常数， ），当该矩形的长为多少时，它的周长最小？最小值是多少？数学模型 设该矩形的长为  ，周长为 ，则与的函数关系式为 。探索研究 ⑴我们可以借鉴以前研究函数的经验，先探索函数 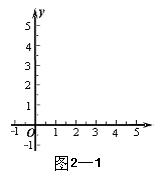 的图象性质。 ① 填写下表，在图2—1中画出函数的图象：
②观察图象，写出该函数两条不同类型的性质； ③在求二次函数  的最大（小）值时，除了通过观察图象，还可以通过配方得到．请你通过配方求函数 的最小值。解决问题 ⑵用上述方法解决“问题情境”中的问题，直接写出答案。 解析：⑴①将表中 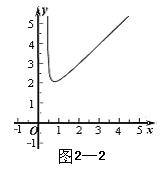的值代入中计算可得 的值分别为：  ， ， ，2，，，。描点并画出函数  的图象如图2—2所示。 ②本题答案不唯一。要根据图象，可得：当 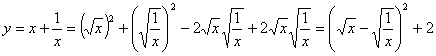 时，随增大而减小；当 时,随增大而增大；当 时函数的最小值为2等。③  当  ,即时，函数的最小值为2． ⑵当该矩形的长为  时，它的周长最小，最小值为 ．赏析：本题首先提出一个具体的问题情境，即“已知矩形的面积为 （为常数，），当该矩形的长为多少时，它的周长最小？最小值是多少？”让学生借鉴已经掌握的研究函数的经验，突出学科结合与高中内容的衔接，先探索函数的图象性质，再解决“问题情境”中提出的问题。其过程就是经历数学化的思维过程。试题注重创造“最近发展区”， 引发学生思考，让学生在思考中体验知识的形成过程，让学生始终处于“思考——收获——再思考——再收获”的这样一种情感体验之中。用睿智的语言加以点化，突现评价的导向功能，从而激发和培养学生的数学化思考，引领学生的思维往纵深发展，保证学生应试过程中在和谐融洽的气氛中按既定目标顺利进行。例3：（盐城） 情境观察： 将矩形 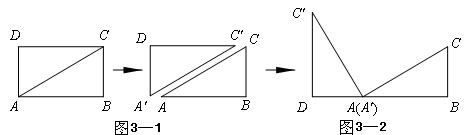纸片沿对角线 剪开，得到△ 和△ ，如图3—1所示，将△的顶点 与点 重合，并绕点按逆时针方向旋转，使点 、 、 在同一条直线上，如图3—2所示。观察图6可知：与  相等的线段是 ▲ ， ▲ °。 问题探究 如图3—3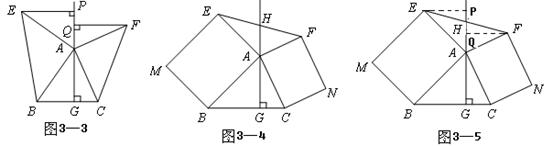，△ 中， 于点 ，以为直角顶点，分别以 、为直角边，向△外作等腰 △ 和等腰△ ，过点 、 作射线 的垂线，垂足分别为 、 .。试探究 与 之间的数量关系，并证明你的结论。 拓展延伸 如图3—4，△ 中，于点，分别以、为一边向△外作矩形 和矩形 ，射线交 于点 。若 ， ，试探究 与 之间的数量关系，并说明理。解析：情境观察：易见与 相等的线段是 ，它们是矩形的对边。 。问题探究：找一个可能与 和都相等的线段 。考虑 △ ≌△ ，这用 易证，得出 。同样考虑△ ≌△ ，得出 ，从而得证。拓展延伸：如图3—5，过点 作 ， ，垂足分别为、。与问题探究相仿，只不过将全等改为相似，证出，再证△ ≌△ ，从而得证。赏析：本题是研究性学习问题，在问题设计上层层深入，每一步都为下一步的思维活动打下基础，是一个蕴涵了让学生经历观察、猜测、合情推理、有条理论证的数学化思维过程，考查了基于数学实验的数学问题形成的一般思路及探究能力。 3.回归教育本原、贴近学生数学化发展需求 陶行知先生曾说过：“教育必须做到解放学生的眼睛，让他们亲自看一看；解放学生的大脑，让他们亲自想一想；解放学生的嘴巴，让他们亲自说一说；解放学生的双手，让他们亲自做一做。”我们认为，这是对素质教育的最佳诠释。回归教育本原、贴近学生数学化发展需求，是全面实施数学素质教育的根本所在。中考命题中如何从具体情境中抽象出数学材料，并将获得的材料符号化，体现了数学问题源于教学但高于教学的教学理念，使试题始终散发着“数学味”，促进学生个性得充分发展一直是各地命题专家关注的热点。 例4（北京）：阅读下面材料： 小伟遇到这样一个问题，如图4—1，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点O。若梯形ABCD的面积为1，试求以AC，BD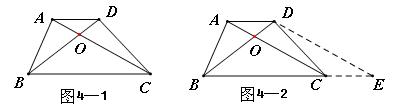，  的长度为三边长的三角形的面积。 小伟是这样思考的：要想解决这个问题，首先应想办法移动这些分散的线段，构造一个三角形，再计算其面积即可。他先后尝试了翻折，旋转，平移的方法，发现通过平移可以解决这个问题。他的方法是过点D作AC的平行线交BC的延长线于点E，得到的△BDE即是以AC，BD， 的长度为三边长的三角形（如图4—2）。参考小伟同学的思考问题的方法，解决下列问题： 如图4—3，△ABC的三条中线分别为AD，BE，CF。 ⑴在图3中利用图形变换画出并指明以AD，BE，CF的长度为三边长的一个三角形（保留画图痕迹）； ⑵若△ABC的面积为1，则以AD，BE，CF的长度为三边长的三角形的面积等于_______。  解析：⑴本题画法很多，答案不唯一。如： 方法一：如图4—4，过 作的平行线与过 作的平行线相交于点，则△ 为所求。方法二：如图4—5，延长 至，使 ，取 的中点。△ 为所求；⑵如图4—5，由已知易得  ，要求△的面积，需要证△的面积等于四边形 面积。由⑴知四边形 是平行四边形，设 与 交于 ，与交于 ，则 ，有 ， （同底 且等高）。两式相加可得结果。本题图形的本质特征是：以三角形三条中线为边的三角形面积是原三角形面积的 。例5： (绍兴)数学课上，李老师出示了如下题目。 在等边三角形 中，点在上，点在 的延长线上，且 ，如图5—1，试确定线段 与 的大小关系，并说明理由。小敏与同桌小聪讨论后，进行了如下解答： ⑴特殊情况，探索结论 当点 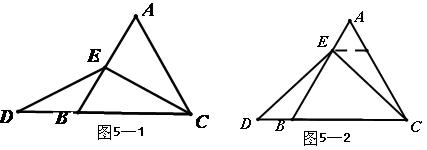为的中点时，如图5—1，确定线段与 的大小关系，请你直接写出结论： （填“>”,“<”或“=”）。 ⑵特例启发，解答题目 解：题目中， 与的大小关系是： （填“>”,“<”或“=”）.理由如下：如图5—2，过点作 ，交 于点。（请你完成以下解答过程）⑶拓展结论，设计新题 在等边三角形  中，点在直线上，点在直线 上，且 .若 的边长为1， ，求 的长（请你直接写出结果）。解析：解析：⑴由题意易知：  ⑵由⑴的结论猜想 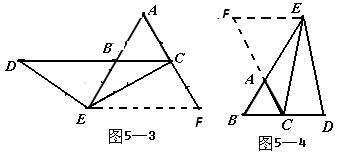。然后证明此结论。如图5—2，过点 作，交于点。易知△ 是等边三角形，即 ， 。由 ， ，得 ，又已知 ，所以△ ≌△ 。所以 ，即。 ⑶此时实际上是图形的变式，变式图5—3时结果是1，变式图5—4为时结果是3。 赏析：此上两题都以范例的形式给出，并在解决问题的过程中暗示解题思路，要求学生在理解的基础上进行迁移运用，再以活动中获得的数学经验与知识解决新问题。其实际是在中考中让学生回归教育的本原，求探索基本图形本质特征，贴近学生数学化发展需。体现了数学问题源于教学但高于教学的教学理念，使试题始终散发着“数学味”。 4.立足核心内容、寻求试题考查功能数学化 立足学科核心内容，寻求试题的综合性考查功能数化是近年来各地中考试题的一大特色。 例6（遵义）：已知抛物线 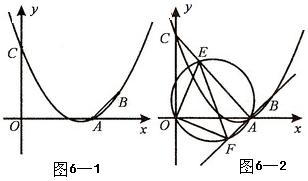 经过 ,  两点，且与轴交于点。⑴求抛物线 的函数关系式及点的坐标；⑵如图6—1,连接 ，在题⑴中的抛物线上是否存在点，使△ 是以为直角边的直角三角形？若存在，求出点的坐标；若不存在，请说明理由； ⑶如图6—2,连接 ，为线段上任意一点（不与、重合）经过、、 三点的圆交直线于点，当△ 的面积取得最小值时，求点的坐标。解析：第⑴小题，利用待定系法将 、两点的坐标代入中得到一个二元一次方程组，求出、 的值，再求点的坐标；第⑵小题，如图6—3，假设存在，分两种情况： ①连接 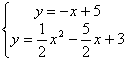, ,易得点 与点重合，即点的坐标为（0，3）；②当  时,过作 ∥,交抛物线于点 ，由(3,0), (0,3)，可得直线的函数关系式为 ，将直线从向平移（实际上是2个单位）与直线重合.则直线的函数关系式为 由  ,求得 或 ，因 点的坐标为（4，1），所以(4,1) 舍去，即的坐标为 (-1,6)。 第⑶小题，如图6—2，首先观察并判断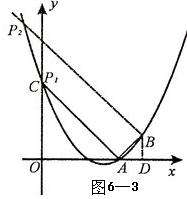△  为等腰直角三角形，由点在线段上,设 ， ，∴  = = ∴当  时,  取最小值,此时 ，∴ 。 赏析：题目以抛物线为载体，设置了由点的运动变化对三角形、圆的变化产生的影响的综合背景，解决与抛物线有关的点的坐标及三角形的面积最值问题。如在“该抛物线上是否存在点 ，使△是以为直角边的直角三角形”和“为线段上任意一点（不与、重合）经过、、三点的圆交直线于点，……”。这样的变化使题目的各种关系变得复杂，学生要用动态的观点来分析图形中的相互关系。在知识点上主要考查了二元一次方程组、一元二次方程、一次函数、二次函数、直角三角形、三角形的面积、勾股定理、圆等初中数学的核心内容；在能力上考查学生在动态背景下处理几何关系的认识能力与函数知识的应用能力；在思想方法上考查了待定系数法、配方法、方程思想、函数思想、数形结合思想及分类讨论的思想等；试题的呈现自然、简洁、和谐，提升了学生对数学本质的思考。由试题的多种解法为学生提供解题过程的开放空间，体现了试题考查功能数学化。
(责任编辑：admin) |
