|
小小三角板 数学大舞台 山东省汶上县第二实验中学 李启锋 三角板是教师、学生很熟悉的学习用具了,在近年来的数学中考题中以它为载体出现的试题层出不穷,屡见不鲜,从选择题、填空题到中等题,再到压轴题,均有涉猎,现采撷了一些考题供大家参考。 1.(2011?遵义)把一块直尺与一块三角板如图放置,若∠1=45°,则∠2的度数为( ) 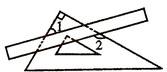 A、115° B、120° C、145° D、135° 考点:平行线的性质。 分析:由三角形的内角和等于180°,即可求得∠3的度数,又由邻补角相等,求得∠4的度数,然后由两直线平行,同位角相等,即可求得∠2的度数. 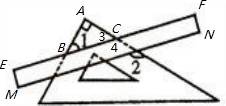 解答:解:在Rt△ABC中,∠A=90°, ∵∠1=45°, ∴∠3=90°﹣∠1=45°, ∴∠4=180°﹣∠3=135°, ∵EF∥MN, ∴∠2=∠4=135°. 故选D. 点评:此题考查了三角形的内角和定理与平行线的性质.注意两直线平行,同位角相等与数形结合思想的应用. 2.(2011湖南省娄底市)如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( ) 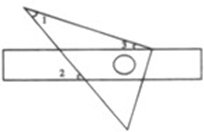 A、80 B、50 C、30 D、20 考点:平行线的性质;三角形的外角性质。 专题:计算题。 分析:由BC∥DE得内错角∠CBD=∠2,由三角形外角定理可知∠CBD=∠1+∠3,由此可求∠3. 解答:解:如图,∵BC∥DE,∴∠CBD=∠2=50°, 又∵∠CBD为△ABC的外角, ∴∠CBD=∠1+∠3, 即∠3=50°﹣30°=20°. 故选D. 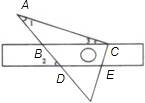 点评:本题考查了平行线的性质,三角形的外角性质,关键是利用平行线的性质,将所求角与已知角转化到三角形中,寻找角的等量关系. 3.(2011年河南省)将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,则∠1的度数为______________.  考点:平行线的性质;三角形的外角性质。 专题:计算题。 分析:由AB∥DE得∠ABE=∠E, 由三角形外角定理可知∠1=∠ABE+∠A,由此可求∠1. 解答:∵AB∥DE,∴∠ABE=∠E=30°, 又∵∠1为△ABC的外角, ∴∠1=∠ABE+∠A, 即∠1=30°+45°=75°. 点评:本题重点考察平行线的性质、三角形的外角,关键是将所求角与已知角转化到三角形中。 4. (2011年龙岩市)一副直角三角板叠放如图所示,现将含45°角的三角板ADE固定不动,把含30°角的三角板ABC绕顶点A顺时针旋转∠α(α=∠BAD且0°<α<180°),使两块三角板至少有一组边平行。 (1)如图①,α=______°时,BC∥DE; (2)请你分别在图②、图③的指定框内,各画一种符合要求的图形,标出α,并完成各项填空: 图②中α=______°时,______∥______;图③中α=______°时,______∥______。   考点:平行线的知识,旋转的性质。 专题:计算题 分析:(1)由旋转的性质得∠α=∠DAE-∠BAC=150 (2)如下图②∠α=∠B=600时,BC∥DA; 如下图③∠B=∠BAE,即∠α=∠BAE+∠DAE=600+450=1050 时,BC∥EA(或∠D+∠DAC=1800,即∠α=1800 -∠D -∠BAC=1050 时,DE∥AC;或∠D+∠α=1800,即∠α=1800-∠D=1350时,DE∥AB)。 点评:本题考察平行线的知识,旋转的性质。关键是找准在旋转的过程中哪个边和哪个边平行,考察学生的空间想象能力。  5.(2011年株洲市压轴题)孔明是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线 (1)若测得 (2)对同一条抛物线,孔明将三角板绕点 (3)对该抛物线,孔明将三角板绕点   考点:坐标系的知识、二次函数的知识,对称的性质,三角形的相似,方程的知识等等。 专题:压轴题。 解答: (1)设线段 ∴ 将 (2)解法一:过点 ∴ ∴△  ∴ ∴设点 ∴ 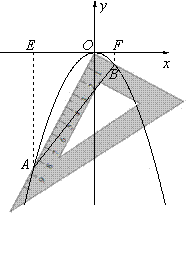  解法二:过点 ∴  ∴ 设点 ∴ 解法三:过点 设 ∴ 解得: (3)解法一:设 设直线 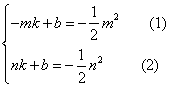 , ,∴ 又易知△ ∴ 解法二:设 直线 化简,得 又易知△ ∴ 点评:这是一道以三角板为载体的综合题,解决本题我们默认了一个事实是三角板中的∠AOB=900。 一副三角板,实际上是两个特殊三角形,以它为媒介来出的中考试题中,我们要认清这样的一些事实:它的每个角是多少度,边与边之间的数量关系,角与边之间的关系,也就是解直角三角形的知识。充分利用这些隐含的条件,再结合其他的数学知识来解决问题。 下面再给出一些练习题:   1. (黄石市2011年)将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图(1),则三角板的最大边的长为( ) A.  2、(2011年四川绵阳)将一副常规三角尺按如图方式放置,则图中∠AOB的度数为 A、75° B、95° C、105° D、120° 3. (2011年恩施自治州) 将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是: A、43° B、47° C、30° D、60° 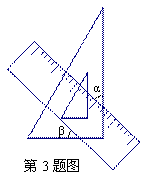  4、(2011?金华)如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )  A、30° B、25° C、20° D、15° 5.(2011年山东省东营市)一副三角板,如图所示叠放在一起.则图中∠α的度数是( ) A.75° B.60° C.65° D.55° 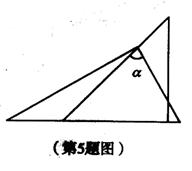 6、(2011?宜昌)如图是教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=   A、30 C、10 7、(2011四川乐山)如图,直角三角板ABC的斜边AB=12㎝,∠A=30°,将三角板ABC绕C顺时针旋转90°至三角板 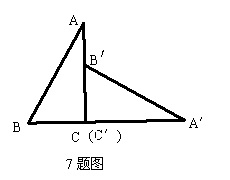  (A) 6㎝ (B) 4㎝ (C) (6- (D)( 8.(2011年山东省菏泽市)一次数学活动课上,小聪将一副三角板按图中方式叠放, 则∠ A.30° B.45° C.60° D.75°   9. (2011年江西省中考题)一块直角三角板放在两平行直线上,如图所示,∠1+∠2=___________度.   10 (2011年江西省南昌市)如图所示,两块完全相同的含30°角的直角三角板叠放在一起,∠DAB =30°,有以下四个结论:①AF⊥BC ②△ADG≌△ACF ③O为BC的中点 ④AG︰DE= 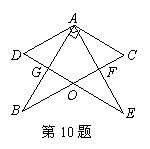  11.(2011年山东省枣庄市)将一副三角尺如图所示叠放在一起,若   12.(2011年内蒙古包头市)在Rt△ABC中,AB=BC=5,∠ABC=90?.一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB、BC或其延长线于点E、F,图①、②是旋转三角板所得图形的两种情况. (1)三角板绕点O旋转,△COF能否成为等腰直角三角形?若能,指出所有情况(即给出△COF是等腰直角三角形时BF的长);若不能,请说明理由. (2)三角板绕点O旋转,线段OE和OF之间有什么数量关系?用图①或图②加以证明. (3)若将三角板的直角顶点放在斜边上的点P处(如图③),当AP∶AC=1∶4时,PE和PF有怎样的数量关系?证明你发现的结论. 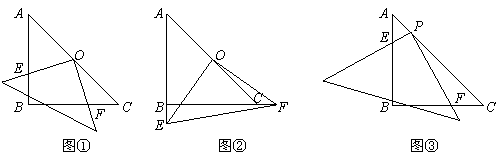  13.(2011年山东省威海市)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长。 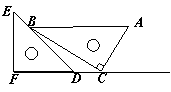  练习题参考答案:1 D; 2 C; 3 B;4 B;5 75°;6 C;7 (C);8 75°; 9 90° ; 10 ①②③④ ;11 24.5; 12 提示:(1)BF= (3)PE∶PF=1∶3 过点P分别作AB BC的垂线,利用相似三角形证明。 13 提示:CD=15-5 |
