|
说理型试题 因为说理型试题考查的知识点较多，它不仅考查学生的基础知识，而且考查学生的创新能力，数形结合能力，分类讨论能力，探索问题能力，所以成为近几年中考试题的命题热点。 例1、（2005年台州）如图，在平面直角坐标系内，⊙C与y轴相切于D点，与x轴相交于A（2，0）、B（8，0）两点，圆心C在第四象限。 （1）求点C的坐标； （2）连结BC并延长交⊙C于另一点E，若线段BE上有一点P，使得  ，能否推出AP⊥BE？请给出你的结论，并说明理由；（3）在直线BE上是否存在点Q，使得 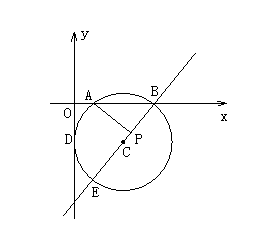 ？若存在，求出点Q的坐标，若不存在，也请说明理由。 解：  说明：考查了相似形的判定及性质应用，切割线定理、勾股定理、三角函数等有关知识，本题关键是还体现了分类思想. 练习一 1、（2005年贵阳市）在Rt⊿ABC中，∠C =  ，AC = 6，BC = 8，点O在CB上，且AO平分∠BAC，CO = 3（如图所示），以点O为圆心， 为半径画圆；（1） 取何值时，⊙O与AB相切；（2） 取何值时，⊙O与AB有两个公共点？（3）当⊙O与AB相切时，设切点为D，在BC上是否存在点P，使⊿APD的面积为⊿ABC的面积的一半？若存在，求出CP的长，若不存在，请说明理由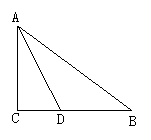；  2、（2005年武汉）如图，在平面直角坐标系中，点  的坐标为（－4，0），以点为圆心，8为半径的圆与x轴交于A、B两点，过点A作直线l与x轴负方向相交成60°角。以点 （13，5）为圆心的圆与x轴相切于点D. （1）求直线l的解析式； （2）将⊙ 以每秒1个单位的速度沿x轴向左平移，同时直线l沿x轴向右平移，当⊙第一次与⊙相切时，直线l也恰好与⊙第一次相切，求直线l平移的速度；（3）将⊙ 沿x轴向右平移，在平移的过程中与x轴相切于点E，EG为⊙的直径，过点A作⊙的切线，切⊙于另一点F，连结A、FG，那么FG·A的值是否会发生变化？如果不变，说明理由并求其值；如果变化，求其变化范围。 (责任编辑：admin) |