|
一道中考题的解法探究及思考 湖北省安陆市洑水初中 王官清 一道以正方形为背景的中考题，很多同学解答时，往往找不到解题的突破口，不能综合运用所学数学知识，思维缺乏灵活性、连贯性。下面的六种解法给同学们提供借鉴。 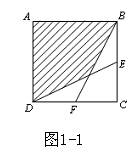 题 （2009贺州）如图1-1，正方形ABCD的边长为1cm，E、F分别是BC、CD的中点，连接BF、DE，则图中阴影部分的面积是 cm2． 分析：图中阴影部分是不规则四边形，须作辅助线转化为规则四边形或三角形，才能运用规则四边形或三角形的面积公式求解。也可考虑间接求解：先求出空白部分的面积，再用正方形的面积减去空白部分面积。题目中重要的是要考虑中点的如何运用。 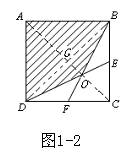 解法一：如图1-2，连接AC、BD交于G,根据正方形性质，G是BD中点，显然，O是△BDC的重心。CG经过O点。∴OG=  CG，∴△ BOG的面积等于△BCD的面积的，即 ，∴阴影部分的面积= .点评：正方形常见的辅助线是正方形的对角线。由正方形对角线的性质迅速得到O是三角形BCD的重心，利用三角形重心的性质使解答比较简捷。（重心性质见人教版八年级下册数学教材第115页第15题的结论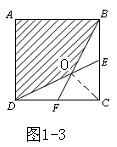）。  解法二：如图1-3，连接OC， ∵F分别是CD的中点，∴△DOF的面积和△COF面积相等. 由FC=EC，BC=DC，得  ， .由 ， , 得 ,  .由OC=OC,CF=CE,OF=OE, 得△COF≌△COE， ∴△DOF的面积等于△DCE的面积的 ，即△DOF的面积=× ×1×= ∴空白部分的面积等于△DOF的面积的4倍，即为4× =，∴阴影部分的面积=1－ = .点评：解答过程反复运用了全等三角形的有关知识，充分发挥了全等三角形在处理几何问题时的工具性。 解法三：如图1-2，同解法一可知，AC过O点。而AC是正方形ABCD的对称轴， ∴  ,,△COF≌△COE，∵AB∥FC,∴△ABO∽△CFO,相似比为AB:FC=2,面积比为4，设△CFO的面积为a，则△ABO的面积为  .同理△ADO的面积为,△CEO的面积为 ,∵E、F分别是BC、CD的中点，∴  , ，∴  ,∴阴影部分的面积= .点评：正方形的对称性、相似三角形性质的灵活运用，使解答比较巧妙。解答中根据所设，应用相似三角形的性质得到了图中有关三角形的面积关系，值得关注。 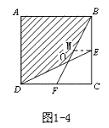 解法四：如图1-4，作EM∥DC交BF于M. ∴  相似比为，面积比为 ，设 ，则 ， （由证法二知）， ， 。∵  ,相似比为，面积比为，∴ ，且  .∴图中空白部分面积为  ，∴阴影部分的面积=1-=.点评：全等三角形和相似三角形性质综合应用，思路更加开阔灵活。 解法五：如图1-5，过O作GH∥DC,PQ∥DC,分别交正方形四边于G、H、P、Q, 设HO= 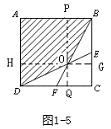 ，则OG= . （由证法二知），∴DO=BO.又 ，∴Rt△DOQ≌Rt△BOG,∴DQ=BG, ∴HO=PO,∴AHPO、CGOQ为正方形。∴阴影部分的面积等于矩形ADQP的面积。 由  得 ∴矩形ADQP的面积=1× ==阴影部分的面积。点评：把不规则四边形用割补法转化为矩形是本解法的亮点。  解法六：如图1-6，连接BD、EF, ∵ E、F分别是BC、CD的中点, ∴EF∥BD,  ,∴ ,相似比为，面积比为.设  的面积为,则 面积为4，∵BO:OF=2:1,∴  和 的面积都为 ，而  , ∴ ， ，阴影部分的面积=  .点评：把求阴影部分的面积转化为求两个三角形分的面积。充分体现了转化的数学思想。 归纳与思考：以上各种解法，使用的知识点较多，其中相似三角形、全等三角形的性质为解答提供了主要依托，使解答入口更宽。各种解法有共性，也有差别。观察思考的角度略有不同。解答中注重了转化的思想方法运用：解法一、解法六是把阴影部分面积转化为两个三角形的面积之和，解法二、解法三、解法四是把阴影部分面积转化求正方形面积与空白部分面积之差，而空白部分的面积求法由辅助线的不同而不同。解法五是把不规则的阴影部分面积转化为矩形面积来求。解答中也注重了方程的思想，后面四种解法都有“设、列、求”。而解法一应用三角形重心的性质，解答尤为简捷。 (责任编辑：admin) |