|
中考新概念四边形赏析 湖北省郧县第二中学 杨育颖 新概念问题是近年来中考试题中，涌现出的一种新型试题，它既能考查学生适应新问题、接受新知识、认识新事物的能力，又能考查学生的自学能力，信息的收集、迁移和应用能力。 该试题新颖别致，颇具魅力，已成为中考试题中的一朵奇葩，现就四边形中新概念题举两例供大家赏析。 一、中点四边形 例2、（内江市中考题）如图2，四边形ABCD中，E、F、G、H分别为各边的中点，顺次连接E、F、G、H，把四边形EFGH称为中点四边形。连接AC、BD，容易证明：中点四边形EFGH一定是平行四边形。 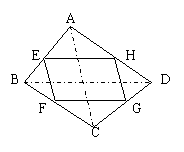 （1）如果改变原四边形ABCD的形状，那么中点四边形EFGH的形状也随之改变，通过探索可以发现：当四边形ABCD的对角线满足AC = BD时，四边形EFGH 为菱形； 当四边形ABCD的对角线满足______时，四边形EFGH为矩形； 当四边形ABCD的对角线满足______时，四边形EFGH为正方形； （2）探索三角形AEH，三角形CFG与四边形ABCD的面积之间的等量关系，请写出你发现的结论并加以证明； （3）如果四边形ABCD面积为2，那么中点四边形EFGH的面积是多少？ 分析：相对来讲，中点四边形是我们比较熟悉的一个概念。本题中，①当对角线相等时，中点四边形为菱形；②当对角线垂直时，中点四边形为矩形；③当对角线既相等又垂直时，中点四边形为正方形。探索三角形与四边形之间的面积关系，可利用相似三角形的面积比等于相似比的平方这一定理。 解：（1）AC⊥BD，AC⊥BD且AC＝BD。 （2）S△AEH＋S△CFG＝  S四边形ABCD。 证明：在△ABD中，EH= BD，所以△AEH～△ABD，所以即  ，同理可证： ，所以 。（３）由（２）的结论可知：  。二、等对角线四边形 例2、（北京市中考题） 我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形。请解答下列问题： （1）写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称； （2）探究：当等对角线四边形中两条对角线所夹锐角为60O时，这对60O角所对的两边之和与其中一条对角线的大小关系，并证明你的结论。 分析：本题以定义的形式，提出了新的数学概念“等对角线四边形”这一新知识点，要理解并结合图形后才能运用，形成一道考查同学们的阅读理解能力以及作图、应用、证明等能力的综合题。 解：（1）等腰梯形、矩形等； （2）结论：等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和大于或等于一条对角线的长。 已知：四边形ABCD中，对角线AC，BD交于点O，AC = BD，且∠AOD = 60°， 求证：BC + AD≥AC。 证明：过点D作DF∥AC，在DF上截取DE，使DE = AC，连接CE，BE， 故∠EDO = 60°，四边形ACED是平行四边形，所以△BDE是等边三角形，CE = AD，DE = BE = AC。 ①当BC与CE不在同一条直线上时（如图1），在△BCE中， 有BC + CE＞BE， ∴BC+AD＞AC。 ②当BC与CE在同一条直线上时（如图2）， 则BC + CE = BE， ∴BC + AD = AC。 综合①，②，得BC + AD≥AC。即等对角线四边形中两条对角线所夹锐角为60°时，这对60°角所对的两边之和大于或等于一条对角线的长。 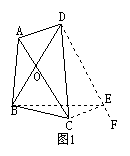 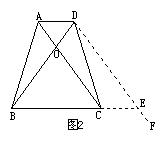 三、相似梯形 例3（台州中考题）善于学习的小敏查资料知道：对应角相等，对应边成比例的两个梯形，叫做相似梯形。他想到“平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似”，提出如下两个问题，你能帮助解决吗？ 问题一 平行于梯形底边的直线截两腰所得的小梯形和原梯形是否相似？ （1）从特殊情形入手探究。假设梯形ABCD中， AD∥BC，AB=6，BC=8，CD=4， AD=2，MN是中位线（如图2①）。根据相似梯形的定义，请你说明梯形AMND与梯形ABCD是否相似? （2）一般结论：平行于梯形底边的直线截两腰所得的梯形与原梯形______________ (填“相似”或“不相似”或“相似性无法确定”。不要求证明) 。 问题二 平行于梯形底边的直线截两腰所得的两个小梯形是否相似? （1）从特殊平行线入手探究。梯形的中位线截两腰所得的两个小梯形______________ (填“相似”或“不相似”或“相似性无法确定”。不要求证明)。 （2）从特殊梯形入手探究。同上假设，梯形ABCD中，AD∥BC，AB=6，BC=8，CD=4，AD=2，你能找到与梯形底边平行的直线PQ（点P，Q在梯形的两腰上，如图2②）， 使得梯形APQD与梯形PBCQ相似吗? 请根据相似梯形的定义说明理由。  (3)一般结论：对于任意梯形（如图2③），一定 (填“存在”或“不存在”) 平行于梯形底边的直线PQ，使截得的两个小梯形相似。 若存在，则确定这条平行线位置的条件是  = (不妨设AD= a，BC= b，AB=c，CD= d。不要求证明 ) 。 解：问题一（1）因为MN是中位线，所以MN=  ， ， ， ，显然对应边不成比例，所以梯形AMND与梯形ABCD不相似。（2）平行于梯形底边的直线截两腰所得的梯形与原梯形不相似。 问题二（1）因为MN是中位线，显然两梯形对应边不成比例，所以梯形的中位线截两腰所得的两个小梯形不相似。 （2）如果梯形APQD与梯形PBCQ相似，则  ，即 ，解得PQ=4，此时 ，又AB=6，所以AP=2，所以当AP=2，且PQ∥BC时， ，又两梯形对应角相等，所以梯形APQD与梯形PBCQ相似。（3）对于任意梯形，一定存在平行于梯形底边的直线PQ，使截得的两个小梯形相似。 此时， ，所以PQ= ，故 通过以上几例可知，解答这类问题的关键是在阅读、理解的基础上，由题中提供的信息，联系所学知识，运用联想类比、模仿迁移的方法实现信息的迁移，从而掌握符合问题的条件及其性质的运用。 (责任编辑：admin) |