提高实效 备战中考
广东省广州市白云区江高镇第三中学 王 芸
摘 要:初中毕业班的教学时间紧迫,因此在初中数学复习课教学中,要在有限的教学时间内提高复习课的教学效率。关键要:明确目标,强化学生的主体意识;优化教学方式,提高课堂实效;及时反馈,促进教学;以生为本,因材施教。以此促进学生实现知识的自主建构,提高复习课的教学效率。
关键词:初中数学;有效复习;实践
初中三年数学教学任务完成后,便进入到紧张的总复习阶段。初中复习备考是巩固知识、消化知识、运用知识、培养能力的重要手段,更重要的是从本质上提高学生的数学素养,数学应用能力,达到学以致用的目的。本文结合自己的教学实践,以《二次函数》复习学案为例,谈几点关于“如何提高数学复习课教学效率”的体会。
一、明确目标,强化学生的主体意识
心理学研究表明“人类的任何行为都有目的”。没有目标的学生在复习过程中常常表现出盲目、随意、效率低。为了强化学生的主体意识,教师应该让学生充分了解初三数学的复习要求,阶段要求和初中毕业生学业考试命题方向及试卷结构,让学生心中有数,积极参与,变被动地接受学习为主动积极地参与学习,真正成为学习的主人。例如,在课前为学生分析本章内容在中考中的地位,明确学生的复习目标:《二次函数》在广州中考题所占分值较多。题型有填空题、选择题、解答题。主要考查内容有:函数的取值范围,待定系数法,求函数图像与坐标轴的交点,简单函数图像的画法,求二次函数的顶点坐标及最大值与最小值,几何图形与二次函数的关系。难题主要放在几何图形与函数的综合探索。
二、优化教学方式,提高课堂实效
教学方式具要多层次的内涵,广义的教学方式是指实现教学目的所采取的一切手段、技术、途经,所阐述的教学方式运用的有效性不求面面俱到,仅选择其中具有代表性的几个方面加以详述。
(一)练在讲之前,调动学生积极参与
讲与练关系的实质就是知与行、理论与实践的关系。光讲不练,课堂上听懂的东西不能巩固,更不能深化;但讲得太多,不重点突出,抓不住要害,也会引起“消化不良”。先练后讲是为了让学生听课更有效率和针对性,让学生带着问题听课,使其在思想上、行动上、内容上先进入学习状态。
例如,复习第一环节设置基础复习题:
二次函数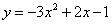 ,二次项系数是 ,一次项系数是 ,常数项是 。把二次函数 ,二次项系数是 ,一次项系数是 ,常数项是 。把二次函数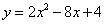 配方成 配方成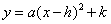 的形式为 ,它的图像是 ,开口向 ,顶点坐标是 ,对称轴是 。当 的形式为 ,它的图像是 ,开口向 ,顶点坐标是 ,对称轴是 。当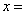 时, 时, 。此抛物线与x轴有 个交点。它的图像是由函数 。此抛物线与x轴有 个交点。它的图像是由函数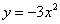 图像向 平移 个单位,再向 平移 个单位得到的。 图像向 平移 个单位,再向 平移 个单位得到的。
在此部分,可把基础概念、定理等习题化,函数图象的性质与变换规律都得到体现,以免花费大量时间整理知识结构表。
(二)精讲典型例题,善于举一反三
复习课例题的选择,应是最有代表性和最能说明问题的典型习题。应能突出重点,反映学业标准最主要、最基本的内容和要求。对例题进行分析和解答时,要注意例题之间的内在联系,可用一题多变,一题多解,一图多用来进行讲解,这样串起来的题目比较多。纵向、横向联系的知识点比较多,学生掌握的知识也就比较系统、全面。实现复习知识从量到质的转变。本节例题设置有:例1.已知二次函数的图像如图(1)所示,求其解析式。
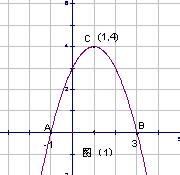
分析:(方法一)已知A、B、C三点坐标,可以设二次函数为一般形式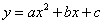 求得函数解析式 求得函数解析式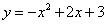 ;(方法二)已知点A、B是抛物线与x轴的交点,可以设二次函数为交点式 ;(方法二)已知点A、B是抛物线与x轴的交点,可以设二次函数为交点式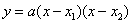 求得函数解析式 求得函数解析式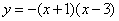 ;(方法三)已知点A、B是抛物线与x轴的交点,可求得抛物线对称轴是直线 ;(方法三)已知点A、B是抛物线与x轴的交点,可求得抛物线对称轴是直线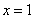 ,因此点C(1,4)是抛物线的顶点,可以设二次函数为顶点式 ,因此点C(1,4)是抛物线的顶点,可以设二次函数为顶点式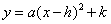 求得函数解析式 求得函数解析式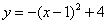 。 。
变式1.如图(2),直线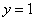 与抛物线相交于点E、F,求线段EF的长。 与抛物线相交于点E、F,求线段EF的长。
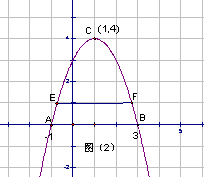
分析:由例1可知当y=1时求得点E、F坐标分别为E(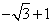 ,1),F( ,1),F(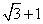 ,1),所以 ,1),所以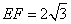 。 。
把坐标轴隐藏得到图(3)。
变式2.(参考课本第25页探究)如图(3)是抛物线形拱桥,当水面在AB时,拱顶离水面4米,水面宽4米,水面上升1米到EF时,水面宽度减少多少?(结果精确到0.01米)
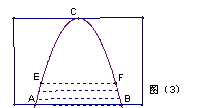 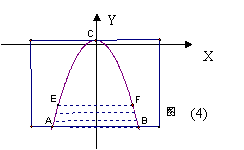 
分析:由变式1得到答案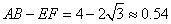 (米)。但是为了运算更简便,通常建立直角坐标系如图(4)所示,得到函数关系式 (米)。但是为了运算更简便,通常建立直角坐标系如图(4)所示,得到函数关系式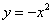 。得到答案为水面宽度减少约0.54米。 。得到答案为水面宽度减少约0.54米。
(三)用好课本,用活课本
教育实践表明:大量的机械重复强求划一的练习作业超过了学生的生理、心理负荷,使学生产生厌学、应付等逆反心理。因此,对练习作业老师要精心选编合理布置,不能过度搞题海战术。备课时可设计三种水平的习题:基础题、熟练题、发展题。使中、下学生完成基础题、熟练题──达标练习,训练他们的技能技巧;中上生、优生完成熟练题、发展题──训练他们灵活运用知识解决问题的能力,培养和发展创造思维能力。
在复习的开始阶段,首先应该重视课本知识的复习。因为课本是数学知识的载体,中考的试题也是在课本知识的基础上引申而来的。以课本为依据,用好课本,用活课本,切忌简单重复,更不能走马观花。例如(课本第22页问题):用总长为60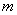 的篱笆围成矩形场地。(1)要使这个矩形面积为200 的篱笆围成矩形场地。(1)要使这个矩形面积为200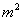 ,矩形的长和宽各是多少?(2)这个矩形面积可能为300 ,矩形的长和宽各是多少?(2)这个矩形面积可能为300 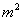 吗?若能,求出矩形的长和宽;若不能,请说明理由。 吗?若能,求出矩形的长和宽;若不能,请说明理由。
点评:对于第(2)小题,观察学生的答案,几乎都是运用一元二次方程根的情况进行判断,教师应该引导学生用函数的观点分析问题。若设矩形一边长为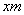 ,面积为 ,面积为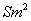 ,可得关系式 ,可得关系式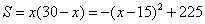 ,当 ,当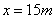 时,矩形面积最大,为 时,矩形面积最大,为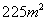 。因为300>225,所以矩形面积不可能为300 。因为300>225,所以矩形面积不可能为300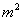 . .
教师应引导学生把知识重点、难点前后联系,重新组合,灵活而又不拘一格地驾驭教材,既充分发挥例、习题的示范性、典型性,又使解题涉及到的知识和方法得到延伸,使学生从多方面感知数学知识和方法,提高学生综合分析问题、解决问题的能力。挖掘课本例、习题的功能,可以从以下几方面入手:(1)改变题目形式(如变解答题为选择题或填空题);(2)条件与结论交换或部分交换;(3)增加条件,探索新的结论;(4)改变题目条件,对结论进行推广与引申;(5)一题多解或多题一解;(6)类比编题等。做好例、习题的教学,可以使学生进一步消化教材,也使复习有本可循。既有效地培养了学生的发散思维,又使复习收到事半功倍的效果。
(四)结合考点,分析试题,树立信心
在备考中选择训练题时,历年中考试题是最佳选择。教师要将其归类,按考查知识点、载体、解题方法等方面进行研究,结合课本的习题,进行适当的变形、拓展,然后分类给学生进行限时训练。使学生围绕考点,做到举一反三,触类旁通。这样的训练不仅可以达到巩固双基的作用,又可以让学生有挑战的动力,树立学生的自信心。
例如,选编各地中考题进行模拟训练:
1.(2010哈尔滨)在抛物线y=x2-4上的一个点是( ).
(A)(4,4) (B)(1,一4) (C)(2,0) (D)(0,4)
2.(2010年兰州)二次函数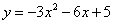 的图像的顶点坐标是( ) 的图像的顶点坐标是( )
A.(-1,8) B.(1,8) C.(-1,2) D.(1,-4)
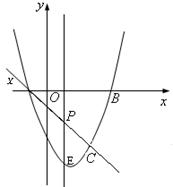
3.(2007浙江省)如图,抛物线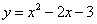 与x轴交A、B两点(A点在B点左侧),直线 与x轴交A、B两点(A点在B点左侧),直线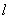 与抛物线交于A、C两点,其中C点的横坐标为2。 与抛物线交于A、C两点,其中C点的横坐标为2。
(1)求A、B 两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由。
(五)在解题教学中加强数学思想方法的训练。
数学的观念、思想和方法是数学科学的重要组成因素,是数学科学的“灵魂”,在促进学生的发展中具有决定性的作用:它是学生获得数学知识的主观手段。学生一旦把数学思想方法内化为自己的思维和行为方式,就能获得智能发展。能否运用数学思想方法进行分析问题、解决问题关系到中考的成败。纵观多年的中考题,在注重考查数学核心内容与基本能力的同时,考题中都突出了数学思想方法的理解和简单运用。因此,在复习过程中不能只在乎做了多少练习题,更重要的是对所学知识进行梳理,对推理论证及处理问题的思想方法进行总结,提高学生的主动性及分析问题解决问题的能力。
例如,为渗透数形结合思想,设置训练题:
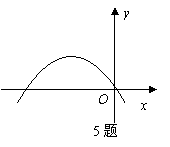
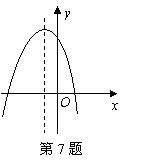
1.如图所示的抛物线是二次函数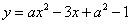 的图象,那么 的图象,那么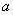 的值是 . 的值是 .
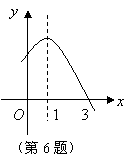
2.已知二次函数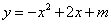 的部分图象如图所示,则关于 的部分图象如图所示,则关于 的一元二次方程 的一元二次方程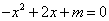 的解为 . 的解为 .
3.已知二次函数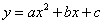 的图象如图所示,则点 的图象如图所示,则点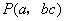 在第 象限. 在第 象限.
通过训练引导学生在分析中领悟解决问题的思想方法,使学生明确了解数学思想方法在解题中的指导作用,帮助学生真正掌握数学思想方法。
三、及时反馈,促进教学
高效的复习课,应在学生发现自身不明白问题和改正错误上下功夫,在不懂的知识和纠错方面做好笔记,充分利用学生已有的知识结构去同化新的知识,建立新的知识结构,从而做到“温故而知新”。 教师能否及时把握学生对知识的掌握和运用最好的方法是统一测试。因此,在复习过程中教师要精心选题,注重稳定典型考题、热点考题、新教材为背景的创新题的合理搭配,自编模拟题或从若干中考模拟题中精选、组合成测试题。把检测卷中易错问题,列为讲评难点查漏补缺,使学生加深理解,具备举一反三的能力。
四、以生为本,因材施教
三千年前,孔子在施教过程中,就非常注重对其众弟子日常言行的细致观察,力求全面、准确地掌握每个学生的道德、品行,然后针对具体“材质”不同的性格爱好、不同智力背景、不同的德行操守等确立不同的教育切入点,进而达到殊途同归的教育目的。班级授课面向的是全体学生,步调统一,难以兼顾到全体,两极分化情况必定日益严重。课后辅导中下生是其中一种可行的办法。但是这样将要花费老师和学生大量的时间与精力,而且收效甚微!因此,面对有差异的学生,实施有差异的教育将更有利于学生的健康心理和人格的培养。我们可以通过对学生分层、对教学内容分层,对不同层次的学生以不同的标准进行评价,使不同层次的学生经过努力都能取得较好的成绩,享受到成功的喜悦,从而激发他们学好数学的兴趣。
(一)“点”的辅导
个别辅导,不仅在课堂上,课后也特别注意对学生的辅导训练。所以选题是关键,搜集和编制了双基训练题,中等解难题,适当布置一些附加题(变试题、加深题),针对班级情况确定部分学生进行个别辅导,主要是课堂关注,练习的面批、订正等。当然这些人员、人数、时间可以根据掌握情况而适当调整、变化。
(二)“线”的辅导
小组辅导,主要是中等生,按照他们自身特点进行分组,例如女生对几何图形的识别有障碍,男生的学习习惯不好,散漫、怕烦不愿意计算、不肯主动做练习。分组后来个组与组的比赛,以此调动这些学生的积极性。
(三)“面”的辅导
班级整体辅导,采用先练习后批再评讲的方法,教师做好试卷分析工作,针对题型进行分散,举一反三解题,通性通法,各类题型的多种解法,从学生的认识情况出发,重点讲解学生易接受易想到的方法。
所谓“一勤天下无难事”,纵观数学教学的每一环节,提升数学教学有效性的空间无处不在。只要不断实践,不断摸索,就能在教学中取得丰硕的成果,使学生能以适合自己的数学学习方法得到最佳发展。
参考文献:
①苏光洁.构建符合素质教育要求的中学课堂教学模式.教育实践与研究,2001-8:8-9
②赵岩英,刘茂祥.素质教育背景下课堂教学有效性的外延浅析.现代中小学教育,2003-4:18-21
③岑志庆.新课程标准下初中数学课堂教学有效性策略研究.数学教学与研究,2007-49:28-29
④余文森.论有效教学的三条“铁律”. 中国教育学刊,2008-11:40-46
⑤费桂彬.数学有效学.教材教法,2006-4:102
(责任编辑:admin) |