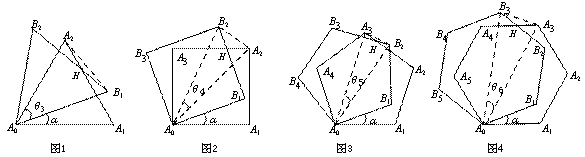
中考课题学习的酝酿与探究_中考网-中考真题答案下载-中考试题库-中考成绩查询-知识点学习方法与技巧补课解题技巧学习计划表总结-中考查分网-中考网-中考资源网-中学学科网

    中考课题学习的酝酿与探究
    江西省安福县城关中学　曹经富
    “课题学习”类试题在近年各地中考试题中频频出现,此类题型特点鲜明、内容丰富、超越常规,源于课本,又高于课本,不仅注重数学实践应用、动手探究的培养,还关注学生学习的过程和思想方法的渗透.这类试题较好地考查了学生的阅读理解能力、知识迁移能力和分析问题、解决问题的能力,这无疑为课堂教学注入了新鲜的活力。它既是一项全新的课程内容．又是一种具有现实性、问题性、实践性、综合性和探索性的新型的学习活动．经常成为呈现中考数学知识和能力的载体。现结合2011年各地中考题进行说明，希望能给大家带来一定的启示与帮助．
    一、情景问题拓展类
    例1：（2011江苏盐城）情境观察
    将矩形ABCD纸片沿对角线AC剪开，得到△ABC和△A′C′D，如图1所示.将△A′C′D的顶点A′与点A重合，并绕点A按逆时针方向旋转，使点D、A(A′)、B在同一条直线上，如图2所示．观察图2可知：与BC相等的线段是      ，∠CAC′= 　   °．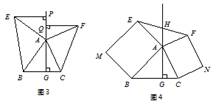

    问题探究
    如图3，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q. 试探究EP与FQ之间的数量关系，并证明你的结论.
    拓展延伸
    如图4，△ABC中，AG⊥BC于点G，分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF，射线GA交EF于点H. 若AB= k AE，AC= k AF，试探究HE与HF之间的数量关系，并说明理由.
    思路点拨：沿矩形的对角线剪开所得的两个三角形是全等的，由如图2中位置及全等关系可得BC=AD，∠CAC′=90°；在图3中，当等腰Rt△ABE和等腰Rt△ACF的直角顶点重合于直线GP上的点A时，构建了如图2所示的两个直角三角形全等的数学模型，即Rt△ABG≌Rt△EAP. Rt△ACG≌Rt△FAQ，进而得到AG=EP，AG=FQ，从而得到EP=FQ.在图4中，当背景由等腰直角三角形变为矩形时，但矩形的长与宽之比均为k,从而构建了如图2所示的两直角三角形相似（全等）的数学模型，借助相似比及 Rt△EPH≌Rt△FQH.容易得出HE=HF 。
    解：情境观察 AD（或A′D），90
    问题探究结论：EP=FQ. 证明：∵△ABE是等腰三角形，∴AB=AE，∠BAE=90°.
    ∴∠BAG+∠EAP=90°.∵AG⊥BC，∴∠BAG+∠ABG=90°，∴∠ABG=∠EAP.
    ∵EP⊥AG，∴∠AGB=∠EPA=90°，∴Rt△ABG≌Rt△EAP. ∴AG=EP.
    同理AG=FQ. ∴EP=FQ.
    拓展延伸结论： HE=HF. 理由：过点E作EP⊥GA，FQ⊥GA，垂足分别为P、Q.
    　　　　　　　　　　　　　　　

    ∵四边形ABME是矩形，∴∠BAE=90°，
    ∴∠BAG+∠EAP=90°.AG⊥BC，∴∠BAG+∠ABG=90°，
    ∴∠ABG=∠EAP.∵∠AGB=∠EPA=90°，∴△ABG∽△EAP，
    ∴ = . 同理△ACG∽△FAQ，∴ = .
    ∵AB= k AE，AC= k AF，∴ = = k，∴ = . ∴EP=FQ.
    ∵∠EHP=∠FHQ，∴Rt△EPH≌Rt△FQH. ∴HE=HF

    点评：本题以课题学习的方式呈现，解决此题的关键在于简单情景入手，准确把握相关图形的特征与模型，透过现象看到数学活动问题的本质（直角顶点重合于直线上某一点时，酝酿与构建了两直角三角形全等或相似关系），不被“动”及“变化的图形”所迷，关键是在于由特殊到一般、由简单到复杂的思维方式，这类试题不仅结论可以类比，而且思维方法、证明过程及说理过程也可通过类比得出，这种模式应引起我们的重视与关注。
    二、阅读理解类
    例5：（2011湖南永州）探究问题：
    ⑴方法感悟：
    如图①，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF，求证DE+BF=EF．
    感悟解题方法，并完成下列填空：
    将△ADE绕点A顺时针旋转90°得到△ABG，此时AB与AD重合，由旋转可得：

    AB=AD,BG=DE, ∠1=∠2，∠ABG=∠D=90°,
    ∴∠ABG+∠ABF=90°+90°=180°，
    因此，点G，B，F在同一条直线上．
    ∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．
    ∵∠1=∠2，   ∴∠1+∠3=45°．
    即∠GAF=∠_________．又AG=AE，AF=AF
    ∴△GAF≌_______．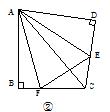

    ∴_________=EF，故DE+BF=EF．
    ⑵方法迁移：
    如图②，将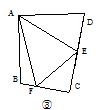沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．

    ⑶问题拓展：
    如图③，在四边形ABCD中，AB=AD，E，F分别为DC,BC上的点，满足,试猜想当∠B与∠D满足什么关系时，可使得DE+BF=EF．请直接写出你的猜想（不必说明理由）．
    思路点拨：在图1中，由于45°、直角等特殊角度，通过旋转△ADE，可形成∠1+∠3=45°，构造三角形全等，从而探究出DE+BF=EF.在图2中，同样存在，可通过旋转△ADE，构建两三角形全等。同理在图3中，要使DE+BF=EF，一定要通过旋转，而实现旋转，必要求点E应旋转到FB的延长线上，即∠B与∠D 互补。
    解：⑴EAF、△EAF、GF．
    ⑵DE+BF=EF，理由如下：
    如图④中，假设∠BAD的度数为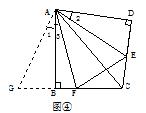，将△ADE绕点A顺时针旋转得到△ABG，此时AB与AD重合，由旋转可得：AB=AD,BG=DE, ∠1=∠2，∠ABG=∠D=90°,

    ∴∠ABG+∠ABF=90°+90°=180°，因此，点G，B，F在同一条直线上．
    ∵∠EAF= ∴∠2+∠3=∠BAD-∠EAF=，
    ∵∠1=∠2，   ∴∠1+∠3=．即∠GAF=∠EAF，又AG=AE，AF=AF，∴△GAF≌△EAF．∴GF=EF，又∵GF=BG+BF=DE+BF， ∴DE+BF=EF．
    ⑶当∠B与∠D互补时，可使得DE+BF=EF．
    点评：此题以阅读理解的形式进行课题学习探究，题目中首先提供某种思路、方法或中间步骤，探讨某种情境或特殊情形下的解题思路与方法，然后将其进行拓展、推广到一般情况，进一步探究相关结论，解答此类问题的基本步骤是阅读——分析——理解——迁移——创新应用。
    三、操作探究类
    例3：（2011江苏苏州）如图①，小慧同学吧一个正三角形纸片（即△OAB）放在直线l₁上，OA边与直线l₁重合，然后将三角形纸片绕着顶点A按顺时针方向旋转120°，此时点O运动到了点O₁处，点B运动到了点B₁处；小慧又将三角形纸片AO₁B₁绕B₁点按顺时针方向旋转120°，点A运动到了点A₁处，点O₁运动到了点O₂处（即顶点O经过上述两次旋转到达O₂处）.
    小慧还发现：三角形纸片在上述两次旋转过程中，顶点O运动所形成的图形是两段圆弧，即弧OO₁和弧O₁O₂，顶点O所经过的路程是这两段圆弧的长度之和，并且这两端圆弧与直线l₁围成的图形面积等于扇形AOO₁的面积、△AO₁B₁的面积和扇形B₁O₁O₂的面积之和.
    小慧进行类比研究：如图②，她把边长为1的正方形纸片OABC放在直线l₂上，OA边与直线l₂重合，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时点O运动到了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₁处；小慧又将正方形纸片AO₁C₁B₁绕B₁点按顺时针方向旋转90°，……，按上述方法经过若干次旋转后，她提出了如下问题：
    问题①：若正方形纸片OABC按上述方法经过3次旋转，求顶点O经过的路程，并求顶点O在此运动过程中所形成的图形与直线l₂围成图形的面积；若正方形OABC按上述方法经过5次旋转，求顶点O经过的路程；
    问题②：正方形纸片OABC按上述方法经过多少次旋转，顶点O经过的路程是π？
    请你解答上述两个问题.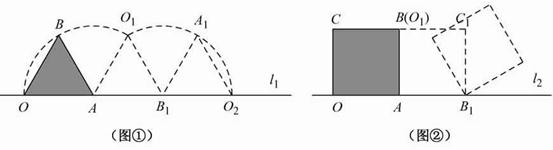

    解析：问题①：如图，正方形纸片OABC经过3次旋转，顶点O运动所形成的图形是三段弧，即弧OO₁、弧O₁O₂以及弧O₂O₃，∴顶点O运动过程中经过的路程为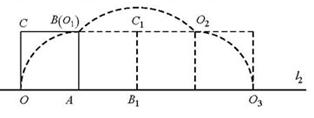
    .

    顶点O在此运动过程中所形成的图形与直线l₂围成图形的面积为
    =1+π.
    正方形OABC经过5次旋转，顶点O经过的路程为.
    问题②：∵方形OABC经过4次旋转，顶点O经过的路程为
    ，∴π=20×π+π.
    ∴正方形纸片OABC经过了81次旋转.
    点评：本题是一道典型的滚动探究与适当作图相结合的实践能力操作题，在解题过程中学生经历了“问题探究——问题解决”的过程，此类动手操作类的课题学习试题的解决策略是：通过对给定的信息进行分析、整理、研究，借助一定的实物操作与理性思考，得出一些有价值的信息与猜想，然后运用平时积累的知识、思想与方法解决问题，得出正确的结论。
    四、课题实验探究类
    例4：（2010江西）课题：两个重叠的正多边型，其中一个绕某一顶点旋转所形成的有关问题．
    实验与论证
    设旋转角∠A₁A₀B₁=α（α< A₁A₀A₂）， θ₃，θ₄，θ₅，θ₆，所表示的角如图所示．

（1）用含α的式子表示角的度数：θ₃=___________θ₄=_____________θ₅=____________

（2）
    （2）图1－图4中，连接A₀H时，在不添加其他辅助线的情况下，是否存在与直线A₀H垂直且被它平分的线段？若存在，请选择期中的一个图给出证明；若不存在，请说明理由；
    归纳与猜想
    设正n边形A₀A₁A₂…A_n_－1与正n边形A₀B₁B₂…B_n_－1重合（其中，A₁与B₁重合），现将正n边形A₀B₁B₂…B_n_－1绕顶点A₀逆时针旋转α（）．
    （3）设θ_n与上述“θ₃，θ₄，…”的意义一样，请直接写出θ_n的度数；
    （4）试猜想在正n边形的情形下，是否存在与直线A₀H垂直且被它平分的线段？若存在，请将这条线段用相应的顶点字母表示出来（不要求证明）；若不存在，请说明理由．

    思路点拨：（1）要求的度数，应从旋转中有关角度的变与不变上突破；（２）结合图形比较容易得到被垂直平分的线段，在证明时要充分利用背景中正多边形及旋转中的角度；（３）要探究的度数，要注意区分正偶数边形及正奇数边形两种情形去思考与求解度数的表达式；（４）要探究正ｎ边形中被垂直平分的线段，只要观察图形的对称性就可以找到解题的途径．也应注意区分正偶数边形及正奇数边形两种情形去思考与突破；
    解：（１）．
    （２）答案不唯一，选图１，图１中有直线垂直平分．
    证明：∵与是全等的等边三角形，∴，∴，∴，∴点在线段的垂直平分线上，所以直线垂直平分．
    （３）当为奇数时，，当为偶数时，．
    （４）存在，当为奇数时，直线垂直平分．
    当为偶数时，直线垂直平分．
    点评：本题以课题学习为背景及方式呈现，通过 “两个重叠的正多边形，其中的一个绕某一顶点旋转所形成的有关问题”的探讨．是研究一个由特殊到一般结论的数学问题，先从简单特殊的几种正多边形入手，再推广到正n边形情形下规律的探究，这种探究思路和类比迁移的数学思想，应引起高度重视与学习．
    五活动探讨类
    例5:（2011江西）某数学兴趣小组开展了一次活动，过程如下：
    设∠BAC=（0°＜＜90°）.现把小棒依次摆放在两射线之间，并使小棒两端分别落在射线AB，AC上.
    活动一：如图甲所示，从点A₁开始，依次向右摆放小棒，使小棒与小棒在端点处互相垂直. （A₁A₂为第1根小棒）
    数学思考：
    （1）小棒能无限摆下去吗？答：          .(填“能”或“不能”)
    （2）设AA₁=A₁A₂=A₂A₃=1.
    ①=_________度；

    ②若记小棒A_2n-1A_2n的长度为a_n（n为正整数，如A₁A₂=a₁，A₃A₄=a₂，…），求出此时a₂，a₃的值，并直接写出a_n（用含n的式子表示）.
    活动二：如图乙所示，从点A₁开始，用等长的小棒依次向右摆放，其中A₁A₂为第一根小棒，且A₁A₂=AA₁.

    数学思考：
    （3）若已经摆放了3根小棒，则₁ =_________，₂=________， ₃=________；（用含的式子表示）

    （4）若只能摆放4根小棒，求的范围.
    思路点拨:在活动一中,由于摆放的小棒依次互相垂直,不断构建内错角相等,故能不断摆放；在等腰△A₂A₃A₁中,由勾股定理得A₃A₁=，借助平行,可知平行所截的三角形相似,运用比例线段可依次求得a₁，a₂，…a_n,在活动二中,在依次摆放等腰三角形的过程中,利用三角形的外角可依次求得₁，₂， ₃与的关系, 若只能摆放4根小棒,说明以₃为等腰三角形的底角的度数不能超过90°,而以₄为三角形的外角必不小于90°,从而构建不等式组求解的取值范围.
    解: (1)能．
    (2)① 22.5°.
    ②∵A A₁=A₁A₂=A₂A₃=1，A₁A₂⊥A₂A₃， ∴A₁A₃=，AA₃=.又∵A₂A₃⊥A₃A₄，∴A₁A₂∥A₃A₄.
    同理：A₃A₄∥A₅A₆.∴∠A₂A₃A₄=∠A₄A₅A₆=90°，∠A₂A₄A₃=∠A₄ A₆A₅，∴△A₂A₃A₄∽△A₄A₅A₆，
    ∴，∴a₃=.
    (3), ,
    (4)由题意得： ∴.
    点评: 本题以一个普通角为背景，创设摆放小棒的数学活动：搭建直角三角形与等腰三角形，开展课题研究，让学生感到熟悉而亲切，同学们都能在一定程度上得分，通过一系列问题的设问，将初中阶段的核心知识（等腰三角形、直角三角形、相似三角形、不等式组等）巧妙融入其中进行思考与探究，区分度与综合度明显增强。为此要求我们在日常教学中，应时刻关注身边的数学素材，注重开展与之相关的数学活动与数学研究，以提高学生的分析与探究能力。
    课题学习类试题通常以探索、研究、实验操作等不同形式呈现于中考中，并借助恰当的数学素材，作为试题的内容和明确的研究方向；或是以几何图形为题材，或是以数学问题为背景等；通过对相关问题的描述或逐步观察、操作（包括数据分析、整理、运算或作图、或证明）和归纳、探究等，进而发现问题，创新问题．试题在注重考查相关基础知识、基本技能、方法的同时，更注重考查对相关知识的联想、探索、发现、总结归纳及创新的能力．是近几年中考改革中出现的新题型．一般包含：课题的提出、数学模型的建立、问题的解决、数学知识的应用、酝酿与形成研究问题的方法． (责任编辑：admin)

搜索

热门标签:

中考课题学习的酝酿与探究