|
学联想 找证法 助复习 湖北省黄石市下陆中学 周国强 宋毓彬 证明几何题的苦恼莫过于思路不清，现以课本中的一道习题为例，从多角度进行思维得到几种巧妙证法，供忙于中考复习的同学参考。 已知  ：⊙O 和⊙O 相交于点C和D ，OO的延长线和⊙O相交于点A，AC，AD分别和⊙O相交于点E，F。求证：CE=DF。（人教版几何第三册P B组第1题）一、考虑到线段的和差关系 证法1：连CD（如图1），则CD⊥O  且CP＝DP（连心线垂直平分公共弦）∴AC＝AD（1）（线段中垂线上的点到线段两端的距离相等） 由切割线定理的推论知，AC×AE＝AD×AF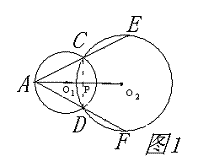，  ∴AE＝AF（2）， （2）－（1）得：CE＝DF。 注：遇两圆相交，常连公共弦 二、考虑到同圆中等弧对等弦 证法2：如图1，由证法1，知 AC=AD， ∴ ∠ACD＝∠ADC， 从而∠ECD＝∠FDC。 ∴  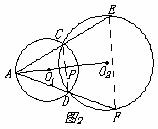＝ （同圆中相等的圆周角所对的弧相等） ∴  － ＝ － ，即 ＝ ， 故CE＝DF。（同圆中等弧对等弦） 注：同圆中，利用弧相等来证明弦相等是常用的方法之 三、 考虑到同圆中平行弦所夹的同名弧相等 证法３：连ＣＤ，ＥＦ（如图２）。 由证法2知∠ACD＝∠ADC， ∵∠ACD＝∠F，∠ADC＝∠E，（圆内接四边形的对角相等） ∴∠E＝∠ACD， ∴CD∥EF， ∴  ，(同圆中平行弦所夹的弧相等)故CE=DF。 注：同名弧：即优弧与优弧，劣弧与劣弧。 四、考虑到同圆中相等的弦心距对应的弦相等 证法4：连CD，作O 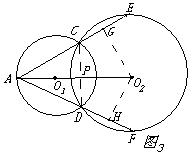G⊥ＣＥ于Ｇ，OＨ⊥DF于H（如图3） 由证法1知AC=AD，∴∠CAP=∠DAP 即AO 平分∠EAF，∴OG＝OH，(角平分线上的点到角的两边距离相等)故 CE＝DF。（同圆中相等的弦心距所对应的弦相等） 注：同圆中，如果两个圆心角，两条弧，两条弦及这两条弦的弦心距这四组量中有一组量相等，那么其余三组量也分别相等。证法1、证法2、证法3的出发点都是基于这条推论。(能否利用圆心角相等来证明本题中的结论呢？同学们不妨一试。) 五、考虑到圆的对称性 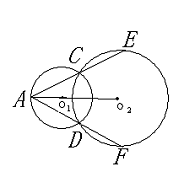  证法5：如图4，因为连心线OO是两圆的对称轴，A在 OO上，C，D为两圆的交点，E，F分别是AC，AD的延长线与⊙O的交点，所以点C与点D，点E与点F均关于连心线OO对称，从而线段CE与DF关于直线OO对称，故CE＝DF。（轴对称的线段是相等的线段）由此可见，根据题目所给的条件，结合图形的特点，联想课本中的有关定理（推论）性质等，容易找到解决问题的基本途径，从而提高复习效率。 练习：如图，梯形ABCD中，AB⊥BC，以AD为直径的⊙O交AB于N，切BC于M。 求证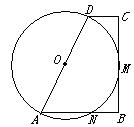：   (提示：本题不少于五种证法) (责任编辑：admin) |