中考中的一次函数应用题求解策略
湖北省黄市市下陆中学 宋毓彬
1 试题概述
一次函数应用题,因其综合了一元一次方程、一元一次不等式、二元一次方程组等内容,能实现数与形有机地结合,能体现分类讨论、对应、极端值等数学思想与方法,并且容易与现实生活中的重大事件联系起来以体现数学的应用价值,近年来一直是中考命题的热点。此外,由于中考考查二次函数内容时,大多是以二次函数与几何相结合的压轴题形式出现,而反比例函数应用题命题的范围又相对狭窄,因此一次函数应用题就一直是中考试题中最频繁出现的考点。
一次函数应用题考查的最主要考点集中在三个方面:⑴学生对数形结合的认识和理解;⑵将实际问题转化为一次函数的能力,即数学建模能力;⑶分类讨论、极端值、对应关系、有序性的数学思想方法的考查。⑷对一次函数与方程、不等式关系的理解与转化能力。
一次函数试题的命题形式多样,从近几年的中考题来看,可以大致归为以下几类:⑴方案设计问题(物资调运、方案比较);⑵分段函数问题(分段价格、几何动点);⑶由形求式(单个函数图象、多个函数图象)。⑷一次函数多种变量及其最值问题。
2 试题例析
2.1方案设计问题
⑴物资调运
例1.(2008年重庆第27题)为支持四川抗震救灾,重庆市A、B、C三地现在分别有赈灾物资100吨,、100吨、80吨,需要全部运往四川重灾地区的D、E两县。根据灾区的情况,这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨。
(1)求这批赈灾物资运往D、E两县的数量各是多少?
(2)若要求C地运往D县的赈灾物资为60吨,A地运往D的赈灾物资为x吨(x为整数),B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍。其余的赈灾物资全部运往E县,且B地运往E县的赈灾物资数量不超过25吨。则A、B两地的赈灾物资运往D、E两县的方案有几种?请你写出具体的运送方案;
(3)已知A、B、C三地的赈灾物资运往D、E两县的费用如下表:
|
A地
|
B地
|
C地
|
运往D县的费用(元/吨)
|
220
|
200
|
200
|
运往E县的费用(元/吨)
|
250
|
220
|
210
|
为即使将这批赈灾物资运往D、E两县,某公司主动承担运送这批赈灾物资的总费用,在(2)问的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?
解析:本题题干文字长,数量关系复杂,但只要弄懂了题意,并结合表格将数量关系进行整理,解决起来并不难。
⑴直接用一元一次方程求解。运往D县的数量比运往E县的数量的2倍少20吨,设运往E县m吨,则运往D县(2m-20)吨,则m+(2m-20)=280,m=100,2m-20=180。(亦可用二元一次方程组求解)
⑵由⑴中结论,并结合题设条件,由A地运往D的赈灾物资为x吨,可将相应数量关系列表如下:
|
A地(100吨)
|
B(100吨)
|
C(80吨)
|
D县(180吨)
|
x(220元/吨)
|
180-60-x
=120-x(200元/吨)
|
60(200元/吨)
|
E县(100吨)
|
100-x(250/吨元)
|
100-20-(100-x)
=x-20(220元/吨)
|
20(210元/吨)
|
表格说明:①A、B、C、D、E各地后括号中的数字为调运量或需求量;
②表格中含x的式子或数字,表示对应地点调运数量;
③表格中其他括号中的数字,表示对应的调运费用。
确定调运方案,需看问题中的限制条件:①B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍。②B地运往E县的赈灾物资数量不超过25吨。故:
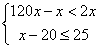 解得 解得 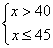 ∴40<x≤45 ∵x为整数 ∴40<x≤45 ∵x为整数
∴x的取值为41,42,43,44,45 则这批救灾物资的运送方案有五种。
方案一:A县救灾物资运往D县41吨,运往E县59吨;
B县救灾物资运往D县79吨,运往E县21吨。 (其余方案略)
⑶设运送这批赈灾物资的总费用为y,由⑵中表格可知:
y=220x+250(100-x)+200(120-x)+220(x-20)+200×60+210×20
=-10x+60800
∵y随x增大而减小,且40<x≤45,x为整数,
∴当x=41时,y有最大值。
该公司承担运送这批赈灾物资的总费用最多是:y=-10×41+60800=60390(元)
求解物资调运问题的一般策略:
⑴用表格设置未知数,同时在表格中标记相关数量;
⑵根据表格中量的关系写函数式;
⑶依题意正确确定自变量的取值范围(一般通过不等式、不等式组确定);
⑷根据函数式及自变量的取值范围,结合一次函数的性质,按题设要求确定调运方案。
物资调运问题应用广泛,包括调水、调运物资、分配物资等多种类型。
⑵方案比较
例2.(2008年盐城)在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元)。现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购买门票的价格为每张60元;(总费用=广告赞助费+门票费)
方案二:购买方式如图2所示。
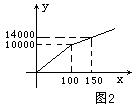
解答下列问题:
⑴方案一中,y与x的函数关系式为 ;方案二中,当0≤x≤100时,y与x的函数关系式为 ,当x>100时,y与x的函数关系式为 。
⑵如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由。
⑶甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张?
解析:这是一个两种方案的比较问题。方案比较通常与不等式联系紧密。比较优惠条件,即通过比较函数值的大小,确定自变量的区间。
⑴中方案一的函数关系式,直接依题意写出:y1=60x+10000(x≥0);方案二的函数关系由图象给出,用待定系数法求解。当0≤x≤100时,图象为过原点的线段,函数式为正比例函数,可求得y2=100x(0≤x≤100);当x>100时,图象为不过原点的射线,函数式为一次函数,过(100,10000),(150,14000),可求得y2=80x+2000(x>100)。
⑵购买门票超过100张,比较那种方案最省,了先使y1=y2,求出此时x的值。然后利用不等式确定方案。
当y1=y2时,60x+10000=80x+2000,解得x=400,即购买400张门票,两种方案费用相同。
当y1>y2时,解得x<400,则当100<x<400时,选择方案二,总费用最省;
当y1<y2时,解得x>400,则当x>400时,选择方案一,总费用最省。
⑶分两种情况讨论:(用方程求解)
①甲单位按方案购买的门票少于100张时,设甲买m(m<100)张,则乙买700-m张。
100m+60(700-m)+10000=58000 解得m=150(不合题意,舍去)
②甲单位按方案购买的门票少于100张时,设甲买m(m>100)张,则乙买700-m张
80m+2000+60(700-m)+10000=58000 解得m=200,700-m=500
求解方案比较问题的一般策略:
⑴在方案比较问题中,不同的方案有不同的函数式。因此首先需设法求出不同方案各自的函数式。求函数式时,有图象的,多用待定系数法求;没有给出图象的,直接依题意进行列式。
⑵方案比较问题通常都与不等式、方程相联系。比较方案,即比较同一自变量所对应的函数值。要会将函数问题转化为方程、不等式问题。
⑶方案比较中尤其要注意不同的区间,多对应的大小关系不同。
方案比较问题,在门票、购物、收费、设计等问题中都可涉及。
2.2分段函数问题
⑴分段价格
例3.(2008年襄樊第23题)我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费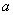 元;一月用水超过10吨的用户,10吨水仍按每吨 元;一月用水超过10吨的用户,10吨水仍按每吨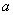 元收费,超过10吨的部分,按每吨 元收费,超过10吨的部分,按每吨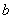 元(b>a)收费.设一户居民月用水 元(b>a)收费.设一户居民月用水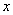 吨,应收水费 吨,应收水费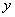 元, 元,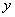 与 与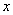 之间的函数关系如图13所示. 之间的函数关系如图13所示.
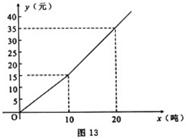
(1)求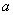 的值;某户居民上月用水8吨,应收水费多少元? 的值;某户居民上月用水8吨,应收水费多少元?
(2)求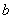 的值,并写出当x>10时, 的值,并写出当x>10时,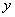 与 与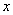 之间的函数关系式; 之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
解析:(1)当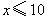 时,有 时,有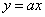 .将 .将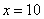 , ,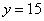 代入,得 代入,得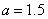 . .
用8吨水应收水费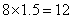 (元). (元).
(2)当x>10时,有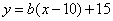 . 将 . 将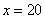 , ,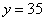 代入, 代入,
得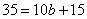 ∴ ∴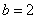 . 故当x>10时, . 故当x>10时,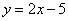 . .
(3)因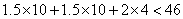 , ,
所以甲、乙两家上月用水均超过10吨.
设甲、乙两家上月用水分别为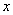 吨, 吨,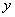 吨, 吨,
则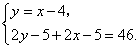 解之,得 解之,得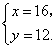
故居民甲上月用水16吨,居民乙上月用水12吨.
解分段价格问题的一般策略:
⑴分段函数的特征是:不同的自变量区间所对应的函数式不同,其函数图象是一个折线。解决分段函数问题,关键是要与所在的区间相对应。
⑵分段函数中“折点”既是两段函数的分界点,同时又分别在两段函数上。在求解析式要用好“折点”坐标,同时在分析图象时还要注意“折点”表示的实际意义,“折点”的纵坐标通常是不同区间的最值。
⑶分段函数应用广泛,在收费问题、行程问题及几何动态问题中都有应用。
⑵几何图形中的动点
例4.(2008年长沙第25题)在平面直角坐标系中,一动点P(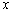 ,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动。图②是P点运动的路程s(个单位)与运动时间 ,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动。图②是P点运动的路程s(个单位)与运动时间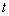 (秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分. (秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
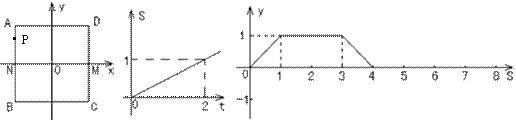 
(图①) (图②) (图③)
(1)s与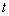 之间的函数关系式是: ; 之间的函数关系式是: ;
(2)与图③相对应的P点的运动路径是: ;P点出发 秒首次到达点B;
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图③中补全函数图象.
解析:(1)由图象可知为正比例函数。S=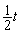 (t≥0) (2)由图象③,M纵坐标为0变为1,则路径为:M→D→A→N, 10秒 (t≥0) (2)由图象③,M纵坐标为0变为1,则路径为:M→D→A→N, 10秒
(3)当3≤s<5,即P从A到B时,y=4-s;
当5≤s<7,即P从B到C时,y=-1;
当7≤s≤8,即P从C到M时,y=s-8.(补全图象略.)
求解几何图形中的动点问题一般策略:
⑴解决几何图形中的动态问题,关键是看动点运动的路径,在不同的路径上,所对应的线段长(高)等不同,由此引起其它变量的变化。因此根据不同路径以确定自变量的变化区间至关重要。
⑵在不同的区间上求函数表达式,应注意紧密结合几何图形的特征,会将将函数中的变量关系转化为几何图形上的对应线段关系。
⑶动点(动线)问题,引起图形中相关量的变化,多以面积为主。本题给出的坐标变化相对降低了难度。但给出的图象较多,涉及到路程与时间、路程与坐标三个变量,共两种函数,在解决问题时,应认真审题。
2.3数形结合由“形”求式
⑴单个函数图象
例5.(2008年南京)28.(10分)一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为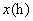 ,两车之间的距离为 ,两车之间的距离为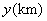 ,图中的折线表示 ,图中的折线表示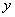 与 与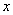 之间的函数关系. 之间的函数关系.
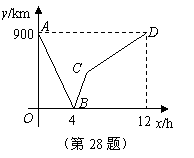 
根据图象进行以下探究:
信息读取
(1)甲、乙两地之间的距离为 km;
(2)请解释图中点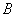 的实际意义; 的实际意义;
图象理解
(3)求慢车和快车的速度;
(4)求线段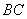 所表示的 所表示的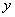 与 与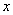 之间的函数关系式,并写出自变量 之间的函数关系式,并写出自变量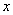 的取值范围; 的取值范围;
问题解决
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
解析:(1)900; (2)图中点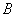 的实际意义是:当慢车行驶4h时,慢车和快车相遇. 的实际意义是:当慢车行驶4h时,慢车和快车相遇.
(3)由图象可知,慢车12h行驶的路程为900km,所以慢车的速度为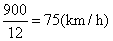 ; ;
当慢车行驶4h时,慢车和快车相遇,两车行驶的路程之和为900km,所以慢车和快车行驶的速度之和为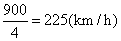 ,所以快车的速度为150km/h. ,所以快车的速度为150km/h.
(4)根据题意,快车行驶900km到达乙地,所以快车行驶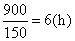 到达乙地,此时两车之间的距离为 到达乙地,此时两车之间的距离为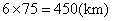 ,所以点 ,所以点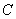 的坐标为 的坐标为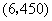 . .
设线段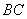 所表示的 所表示的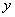 与 与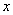 之间的函数关系式为 之间的函数关系式为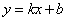 ,把 ,把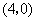 , ,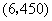 代入得 代入得
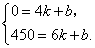 解得 解得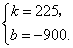
所以,线段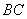 所表示的 所表示的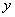 与 与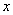 之间的函数关系式为 之间的函数关系式为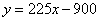 . .
自变量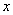 的取值范围是 的取值范围是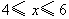 . .
(5)慢车与第一列快车相遇30分钟后与第二列快车相遇,此时,慢车的行驶时间是4.5h.
把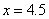 代入 代入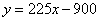 ,得 ,得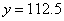 . .
此时,慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km,所以两列快车出发的间隔时间是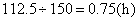 ,即第二列快车比第一列快车晚出发0.75h. ,即第二列快车比第一列快车晚出发0.75h.
单个函数图象求“式”的一般策略:
⑴单个函数图象,尤其是折线图,在读图过程中一定要正确认识和理解图形上点的坐标的实际意义。
⑵要关注“折点”所表示的意义,用好折点坐标。
⑶用图象求函数式,多用待定系数法,因此要善于寻找图象上点的坐标。一方面可以从图象上寻找,此外还可以结合题设中的条件寻找。
⑵多个函数图象
例6 (2008年泰州第28题)2008年5月12日14时28分四川汶川发生里氏8.0级强力地震。某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区。乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时)。图中的折线、线段分别表示甲、乙两组所走路程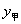 (千米)、 (千米)、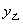 (千米)与时间x(小时)之间的函数关系对应的图像。请根据图像所提供的信息,解决下列问题: (千米)与时间x(小时)之间的函数关系对应的图像。请根据图像所提供的信息,解决下列问题:
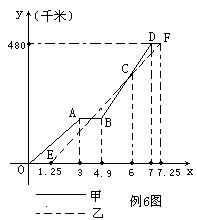
(1)由于汽车发生故障,甲组在途中停留了_________小时;(2分)
(2)甲组的汽车排除故障后,立即提速赶往灾区。请问甲组的汽车在排除故障时,距出发点的路程是多少千米?(6分)
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不过25千米。请通过计算说明,按图像所表示的走法是否符合约定。
解析:本题由甲乙两个互相关联但又不同的行程问题构成,函数图象之间彼此相交。要解决好所求问题,必须深入认识和理解图象中的信息,尤其是已知点坐标的实际意义。
(1)由图象可知:AB段发生故障。时间为4.9-3=1.9 (小时)
(2)要求甲组的汽车在排除故障时,距出发点的路程是多少千米。即要求出B点的纵坐标。点B在线段BD上,且横坐标为4.9。只需求出BD所在直线的解析式即可。C是BD、EF交点,C点的横坐标为6,求出直线EF的解析式,则可得到C点坐标。从而求出BD解析式,得到B点纵坐标。
设直线EF的解析式为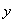 乙=kx+b∵点E(1.25,0)、点F(7.25,480)均在直线EF上 乙=kx+b∵点E(1.25,0)、点F(7.25,480)均在直线EF上
∴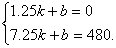 解得 解得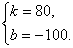 ∴直线EF的解析式是y乙=80X-100 ∴直线EF的解析式是y乙=80X-100
∵点C在直线EF上,且点C的横坐标为6,
∴点C的纵坐标为80×6—100=380 ∴点C的坐标是(6,380)
设直线BD的解析式为y甲 = mx+n
∵点C(6,380)、点D(7,480)在直线BD上
∴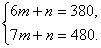 解得 解得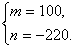 ∴BD的解析式是y甲=100X -220 ∴BD的解析式是y甲=100X -220
∵B点在直线BD上且点B的横坐标为4.9,代入y甲得B(4.9,270)
∴甲组在排除故障时,距出发点的路程是270千米。
(3)符合约定
由图像可知:甲、乙两组第一次相遇后在B和D相距最远。
在点B处有y乙—y甲=80×4.9—100—(100×4.9—220)=22千米<25千米
在点D有y甲—y乙=100×7—220—(80×7—100)=20千米<25千米
∴按图像所表示的走法符合约定
多个函数图象求式问题的一般策略:
⑴一题中有多个函数图象时,尤其要关注图象交点的坐标。因其交点坐标同时满足两个图象的关系式。
⑵分析多个函数图象时,还应关注其交点两侧图象的上下位置关系。图象在上方的函数图象,同一个自变量所对应的函数值大。由此可比较两个函数图象所表示函数式之间的变化关系。
2.4多变量及其最值问题
例7(2008年泰安第25题)某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数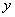 (亩)与补贴数额 (亩)与补贴数额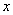 (元)之间大致满足如图1所示的一次函数关系.随着补贴数额 (元)之间大致满足如图1所示的一次函数关系.随着补贴数额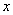 的不断增大,出口量也不断增加,但每亩蔬菜的收益 的不断增大,出口量也不断增加,但每亩蔬菜的收益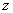 (元)会相应降低,且 (元)会相应降低,且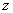 与 与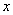 之间也大致满足如图2所示的一次函数关系. 之间也大致满足如图2所示的一次函数关系.
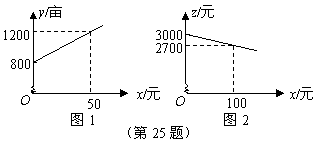 
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数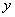 和每亩蔬菜的收益 和每亩蔬菜的收益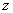 与政府补贴数额 与政府补贴数额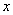 之间的函数关系式; 之间的函数关系式;
(3)要使全市这种蔬菜的总收益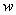 (元)最大,政府应将每亩补贴数额 (元)最大,政府应将每亩补贴数额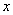 定为多少?并求出总收益 定为多少?并求出总收益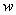 的最大值. 的最大值.
解析:(1)政府没出台补贴政策前,这种蔬菜的收益额为: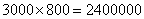 (元) (元)
(2)由题意可设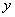 与 与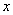 的函数关系为 的函数关系为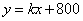 将 将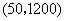 代入上式 代入上式
得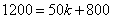 ∴ ∴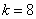 ∴种植亩数与政府补贴的函数关系为 ∴种植亩数与政府补贴的函数关系为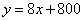
同理可得,每亩蔬菜的收益与政府补贴的函数关系为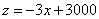
(3)由题意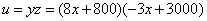 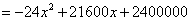
∴u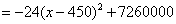
∴当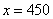 ,即政府每亩补贴450元时,全市的总收益额最大,最大为7260000元. ,即政府每亩补贴450元时,全市的总收益额最大,最大为7260000元.
解多个变量及其最值问题的一般策略:
⑴一个问题中涉及多个变量,往往对应着多个函数式。因此在求解过程中,一定要理清变量之间的对应关系,正确求出不同的函数式。
⑵求函数的最值问题,一次函数主要运用一次函数性质求。二次函数则可用配方法或公式法求。
⑶对于函数式的求取,则主要是用列式法和待定系数法。
作者简介:宋毓彬,男,44岁,中学数学高级教师。在《中学数学教学参考》、《中学数学》、《中学生数学》、《数理天地》、《数理化学习》、《数理化解题研究》、《中学课程辅导》、《数学周报》、《数学辅导报》、《数理报》、《少年智力开发报》、《学习报》、《小博士报》等报刊发表教学辅导类文章70多篇。主要致力于初中数学中考及解题方法、技巧等教学方面的研究。
(责任编辑:admin) |