|
☆☆☆ 点击下载试题 ☆☆☆ 请点击全屏查看 2016襄阳市中考数学模拟试题 数 学 试 题 （本试卷共4页，满分120分） ★祝考试顺利★
一、选择题（本大题共10个小题，每小题3分，共30分）在每小题给出的四个选项中，只有一项是符合题目要求的，请将序号在答题卡上涂黑作答． 1．  的倒数的相反数是（▲）A．  B． C． D． 2．（2016襄阳数学）人体血液中每个成熟红细胞的平均直径为0.0000077米，用科学记数法表示为（▲） A．7.7×10﹣5米 B．7.7×10﹣6米 C．77×10﹣5米 D．7.7×10﹣7米 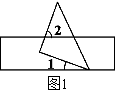 3．如图1，把一块等腰直角三角板的锐角顶点放在直尺的一边上，如果∠1＝20°，那么这个锐角所对的直角边与直尺的另一边相交所得的∠2的度数是（▲）A．60° B．65° C．70° D．80° 4．下列说法正确的是（▲） A．掷一枚质地均匀的骰子，“向上一面的点数是6”是必然事件 B．了解一批电视机的使用寿命，适合用普查的方式 C．“明天降雨的概率为  ”，表示明天有半天都在降雨D．在统计中，样本的方差可以近似地反映总体的波动大小 5．下列几何图形中，既是轴对称图形又是中心对称图形的是（▲） A．等腰三角形 B．等边三角形  C．菱形 D．正五边形6．（2016襄阳数学）  如下左图是由几个小立方块所搭成的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，则这个几何体的左视图为（▲） A． B． C． D． 7．有四个式子：①  ；② ；③ ；④ ，从这四个式子中 随机抽取一个，抽到的式子不正确的概率是（▲）A．  B． C． D． 8．已知关于 x的不等式组 有且只有1个整数解，则a的取值范围是（▲）A．a＞1 B．1≤a＜2 C．1＜a≤2 D  ．a≤29．射线AD、AE分别与⊙O相切于D、E两点，直线BC与⊙O相切于点F，分别交AD、AE于点B、C，若∠A＝40°．则∠BOC等于（▲） A．70° B．110° C．70°或110° D．40°或140°  10．（2016襄阳数学）如图2，在平面直角坐标系中，A（0， ），B（6，0），点P 为线段AB的中点，将线段AB绕点O逆时针旋转 90°后点P的对应点P/的坐标是（▲） A．（－3，  ） B．（ ，3）C．（  ，－3） D．（－1，）二、填空题（本大题共6个小题，每小题3分，共18分）把答案填在答题卡的相应位置上． 11．在函数  中，自变量x的取值范围是 ▲ ．[来源:Zxxk.Com]12．从1，2，3，5这四个数中任取三个不同的数，其和为偶数的概率是 ▲ ． 13．已知关于x的方程 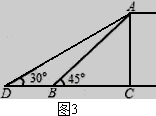 的解是负数，则m的取值范围是 ▲ ． 14．用半径为3cm，圆心角是120°的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为 ▲ cm．15．某处欲建一观景平台，如图3所示，原设计平台的楼梯长AB＝6m，∠ABC＝45 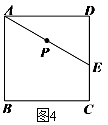°，后考虑到安全因素，将楼梯脚B移到CB延长线上点D处，使∠ADC＝30°，则调整后楼梯AD的长为 ▲ m．（结果保留根号） 16．如图4，E为正方形ABCD中CD边上一点，∠DAE＝30°，P为AE的中点，过点P作直线分别与AD、BC相交于点M、N．若MN＝AE，则∠AMN等于 ▲ ．三、（2016襄阳数学）解答题（本大题共9个小题，共72分．解答应写出文字说明、证明过程或演算步骤，并且写在答题卡上每题对应的答题区域内．） 17．(本小题满分6分) 先化简，再求值：  ，其中x满足x2＋2x－3＝0．18．(本小题满分6分) 我市今年共种植甲乙两种作物8万亩，甲乙的种植面积分别比去年增长10%和20%，去年甲种作物的种植面积比乙种作物的种植面积多1万亩．今年这两种作物的种植面积各是多少万亩？ 19．(本小题满分6分) 一次函数y1＝x－1与反比例函数  图象的一个交点为A（－1，m ）．（1）求k和m的值； （2）判断点B（2，1）是否为这两个函数图象的一个交点，并说明理由； （3）当y1＞y2时，请直接写出y2的范围． 20．(本小题满分6分) 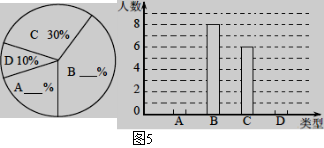 某课外活动小组的同学组织了一次陶艺制作活动，最少的制作了4件作品，最多的制作了7件作品，活动结束后根据每人作品数量，分为四种类型，A：4件；B：5件；C：6件；D：7件．将各类的人数绘制成如图5所示的不完整的扇形图和条形图．请结合图形完成下列问题：（1）这个活动小组共有 人，并补全条形统计图； （2）该小组每人制作陶艺作品数量的中位数是 件，平均数是 件； （3）活动制作对象是茶杯和茶壶，每个人可随机选择制作对象，且每种制作对象被选中的可能性相同，甲乙丙三人制作的第一件作品是同一个对象的概率是 ．  21．（2016襄阳数学）(本小题满分6分)如图6，△ABC中，AB＝AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE＝OD，连接AE，BE．[来源:Z&xx&k.Com] （1）求证：四边形AEBD是矩形； （2）当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由． 22．(本小题满分8分)  如图7，AB是⊙O的直径，D是的中点，弦AC与弦BD交于点E，点F在BD的延长线上，且DF＝DE．（1）求证：AF是⊙O的切线； （2）若AD＝5，AC＝8，求⊙O的半径． 23．（2016襄阳数学）(本小题满分10分) 某商场销售一种成本为每件30元的商品，销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似看作一次函数y＝－10x＋600，商场销售该商品每月获得利润为w（元）． （1）求w与x之间的函数关系式； （2）如果商场销售该商品每月想要获得2000元的利润，那么每月成本至少多少元？ （3）为了保护环境，政府部门要求用更加环保的新产品替代该商品，商场销售新产品，每月的销量与销售价格之间的关系与原产品的销售情况相同，新产品的成本每件32元，若新产品每月的销售量不低于200件时，政府部门给予每件4元的补贴，试求定价多少时，每月销售新产品的利润最大？求出最大的利润．  24．(本小题满分11分)如图8，AD、BE是△ABC的两条高，过点D作DF⊥AB，垂足为F，FD交BE于M，FD、AC的延长线交于点N． （1）求证：△BFM∽△NFA； （2）试探究线段FM、DF、FN之间的数量关系，并证明你的结论； （3）若AC＝BC，DN＝12，  ，求线段AC的长．25．(本小题满分13分)  如图9，已知抛物线y＝ax2＋c与直线 交于A，B两点，直线AB与y轴交于点C，点B的坐标为（1， ），动点P在直线AB下方的抛物线上，动点Q在y轴上，动点D在线段AB上，且PD∥y轴．（1）求A、C两点的坐标及抛物线的解析式； （2）求点P到直线AB的距离的最大值； （3）是否存在以P、Q、C、D为顶点的四边形为菱形？若存在，请直接写出P、Q的坐标；若不存在，请说明理由． 2016襄阳数学答案 一、选择题 1——5：ABCDC 6——10：DCBCB 二、填空题 11、  ；12、 ；13、 且 ；14、1；15、 ；16、60°或120°三、解答题 17、解：原式＝  …………………………………………2分＝  ………………………………………………………3分＝  …………………………………………………………………4分由x2＋2x－3＝0解得，x 1＝－3，x 2＝1………………………………………5分 ∵x≠1 ∴当x ＝－3时，原式＝  …………………………………6分18、解：设去年甲种作物的种植面积为x万亩，乙种作物的种植面积为y万亩 根据题意，得  …………………………………3分解得  ………………………………………………………………………5分（1+10%）x＝4.4（万亩），8－4.4＝3.6（万亩） 答：今年种植甲种作物4.4万亩，种植乙种作物3.6万亩……………………6分 19、解：（1）根据题意，得m＝－1－1＝－2，k＝（－1）×（－2）＝2………2分 （2）∵当x＝2时，y1＝x－1＝1，∴点B在y1＝x－1的图象上……………3分 ∵当x＝2时，  ，∴点B在 的图象上[来源:学*科*网]∴点B（2，1）是这两个函数图象的一个交点…………………………4分 （3）当y1＞y2时，y2＜－2或0＜y2＜1……………………………………6分 20、（2016襄阳数学）解：（1）共有20人；…………………………………………………………1分 A：4人； D：2人………………………………………………………2分 （2）中位数5件；平均数5.3件………………………………………………4分 （3）概率是  ……………………………………………………………………6分21、解：（1）证明：∵点O为AB的中点，点E在DO延长线上，OE＝OD ∴四边形AEBD是平行四边形……………………………………………1分 ∵AB＝AC，AD是△ABC的角平分线 ∴AD⊥BC ∴∠ADB＝90°………………………………………………………………2分 ∴□AEBD是矩形…………………………………………………………3分 （2）当∠BAC＝90°时，矩形AEBD是正方形…………………………4分  理由：∵ AB＝AC，AD是△ABC的角平分线∴AD是△ABC的中线 ∵∠BA  C＝90°∴CD＝BD＝AD……………………………………………………………5分 ∵四边形AEBD是矩形 ∴矩形AEBD是正方形……………………………………………………6分 22、解：（1）证明：∵AB是⊙O的直径 ∴∠ADB＝90°………………………………………………………………1分 ∴AD⊥EF，∠BAD＋∠B＝90° 又∵DF＝DE ∴AF＝AE ∴∠FAD＝∠EAD…………………………………………………………2分 ∵D是的中点 ∴＝ ∴∠FAD＝∠EAD＝∠B……………………………………  ………………3分∴∠FAB＝∠FAD＋∠BAD＝∠BAD＋∠B＝90° 又∵AB是⊙O的直径 ∴AF是⊙O的切线…………………………………………………………4分 （2）作DM⊥AC于M ∵＝ ∴AD＝CD＝5………………………………………………………………5分[来源:Z。xx。k.Com] ∴AM＝CM＝  AC＝4在Rt△DMC中，  ， ……6分∵∠B＝∠C ∴  ∵∠ADB＝90° ∴  …………………………………………………………7分∴⊙O的半径为  …………………………………………………………8分23、解：（1）w＝（x－30)(－10x＋600)＝－10x2＋900x－18000………………2分 （2）由题意得，－10x2＋900x－18000＝2000 解得x1＝40，x2＝50……………………………………………………………4分 当x＝40时，成本为30×（－10×40＋600）＝6000（元） 当x＝50时，成本为30×（－10×50＋600）＝3000（元） ∴每月想要获得2000元的利润，每月成本至少3000元……………………6分 （3）当y＜200时，－10x＋600＜200，解得x＞40 w＝(x－32)(－10x＋600)＝－10（x－46）2＋1960 ∵a＝－10＜0，x＞40，∴当x＝46时，w最大值＝1960(元) ………………7分 当y≥200时，－10x＋600≥200，解得x≤40 w＝（x－32＋4)(－10x＋600)＝－10（x－44）2＋2560…………  …………8分∵a＝－10＜0，∴抛物线开口向下,当32＜x≤40时，w随x的增大而增大 ∴当x＝40时，w最大值＝2400(元) ……………………………………………9分 ∵1960＜2400，∴当x＝40时，w最大 ∴定价每件4  0元时，每月销售新产品的利润最大，最大利润为2400元…10分24、（2016襄阳数学）解：（1）证明：∵DF⊥AB，AD、BE是△ABC的高 ∴∠BFD＝∠AFD＝∠AEB＝∠ADB＝90°……………………………………1分 ∴∠FBM＝90°－∠BAC，∠N＝90°－∠BAC ∴∠FBM＝∠N……………………………………………………………………2分 ∵∠FBM＝∠N，∠BFD＝ ∠AFD∴△BFM∽△NFA…………………………………………………………………3分 （2）DF2＝FM·FN………………………………………………………………4  分证明：∵△BFM∽△NFA ∴  ，∴ ………………………………………5分∵∠FBD＋∠FDB＝90°，∠FBD＋∠FAD＝90°， ∴∠FDB＝∠FAD ∵∠BFD＝∠AFD，∠FDB＝∠FAD，∴△BFD∽△DFA……………………6分 ∴  ， ∴DF2＝FM·FN…………………………………………………………………7分 （3）∵AC＝BC，∴∠BAC＝∠ABC ∵ ∠ABC＋∠FDB＝∠BAC＋∠N＝90° ∴∠FDB＝∠N＝∠FBM ∴  ，  ∴FB＝2FM，FD＝2FB＝4FM…………………………………………………8分 ∵DF2＝FM·FN，∴（4FM）2＝FM·（4FM＋12） 解得FM＝1或F M＝0（舍去）…………………………………………………9分∴FB＝2，FD＝4，FN＝FD＋DN＝16 ∵  ∴AF＝8，AB＝AF＋BF＝10……………………………………………………10分 在Rt△BFD中，  在Rt△ADB和Rt△ADC中，AD2＝AB2－BD2＝AC2－CD2 ∴  解得  ………………………………………………………………………11分25、（2016襄阳数学）解：（1）由  ，解得 ，所以点A的坐标为（－4，0）…1分当  时， ，所以点C的坐标为（0，－3）………………2分 将A、B两点坐标代入抛物线解析式，得  ，解得 ∴抛物线的解析式为  ………4分（2）设点P的横坐标为m，作PE⊥AB于E 则  ……………………5分∵A（－4，0），C（0，－3），∠AOC＝90° ∴OA＝4，OC＝3，AC＝  ∴  ……………………………………………………6分∵PD∥y轴 ∴∠PDB＝∠ACO，∴  在Rt△PDE中，  ……8分∵  ， ，∴当 时，PE取最大值 ∴点P到直线AB的距离的最大值是  ……………………………………9分（3）存在，满足条件的点有三组…………………………………………10分 P1（  ， ），Q1（0， ）……………………………………11分P2（  ， ），Q2（0， ）………………………12分P3（  ， ），Q3（0， ）………………………13分 (责任编辑：admin) |