|
☆☆☆ 点击下载试题 ☆☆☆ 各位同学在查看时请点击全屏查看 2018年遵义中考数学冲刺试题 考生注意: 1.本卷为数学试题卷,全卷共4页,三大题25小题,满分150分.考试时间为120分钟. 2.一律在《答题卡》相应位置作答,在试题卷上答题视为无效. 3.可以使用科学计算器. 一、选择题(以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,请用2B铅笔在《答题卡》上填涂正确选项的字母框,每小题3分,共30分) 二、填空题(每小题4分,共20分) 1.-4的绝对值等于( ) (A) 4 (B) 2.将 (A) 3.从贵阳市招生考试管理中心获悉,2010年全市参加初中学业文化适应性考试总人数达51087人,这里的数字51087用科学记数法表示为( ) (A) 4. 在下面的四个几何体中,它们各自的左视图与主视图可能不相同的是( )  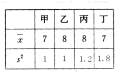 5. 四名运动员参加了射击预选赛,他们成绩的平均环数 (A)甲 (B) 乙 (C) 丙 (D) 丁 6.两个相似三角形的面积比为4︰9,则它们对应的相似比是( ) (A) 7. 要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( ) (A)调查全体女生 (B)调查全体男生 (C)调查九年级全体学生 (D)调查七、八、九年级各100名学生 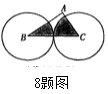 8. 8. 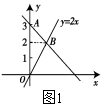 (A) (A)9.如图1,过A点的一次函数 (A) 10.我们常用的数是十进制数,而计算机程序处理数据使用的只有数码0和1的二进制数,这二者可以相互换算,如将二进制数1011换算成十进制数应为: 按此方式,则将十进制数7换算成二进制数应为( ) (A)101 (B) 110 (C)111 (D)1101 二、填空题(每小题4分,共20分) 11.若( )×(-2) = 1,则“( )”内应填的实数是 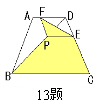 12. 在一个不透明的布袋中装有2个白球和 12. 在一个不透明的布袋中装有2个白球和13. 如图,等腰梯形ABCD中,AD=2,AB=4, 14.图象经过点(2,-5)的函数表达式为 (写出一个即可) . 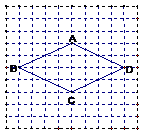 15.如图,正方形网格中,四边形ABCD是格点四边形(顶点都是格点),设网格小正方形的边长为1,则四边形ABCD能覆盖的网格小正方形的个数为 。 15.如图,正方形网格中,四边形ABCD是格点四边形(顶点都是格点),设网格小正方形的边长为1,则四边形ABCD能覆盖的网格小正方形的个数为 。三、解答题 16.(本题满分8分)先化简代数式 再从 17.(本小题满分10分)2009年秋季以来,我国西南地区遭受了严重的旱情,某校学生会自发组织了“保护水资源从我做起”的活动. 同学们采取问卷调查的方式,随机调查了本校150名同学家庭月人均用水量和节水措施情况.以下是根据调查结果做出的统计图的一部分。请根据以上信息解答下列问题: (1)补全图1和图2; 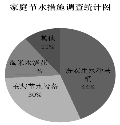 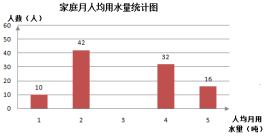 (2)如果全校学生家庭总人数为3000人,根据这150名同学家庭月人均用水量,估计全校学生家庭月用水总量多少吨? (2)如果全校学生家庭总人数为3000人,根据这150名同学家庭月人均用水量,估计全校学生家庭月用水总量多少吨?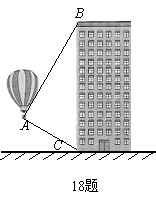 图1 图2 18.(本题满分10分)如图,热气球的探测器显示,从热气球 点A看一栋高楼顶部的仰角为 为 高? 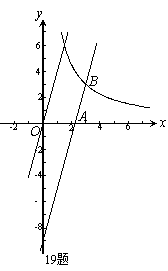 (结果精确到0.1 m,参考数据: (结果精确到0.1 m,参考数据:19.(本题满分10分)在平面几何中,我们学过两条直线平行的定义. 下面就两个一次函数的图象所确定的两知直线,给出它们平行的定义: 设一次函数 一次函数 若 如图,将直线 x轴交于点A( (1)求直线AB的解析式;(4分) (2)若点B的纵坐标为m,求双曲线解析式(用含m的代数式表示). 20. (本题满分10分) 某电脑公司现有A,B,C三种型号的电脑和D,E两种型号的打印机.某校要从其中选购一台电脑和一台打印机送给山区小学. (1) 写出所有选购方案(利用树状图或列表方法表示); (2) 已知A、D是甲厂生产的产品,B、C、E是乙厂生产的产品.如果(1)中各种选购方案被选中的可能性相同,那么甲厂生产的产品被选中的概率是多少?  21.(本题满分10分)如图,在Rt△ABC中,已知∠BCA=90º,∠BAC=30º, AB=6cm。把△ABC以点B为中心逆时针旋转,使点C旋转到AB边的延长线上得到 21.(本题满分10分)如图,在Rt△ABC中,已知∠BCA=90º,∠BAC=30º, AB=6cm。把△ABC以点B为中心逆时针旋转,使点C旋转到AB边的延长线上得到(1)作出 (2)用阴影表示旋转过程中边AC扫过的图形,  然后求出它的面积(结果用 然后求出它的面积(结果用22.(10分)如图,在△ABC中,D是BC边的中点,F、E分别是 AD及其延长线上的点,CF∥BE (1)求证:BE=CF;(4分) (2)连接BF、CE,如果△ABC中,AB=AC,那么四边形 BECF的形状一定是 . 并证明你的结论。(6分) 23.(本题满分10分)某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品,共50件。已知生产一件A种产品,需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品,需用甲种原料4千克、乙种原料10千克,可获利润1200元。 (1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;  (2)设生产A、B两种产品获总利润为 (2)设生产A、B两种产品获总利润为24.(本题满分10分)如图,⊙O的直径AB=4,C为圆周 上一点,AC=2,过点C作⊙O的 切线l,过点B作 l的垂线BD,垂足为D,BD与⊙O交于点 E. (1) 求∠AEC的度数; (4分) (2)求证:四边形OBEC是菱形.(6分) 25.(本题满分12分)某蔬菜基地种植的某种绿色蔬菜,根据今年的市场行情,预计从5月1日起的50天内,它的市场售价y1与上市时间x的关系可用图(a)的一条线段表示;它的种植成本y2与上市时间x的关系可用图(b)中的抛物线的一部分来表示. (1)求出图(a)中表示的市场售价y1与上市时间x的函数关系式.(3分) (2)求出图(b)中表示的种植成本y2与上市时间x的函数关系式.(3分) 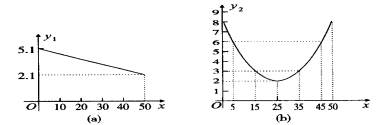 (3)假定市场售价减去种植成本为纯利润,问哪天上市的这种绿色蔬菜既不赔本也不赚钱?(市场售价和种植成本的单位:元/千克,时间单位:天)(6分) (3)假定市场售价减去种植成本为纯利润,问哪天上市的这种绿色蔬菜既不赔本也不赚钱?(市场售价和种植成本的单位:元/千克,时间单位:天)(6分)2018年遵义中考数学冲刺试题参考答案 一、选择题(每小题3分,共30分) 1~5. A B C D B 6~10. B D C C C 二、填空题(每小题4分,共20分) 11. 二、解答题: 16.(本题满分8分) 解:原式= = = 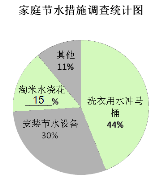 令x=0(只要 令x=0(只要17.(本小题10分)解:(1) 2分-----4分 (2) 全体学生家庭月人均用水量为 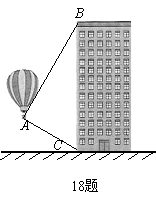 答:全校学生家庭月用水量约为 9040吨.--------------------------10分 答:全校学生家庭月用水量约为 9040吨.--------------------------10分18.(本小题10分) 解:如图8,过点 根据题意,可得 在Rt△ 得BD= AD×tan600 =60 在Rt△ 得CD= AD×tan300 =20 ∴.BC=CD+BD=60 答:这栋楼高约为138.4 m. 10分 19. (本小题10分) 解:(1)将直线 设直线AB的解析式为 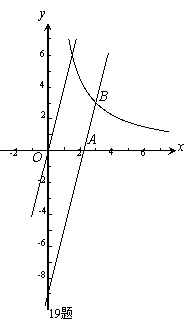 则 则解得 ∴直线AB的解析式为 (2)设点B的坐标为(xB,m), ∵直线AB经过点B, 5分 ∴ ∴B点的坐标为( ∵点B在双曲线 ∴ 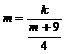 . ∴ . ∴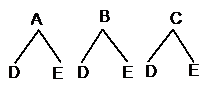 ∴双曲线解析式为: ∴双曲线解析式为: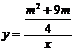 10分 10分20.(本小题10分)解:(1) 树状图如下: 甲品牌 乙品牌 有6种可能结果:(A,D),(A,E),(B,D),(B,E),(C,D),(C,E). 或列表如下:
5分 (2) 因为选中B型号电脑有2种方案,即(B,D)、(B,E),所以B型号电脑选中的概率是  21.(本小题10分) 21.(本小题10分)解: (1)如图 (2)AC扫过的图形如图中阴影部份. ∵在 ∴ 以B为圆心作弧交AB于D,据旋转性质可知,阴影面积 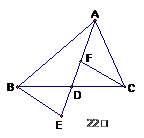 答:AC扫过的图形面积为 22.(本小题10分) (1)证明: (2) 23.(本小题10分) 解:(1)设需生产A种产品 ∵ ∴ ∴有三种生产方案:①生产A种产品30件,生产B种产品20件;②生产A种产品31件,生产B种产品19件;③生产A种产品32件,生产B种产品18件。 (2)由题意得; ∵ ∴当 答: 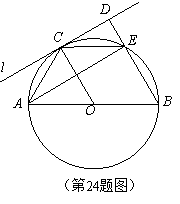 24.(本小题10分) 24.(本小题10分)(1)解:在△AOC中,AC=2, ∵ AO=OC=2, ∴ △AOC是等边三角形. 2分 ∴ ∠AOC=60°, ∴∠AEC=30°. 4分 (2)证明:∵OC⊥l,BD⊥l. ∴ OC∥BD. 5分 ∴ ∠ABD=∠AOC=60°. ∵ AB为⊙O的直径, ∴ △AEB为直角三角形,∠EAB=30°. 7分 ∴∠EAB=∠AEC. ∴ 四边形OBEC 为平行四边形. 9分 又∵ OB=OC=2. ∴ 四边形OBEC是菱形. 10分 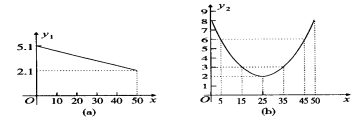 25. (本小题12分) 25. (本小题12分)(1)设 ∴ 解得: ∴ (2)又由题目已知条件可设 ∴ ∴ (3)第 依题意:y1-y2=0,即x2-44x+315=0,∴(x-9)(x-35)=0,解得:x1=9,x2=25. 所以从5月1日起的第9天或第35天出售的这种绿色蔬菜,既不赔本也不赚钱. (责任编辑:admin) |
