|
☆☆☆ 点击下载试题 ☆☆☆ 请点击全屏查看 2016辽阳市辽阳县中考数学一模试卷 一、选择题（每小题3分，共30分） 1．﹣  的绝对值是（ ）A．﹣2016 B． C．﹣ D．20162．下面的计算正确的是（ ） A．3x2•4x2=12x2 B．x3•x5=x15 C．x4÷x=x3 D．（x5）2=x7 3．太阳的温度很高，其表面温度大概有6 000℃，而太阳中心的温度达到了19 200 000℃，用科学记数法可将19 200 000表示为（ ） A．1.92×106 B．1.92×107 C．1.92×108 D．1.92×109 4．（2016辽阳数学）如图，已知BD∥AC，∠1=65°，∠A=40°，则∠2的大小是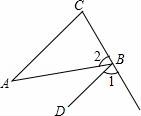（ ）  A．55° B．65° C．75° D．85° 5．一个几何体的三视图如图所示，那么这个几何体的侧面积是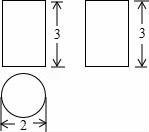（ ）  A．4π B．6π C．8π D．12π 6．（2016辽阳数学）如图，△ABC为等腰直角三角形，∠ACB=90°，将△ABC绕点 A逆时针旋转75°，得到△AB′C′，过点B′作B′D⊥CA，交CA的延长线于点D，若AC=6，则AD的长为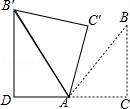（ ）  A．2 B．3 C．2  D．3 7．（2016辽阳数学）若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有不相等实数根，则k的取值范围是（ ） A．k＞  B．k≥ C．k＞且k≠1 D．k≥且k≠18．小明记录了某市连续10天的最高气温如表：
那么关于这10天的最高气温的说法正确的是（ ） A．中位数23.5 B．众数22 C．方差46 D．平均数24 9．商场举行摸奖促销活动，对于“抽到一等奖的概率为O.1”．下列说法正确的是（ ） A．抽10次奖必有一次抽到一等奖 B．抽一次不可能抽到一等奖 C．抽10次也可能没有抽到一等奖 D．抽了9次如果没有抽到一等奖，那么再抽一次肯定抽到一等奖 10．如图，已知点A（4，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与射线AC相交于点D．当△ODA是等边三角形时，这两个二次函数的最大值之和等于（ ）  A．  B． C．2 D． 二、（2016辽阳数学）填空题（每小题3分，共24分） 11．把多项式2a3﹣8a分解因式的结果是 ． 12．使  有意义的x的取值范围是 ．13．在一个不透明的口袋中，有四个完全相同的小球，把它们分别标号为1、2、3、4，随机地摸取一个小球记下标号后放回，再随机地摸取一个小球记下标号，则两次摸取的小球标号都是1的概率为 ． 14．如图，在矩形ABCD中，AB=2DA，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设DA=2，图中阴影部分的面积为 ．  15．（2016辽阳数学）在江岸区创建文明城区的活动中，有两段长度相等的彩色砖道铺设任务，分别交给甲、乙两个施工队同时进行施工．如图是反映所铺设彩色砖道的长度y（米）与施工时间x（时）之间关系的部分图象．如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加到12米/时，结果两队同时完成了任务，则甲队从开始施工到完工所铺设的彩色道砖的长度为 米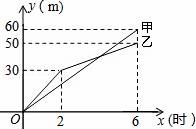．  16．如图，BC是⊙O弦，D是BC上一点，DO交⊙O于点A，连接AB、OC，若∠A=20°，∠C=30°，则∠AOC的度数为 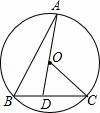．  17．（2016辽阳数学）如图，在平面直角坐标系中，Rt△ABO的顶点O与原点重合，顶点B在x轴上，∠ABO=90°，OA与反比例函数y= 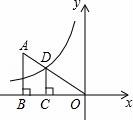 的图象交于点D，且OD=2AD，过点D作x轴的垂线交x轴于点C．若S四边形ABCD=10，则k的值为 ． 18．如图，n+1个边长为2的等边三角形有一条边在同一直线上，设△B2D1C1的面积为S1，△B3D2C2的面积为S2，…，△Bn+1DnCn的面积为Sn，则S2= ；Sn= ．（用含n的式子表示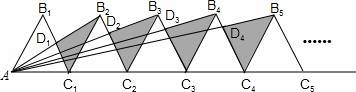）  三、（2016辽阳数学）解答题（第19题10分，第20题12分，共22分） 19．先化简，后求值：  ，其中x=3．20．为了贯彻“减负增效”精神，掌握2014～2015学年度九年级600名学生每天的自主学习情况，某校学生会随机抽查了2014～2015学年度九年级的部分学生，并调查他们每天自主学习的时间．根据调查结果，制作了两幅不完整的统计图（图1，图2），请根据统计图中的信息回答下列问题： （1）本次调查的学生人数是 人； （2）图2中α是 度，并将图1条形统计图补充完整； （3）请估算该校2014～2015学年度九年级学生自主学习时间不少于1.5小时有 人； （4）老师想从学习效果较好的4位同学（分别记为A，B，C，D，其中A为小亮）随机选择两位进行学习经验交流，用列表法或树状图的方法求出选中小亮A的概率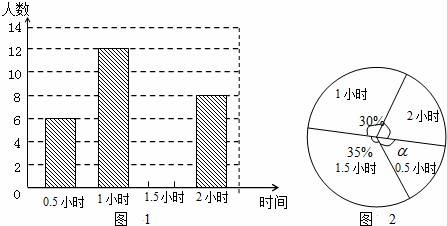．  四、（2016辽阳数学）解答题（每题12分，共24分） 21．如图，己知点A（1，  ）在反比例函数y= （x＞0）的图象上，连接OA，将线段OA绕点D顺时针方向旋转30°，得到线段OB．（1）求反比例函数的解析式； （2）判断点B是否在反比例函数图象上，并说明理由； （3）设直线AB的解析式为y=ax+b，请直接写出不等式ax+b﹣ 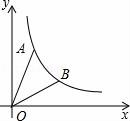＜0的解集． 22．某超市用3000元购进某种干果，由于销售状况良好，超市又用9000元第二次购进该干果，但第二次的进价比第一次的提高了20%，第二次购进干果数量是第一次的2倍还多300千克． （1）求该干果的第一次进价是每千克多少元？ （2）百姓超市按每千克9元的价格出售，当大部分干果售出后，余下的按售价的8折售完，若两次销售这种干果的利润不少于5820元，则最多余下多少千克干果按售价的8折销售． 五、（2016辽阳数学）解答题 23．如图，某风景区的湖心岛有一凉亭A，其正东方向有一棵大树B，小明想测量A、B之间的距离，他从湖边的C处测得A在北偏西45°方向上，测得B在北偏东32°方向上，且量得B、C之间的距离为100米，根据上述测量结果，请你帮小明计算A、B之间的距离是多少？（精确到1米，参考数据：sin32°=0.5299，cos32°=0.8480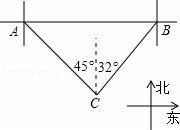）  六（2016辽阳数学）、解答题 24．如图，AB为⊙O的直径，P是BA延长线上一点，PC切⊙O于点C，CG是⊙O的弦，CG⊥AB，垂足为D． （1）求证：∠PCA=∠ABC； （2）过点A作AE∥PC，交⊙O于点E，交CD于点F，连接BE．若sin∠P= 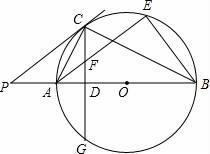 ，CF=5，求BE的长． 七、解答题 25．已知：正方形ABCD的边长为4，点E为BC的中点，点P为AB上一动点，沿PE翻折△BPE得到△FPE，直线PF交CD边于点Q，交直线AD于点G，联接EQ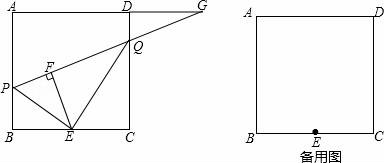．  （1）如图，当BP=1.5时，求CQ的长； （2）如图，当点G在射线AD上时，BP=x，DG=y，求y关于x的函数关系式，并写出x的取值范围； （3）延长EF交直线AD于点H，若△CQE与△FHG相似，求BP的长． 八（2016辽阳数学）解答题 26．在平面直角坐标系xOy中，已知抛物线y=﹣  +c与x轴交于A、B两点（点A在点B的左侧），交y轴的正半轴于点C，其顶点为M，MH⊥x轴于点H，MA交y轴于点N，sin∠MOH= ．（1）求此抛物线的函数表达式； （2）过H的直线与y轴相交于点P，过O，M两点作直线PH的垂线，垂足分别为E，F，若  = 时，求点P的坐标；（3）将（1）中的抛物线沿y轴折叠，使点A落在点D处，连接MD，Q为（1）中的抛物线上的一动点，直线NQ交x轴于点G，当Q点在抛物线上运动时，是否存在点Q，使△ANG与△ADM相似？若存在，求出所有符合条件的直线QG的解析式；若不存在，请说明理由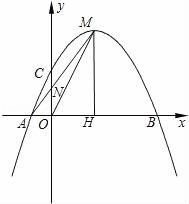．  2016辽阳数学参考答案与试题解析 一、选择题（每小题3分，共30分） 1．﹣  的绝对值是（ ）A．﹣2016 B． C．﹣ D．2016【考点】绝对值． 【分析】根据相反数的意义，求解即可．注意正数的绝对值是本身，0的绝对值为0，负数的绝对值是其相反数． 【解答】解：∵﹣ 的绝对值等于其相反数，∴﹣ 的绝对值是．故选B 2．（2016辽阳数学）下面的计算正确的是（ ） A．3x2•4x2=12x2 B．x3•x5=x15 C．x4÷x=x3 D．（x5）2=x7 【考点】同底数幂的除法；同底数幂的乘法；幂的乘方与积的乘方；单项式乘单项式． 【分析】根据单项式的乘法、同底数幂的乘法和除法、幂的乘方等知识点进行判断． 【解答】解：A、3x2•4x2=12x4，故本选项错误； B、x3•x5=x8，故本选项错误； C、正确； D、（x5）2=x10，故本选项错误． 故选C． 3．太阳的温度很高，其表面温度大概有6 000℃，而太阳中心的温度达到了19 200 000℃，用科学记数法可将19 200 000表示为（ ） A．1.92×106 B．1.92×107 C．1.92×108 D．1.92×109 【考点】科学记数法—表示较大的数． 【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数． 【解答】解：将19 200 000用科学记数法表示为：1.92×107． 故选：B． 4．（2016辽阳数学）如图，已知BD∥AC，∠1=65°，∠A=40°，则∠2的大小是（ ） A．55° B．65° C．75° D．85° 【考点】平行线的性质． 【分析】先根据平行线的性质求出∠C，再根据三角形内角和定理求出∠2的大小即可． 【解答】解：∵BD∥AC，∠1=65°， ∴∠C=∠1=65°， ∵∠A=40°， ∴∠2=180°﹣∠A﹣∠C=75°， 故选C． 5．一个几何体的三视图如图所示，那么这个几何体的侧面积是（ ）  A．4π B．6π C．8π D．12π 【考点】（2016辽阳数学）由三视图判断几何体． 【分析】根据三视图正视图以及左视图都为矩形，底面是圆形，则可想象出这是一个圆柱体．侧面积=底面周长×高． 【解答】解：∵圆柱的直径为2，高为3， ∴侧面积为2× ×2×3π=6π．故选B． 6．如图，△ABC为等腰直角三角形，∠ACB=90°，将△ABC绕点 A逆时针旋转75°，得到△AB′C′，过点B′作B′D⊥CA，交CA的延长线于点D，若AC=6，则AD的长为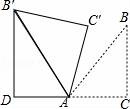（ ）  A．2 B．3 C．2 D．3 【考点】旋转的性质． 【分析】在直角△ABC中利用勾股定理即可求得AB的长，则AB′的长即可求得，然后根据旋转角的定义利用角的和差求得∠B′AD的度数，在直角△B′AD中利用三角函数即可求解． 【解答】（2016辽阳数学）解：在直角△ABC中，AB=  = =6 ，则AB'=AB=6 ．在直角△B'AD中，∠B′AD=180°﹣∠BAC﹣∠BAB′=180°﹣45°﹣75°=60°． 则AD=AB′•cos∠B′AD=6 × =3．故选D． 7．若关于x的一元二次方程（k﹣1）x2+2x﹣2=0有不相等实数根，则k的取值范围是（ ） A．k＞ B．k≥ C．k＞且k≠1 D．k≥且k≠1【考点】根的判别式；一元二次方程的定义． 【分析】根据判别式的意义得到△=22﹣4（k﹣1）×（﹣2）＞0，然后解不等式即可． 【解答】解：∵关于x的一元二次方程（k﹣1）x2+2x﹣2=0有不相等实数根， ∴△=22﹣4（k﹣1）×（﹣2）＞0， 解得k＞  ；且k﹣1≠0，即k≠1．故选：C． 8．（2016辽阳数学）小明记录了某市连续10天的最高气温如表：
那么关于这10天的最高气温的说法正确的是（ ） A．中位数23.5 B．众数22 C．方差46 D．平均数24 【考点】方差；加权平均数；中位数；众数． 【分析】利用方差的计算公式、加权平均数的计算公式、中位数及众数的定义分别求解后即可确定正确的选项． 【解答】解：A、排序后位于中间位置的两数为25，25，故中位数为25，故错误； B、数据26出现了4次，最多，故众数为26，故错误； 平均数为  （20+22×3+25×2+26×4）=24，方差为 [（20﹣24）2+3×（22﹣24）2+2×（25﹣24）2+4×（26﹣24）2]=44，故错误；故D正确， 故选D． 9．商场举行摸奖促销活动，对于“抽到一等奖的概率为O.1”．下列说法正确的是（ ） A．抽10次奖必有一次抽到一等奖 B．抽一次不可能抽到一等奖 C．抽10次也可能没有抽到一等奖 D．抽了9次如果没有抽到一等奖，那么再抽一次肯定抽到一等奖 【考点】（2016辽阳数学）概率的意义． 【分析】根据概率是频率（多个）的波动稳定值，是对事件发生可能性大小的量的表现进行解答即可． 【解答】解：根据概率的意义可得“抽到一等奖的概率为O.1”就是说抽10次可能抽到一等奖，也可能没有抽到一等奖， 故选：C． 10．如图，已知点A（4，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与射线AC相交于点D．当△ODA是等边三角形时，这两个二次函数的最大值之和等于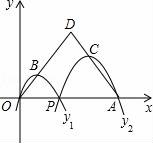（ ）  A．  B． C．2 D． 【考点】（2016辽阳数学）二次函数的最值；等边三角形的性质． 【分析】连接PB、PC，根据二次函数的对称性可知OB=PB，PC=AC，从而判断出△POB和△ACP是等边三角形，再根据等边三角形的性质求解即可． 【解答】解：如图，连接PB、PC， 由二次函数的性质，OB=PB，PC=AC， ∵△ODA是等边三角形， ∴∠AOD=∠OAD=60°， ∴△POB和△ACP是等边三角形， ∵A（4，0）， ∴OA=4， ∴点B、C的纵坐标之和为4×  =2，即两个二次函数的最大值之和等于2  ．故选C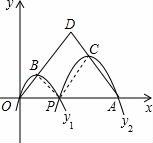．  二、（2016辽阳数学）填空题（每小题3分，共24分） 11．把多项式2a3﹣8a分解因式的结果是 2a（a+2）（a﹣2） ． 【考点】提公因式法与公式法的综合运用． 【分析】首先提取公因式进而利用平方差公式法分解因式得出即可． 【解答】解：2a3﹣8a=2a（a2﹣4）=2a（a+2）（a﹣2）． 故答案为：2a（a+2）（a﹣2）． 12．使  有意义的x的取值范围是 x≥2 ．【考点】二次根式有意义的条件． 【分析】当被开方数x﹣2为非负数时，二次根式才有意义，列不等式求解． 【解答】解：根据二次根式的意义，得 x﹣2≥0，解得x≥2． 13．（2016辽阳数学）在一个不透明的口袋中，有四个完全相同的小球，把它们分别标号为1、2、3、4，随机地摸取一个小球记下标号后放回，再随机地摸取一个小球记下标号，则两次摸取的小球标号都是1的概率为  ．【考点】列表法与树状图法． 【分析】列表得出所有等可能的情况数，找出两次摸取的小球标号都是1的情况数，即可求出所求的概率． 【解答】解：列表如下：
所有等可能的情况有16种，其中两次摸取的小球标号都是1的情况有1种， 则P= ．故答案为： 14．如图，在矩形ABCD中，AB=2DA，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设DA=2，图中阴影部分的面积为 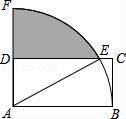 π﹣2 ． 【考点】矩形的性质；扇形面积的计算． 【分析】（2016辽阳数学）根据直角三角形30°角所对的直角边等于斜边的一半可得∠AED=30°，然后求出DE，再根据阴影部分的面积=S扇形AEF﹣S△ADE列式计算即可得解． 【解答】解：∵AB=2DA，AB=AE（扇形的半径）， ∴AE=2DA=2×2=4， ∴∠AED=30°， ∴∠DAE=90°﹣30°=60°， DE=  = =2，∴阴影部分的面积=S扇形AEF﹣S△ADE， =  ﹣×2×2，=  π﹣2．故答案为： π﹣2 ．15．在江岸区创建文明城区的活动中，有两段长度相等的彩色砖道铺设任务，分别交给甲、乙两个施工队同时进行施工．如图是反映所铺设彩色砖道的长度y（米）与施工时间x（时）之间关系的部分图象．如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加到12米/时，结果两队同时完成了任务，则甲队从开始施工到完工所铺设的彩色道砖的长度为 110 米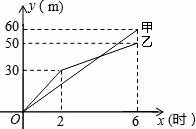．  【考点】（2016辽阳数学）一次函数的应用． 【分析】（1）设函数关系是为y=kx+b，然后利用待定系数法求解即可； （2）先求出甲队的速度，然后设甲队从开始到完工所铺设彩色砖道的长度为z米，再根据6小时后两队所用的时间相等列方程求解即可． 【解答】解：（1）设乙队在2≤x≤6的时段内y与x之间的函数关系式为y=kx+b， 由图可知，函数图象过点（2，30），（6，50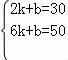），  ，解得  ．∴y=5x+20； （2）由图可知，甲队速度是：60÷6=10（米/时）， 设甲队从开始到完工所铺设彩色道砖的长度为z米， 依题意得  ，解得z=110． 答：甲队从开始到完工所铺设彩色道砖的长度为110米． 16．如图，BC是⊙O弦，D是BC上一点，DO交⊙O于点A，连接AB、OC，若∠A=20°，∠C=30°，则∠AOC的度数为 100° 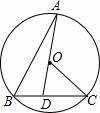．  【考点】（2016辽阳数学）圆周角定理． 【分析】设∠AOC=x°，根据圆周角定理得到∠B的度数，根据三角形的外角的性质列出方程，解方程得到答案． 【解答】解：设∠AOC=x°，则∠B=  x°，∵∠AOC=∠ODC+∠C，∠ODC=∠B+∠A， ∴x=20°+30°+ x，解得x=100°． 故答案为：100°． 17．如图，在平面直角坐标系中，Rt△ABO的顶点O与原点重合，顶点B在x轴上，∠ABO=90°，OA与反比例函数y= 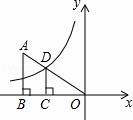 的图象交于点D，且OD=2AD，过点D作x轴的垂线交x轴于点C．若S四边形ABCD=10，则k的值为 ﹣16 ． 【考点】相似三角形的判定与性质；反比例函数系数k的几何意义． 【分析】（2016辽阳数学）证△DCO∽△ABO，推出  = = = ，求出 =（）2= ，求出S△ODC=8，根据三角形面积公式得出OC×CD=8，求出OC×CD=16即可．【解答】解：∵OD=2AD， ∴ =，∵∠ABO=90°，DC⊥OB， ∴AB∥DC， ∴△DCO∽△ABO， ∴ ===，∴ =（）2=，∵S四边形ABCD=10， ∴S△ODC=8， ∴  OC×CD=8，OC×CD=16， ∵双曲线在第二象限， ∴k=﹣16， 故答案为：﹣16． 18．（2016辽阳数学）如图，n+1个边长为2的等边三角形有一条边在同一直线上，设△B2D1C1的面积为S1，△B3D2C2的面积为S2，…，△Bn+1DnCn的面积为Sn，则S2= 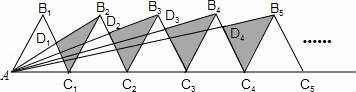 ；Sn=  ．（用含n的式子表示） 【考点】相似三角形的判定与性质；等边三角形的性质． 【分析】由三角形的相似性可求得S2、S3、S4的值，则Sn的值也可用含n的式子表示出来． 【解答】（2016辽阳数学）解：由于各三角形为等边三角形，且各边长为2，过各三角形的顶点B1、B2、B3…向对边作垂线，垂足为M1、M2、M3， ∵△AB1C1是等边三角形， ∴AD1=AC1•sin60°=2× =，∵△B1C1B2也是等边三角形， ∴C1B1是∠AC1B2的角平分线， ∴AD1=B2D1= ，故S1=S△B2C1A﹣S△AC1D1= ×2×﹣×2×=；S2=S△B3C2A﹣S△AC2D2= ×4×﹣×4× =2﹣ =；作AB∥B1C1，使AB=AB1，连接BB1，则B2，B3，…Bn在一条直线上． ∵Bn Cn∥AB， ∴  = = ，∴BnDn= •AB= ，则DnCn=2﹣BnDn=2﹣ = ．△BnCnBn+1是边长是2的等边三角形，因而面积是： ．△Bn+1DnCn面积为Sn=  •= •= ．即第n个图形的面积Sn= 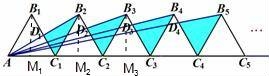． 三、解答题（第19题10分，第20题12分，共22分） 19．先化简，后求值：  ，其中x=3．【考点】分式的化简求值． 【分析】首先将括号里面通分，能分解因式的分解因式，进而化简后求值得出． 【解答】解： ，=（  + ）× =  × =  ，当x=3时，原式=  = ．20．（2016辽阳数学）为了贯彻“减负增效”精神，掌握2014～2015学年度九年级600名学生每天的自主学习情况，某校学生会随机抽查了2014～2015学年度九年级的部分学生，并调查他们每天自主学习的时间．根据调查结果，制作了两幅不完整的统计图（图1，图2），请根据统计图中的信息回答下列问题： （1）本次调查的学生人数是 40 人； （2）图2中α是 54 度，并将图1条形统计图补充完整； （3）请估算该校2014～2015学年度九年级学生自主学习时间不少于1.5小时有 330 人； （4）老师想从学习效果较好的4位同学（分别记为A，B，C，D，其中A为小亮）随机选择两位进行学习经验交流，用列表法或树状图的方法求出选中小亮A的概率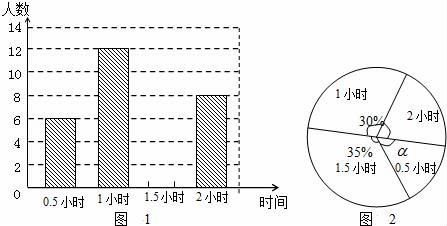．  【考点】列表法与树状图法；用样本估计总体；扇形统计图；条形统计图． 【分析】（2016辽阳数学）（1）由自主学习的时间是1小时的有12人，占30%，即可求得本次调查的学生人数； （2）由  ×360°=54°，40×35%=14；即可求得答案；（3）首先求得这40名学生自主学习时间不少于1.5小时的百分比，然后可求得该校九年级学生自主学习时间不少于1.5小时的人数； （4）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与选中小亮A的情况，再利用概率公式求解即可求得答案． 【解答】解：（1）∵自主学习的时间是1小时的有12人，占30%， ∴12÷30%=40， 故答案为：40； （2） ×360°=54°，40×35%=14；补充图形如图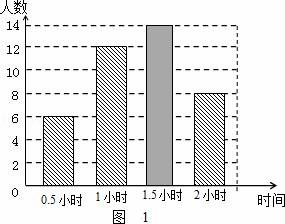：  ，故答案为：54； （3）600×  =330，故答案为：330； （4）画树状图得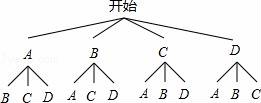：  ∵共有12种等可能的结果，选中小亮A的有6种， ∴P（A）=  =．四、（2016辽阳数学）解答题（每题12分，共24分） 21．如图，己知点A（1，  ）在反比例函数y= （x＞0）的图象上，连接OA，将线段OA绕点D顺时针方向旋转30°，得到线段OB．（1）求反比例函数的解析式； （2）判断点B是否在反比例函数图象上，并说明理由； （3）设直线AB的解析式为y=ax+b，请直接写出不等式ax+b﹣ 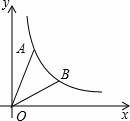＜0的解集． 【考点】反比例函数与一次函数的交点问题． 【分析】（1）根据反比例函数图象上点的坐标特征可计算出k= ，于是得到反比例函数解析式为y= ；（2）作AE⊥y轴于E，BF⊥x轴于F，如图，在Rt△OAE中根据正切定义得到tan∠AOE=  ，则∠AOE=30°，所以OA=2AE=2，再根据旋转的性质得∠AOB=30°，OB=OA=2，于是可计算出∠BOF=30°，接着在Rt△BOF中，利用含30度的直角三角形三边的关系得BF=OB=1，OF= BF=，则B（，1），然后根据反比例函数图象上点的坐标特征判断点B（，1）是否在反比例函数y= 的图象上；（2）观察函数图象，写出反比例函数图象在直线AB上方所对应的自变量的范围即可． 【解答】（2016辽阳数学）解：（1）∵点A（1， ）在反比例函数y=（x＞0）的图象上，∴k=1× =，∴反比例函数解析式为y= ；（2）点B在反比例函数图象上．理由如下： 作AE⊥y轴于E，BF⊥x轴于F，如图， 在Rt△OAE中，∵AE=1，OE= ，∴tan∠AOE=  = ，∴∠AOE=30°，OA=2AE=2， ∵线段OA绕点O顺时针方向旋转30°，得到线段OB， ∴∠AOB=30°，OB=OA=2， ∴∠BOF=30°， 在Rt△BOF中，BF= OB=1，OF= BF=，∴B（ ，1），∵当x= 时，y= =1，∴点B（ ，1）在反比例函数y=的图象上；（2）0＜x＜1或x＞ ． 22．（2016辽阳数学）某超市用3000元购进某种干果，由于销售状况良好，超市又用9000元第二次购进该干果，但第二次的进价比第一次的提高了20%，第二次购进干果数量是第一次的2倍还多300千克． （1）求该干果的第一次进价是每千克多少元？ （2）百姓超市按每千克9元的价格出售，当大部分干果售出后，余下的按售价的8折售完，若两次销售这种干果的利润不少于5820元，则最多余下多少千克干果按售价的8折销售． 【考点】分式方程的应用；一元一次不等式的应用． 【分析】（1）设该种干果的第一次进价是每千克x元，则第二次进价是每千克（1+20%）x元．根据第二次购进干果数量是第一次的2倍还多300千克，列出方程，解方程即可求解． （2）根据利润=售价﹣进价列出不等式并解答． 【解答】解：（1）设该种干果的第一次进价是每千克x元，则第二次进价是每千克（1+20%）x元， 由题意，得  =2× +300，解得x=5， 经检验x=5是方程的解． 答：该种干果的第一次进价是每千克5元． （2）设当大部分干果售出后，余下a千克按售价的8折售完， 由题意得：[  + ﹣a]×9+9×80%a﹣≥5820，解得a≤600． 答：当大部分干果售出后，余下的按售价的8折售完，若两次销售这种干果的利润不少于5820元，则最多余下600千克干果按售价的8折销售． 五、（2016辽阳数学）解答题 23．如图，某风景区的湖心岛有一凉亭A，其正东方向有一棵大树B，小明想测量A、B之间的距离，他从湖边的C处测得A在北偏西45°方向上，测得B在北偏东32°方向上，且量得B、C之间的距离为100米，根据上述测量结果，请你帮小明计算A、B之间的距离是多少？（精确到1米，参考数据：sin32°=0.5299，cos32°=0.8480）  【考点】解直角三角形的应用-方向角问题． 【分析】本题可通过构建直角三角形来解答，过点C作AB的垂线交AB于D，CD是直角三角形ACD和CBD的公共直角边，要先求出CD的值然后再求AD，BD的值，进而得出AB的长． 【解答】（2016辽阳数学）解：过点C作AB的垂线交AB于D， ∵B点在A点的正东方向上， ∴∠ACD=45°，∠DCB=32°， 在Rt△BCD中，BC=100， ∴DB=BCsin32°≈1000.5299=52.99（米）， CD=BCcos32°≈1000.8480=84.80（米）， 在Rt△ACD中，AD=CD， ∴AB=AD+DB≈84.80+52.99=137.79（米）≈138（米）．  六、（2016辽阳数学）解答题 24．如图，AB为⊙O的直径，P是BA延长线上一点，PC切⊙O于点C，CG是⊙O的弦，CG⊥AB，垂足为D． （1）求证：∠PCA=∠ABC； （2）过点A作AE∥PC，交⊙O于点E，交CD于点F，连接BE．若sin∠P= ，CF=5，求BE的长．【考点】切线的性质；勾股定理；解直角三角形． 【分析】（1）连接OC，由PC切⊙O于点C，得到OC⊥PC，于是得到∠PCA+∠OCA=90°，由AB为⊙O的直径，得到∠ABC+∠OAC=90°，由于OC=OA，证得∠OCA=∠OAC，于是得到结论； （2）由AE∥PC，得到∠PCA=∠CAF根据垂径定理得到  ，于是得到∠ACF=∠ABC，由于∠PCA=∠ABC，推出∠ACF=∠CAF，根据等腰三角形的性质得到CF=AF，在Rt△AFD中，AF=5，sin∠FAD= ，求得FD=3，AD=4，CD=8，在Rt△OCD中，设OC=r，根据勾股定理得到方程r2=（r﹣4）2+82，解得r=10，得到AB=2r=20，由于AB为⊙O的直径，得到∠AEB=90°，在Rt△ABE中，由sin∠EAD=，得到 于是求得结论．【解答】（2016辽阳数学）（1）证明：连接OC， ∵PC切⊙O于点C， ∴OC⊥PC， ∴∠PCO=90°， ∴∠PCA+∠OCA=90°， ∵AB为⊙O的直径， ∴∠ACB=90°， ∴∠ABC+∠OAC=90°， ∵OC=OA， ∴∠OCA=∠OAC， ∴∠PCA=∠ABC； （2）解：∵AE∥PC， ∴∠PCA=∠CAF， ∵AB⊥CG， ∴ ，∴∠ACF=∠ABC， ∵∠PCA=∠ABC， ∴∠ACF=∠CAF， ∴CF=AF， ∵CF=5， ∴AF=5， ∵AE∥PC， ∴∠FAD=∠P， ∵sin∠P= ，∴sin∠FAD= ，在Rt△AFD中，AF=5，sin∠FAD= ，∴FD=3，AD=4，∴CD=8， 在Rt△OCD中，设OC=r， ∴r2=（r﹣4）2+82， ∴r=10， ∴AB=2r=20， ∵AB为⊙O的直径， ∴∠AEB=90°，在Rt△ABE中， ∵sin∠EAD=  ，∴ ，∵AB=20， ∴BE=12．  七、（2016辽阳数学）解答题 25．已知：正方形ABCD的边长为4，点E为BC的中点，点P为AB上一动点，沿PE翻折△BPE得到△FPE，直线PF交CD边于点Q，交直线AD于点G，联接EQ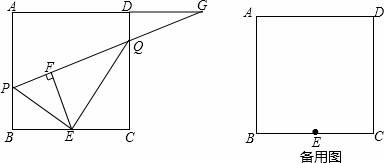．  （1）如图，当BP=1.5时，求CQ的长； （2）如图，当点G在射线AD上时，BP=x，DG=y，求y关于x的函数关系式，并写出x的取值范围； （3）延长EF交直线AD于点H，若△CQE与△FHG相似，求BP的长． 【考点】相似形综合题． 【分析】（1）首先确定∠PEQ=90°，即PE⊥EQ，然后利用△PBE∽△ECQ，列出比例式求出CD的长度； （2）根据△PBE∽△ECQ，求出DQ的表达式；由QD∥AP，列出比例式求解； （3）本问分两种情形，需要分类讨论，避免漏解． 【解答】（2016辽阳数学）解：（1）由翻折性质，可知PE为∠BPQ的角平分线，且BE=FE． ∵点E为BC中点， ∴EC=EB=EF， ∴QE为∠CQP的角平分线． ∵AB∥CD， ∴∠BPQ+∠CQP=180°，即2∠EPQ+2∠EQP=180°， ∴∠EPQ+∠EQP=90°， ∴∠PEQ=90°，即PE⊥EQ． 易证△PBE∽△ECQ， ∴  ，即 ，解得：CQ=  ．（2）由（1）知△PBE∽△ECQ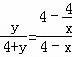， ∴  ，即 ，∴CQ=  ，∴DQ=4﹣．∵QD∥AP，∴  ，又AP=4﹣x，AG=4+y，∴  ，∴y=  （1＜x＜2）．（3）（2016辽阳数学）由题意知：∠C=90°=∠GFH． ①当点G在线段AD的延长线上时，如答图1所示． 由题意知：∠G=∠CQE ∵∠CQE=∠FQE， ∴∠DQG=∠FQC=2∠CQE=2∠G． ∵∠DQG+∠G=90°， ∴∠G=30°， ∴∠BEP=∠CQE=∠G=30°， ∴BP=BE•tan30°= 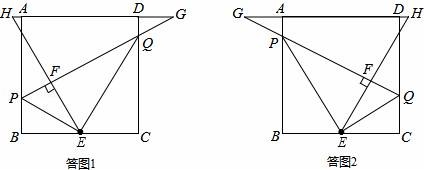 ； ②当点G在线段DA的延长线上时，如答图2所示． 由题意知：∠FHG=∠CQE． 同理可得：∠G=30°， ∴∠BPE=∠G=30°， ∴∠BEP=60°， ∴BP=BE•tan60°=  ．综上所述，BP的长为  或．八、（2016辽阳数学）解答题 26．在平面直角坐标系xOy中，已知抛物线y=﹣ +c与x轴交于A、B两点（点A在点B的左侧），交y轴的正半轴于点C，其顶点为M，MH⊥x轴于点H，MA交y轴于点N，sin∠MOH=．（1）求此抛物线的函数表达式； （2）过H的直线与y轴相交于点P，过O，M两点作直线PH的垂线，垂足分别为E，F，若 =时，求点P的坐标；（3）将（1）中的抛物线沿y轴折叠，使点A落在点D处，连接MD，Q为（1）中的抛物线上的一动点，直线NQ交x轴于点G，当Q点在抛物线上运动时，是否存在点Q，使△ANG与△ADM相似？若存在，求出所有符合条件的直线QG的解析式；若不存在，请说明理由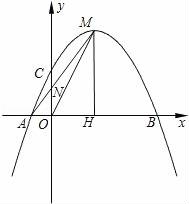．  【考点】二次函数综合题；勾股定理；相似三角形的判定与性质． 【分析】（2016辽阳数学）（1）由抛物线y=﹣  +c与x轴交于A、B两点（点A在点B的左侧），交y轴的正半轴于点C，其顶点为M，MH⊥x轴于点H，MA交y轴于点N，sin∠MOH= ，求出c的值，进而求出抛物线方程；（2）如图1，由OE⊥PH，MF⊥PH，MH⊥OH，可证△OEH∽△HFM，可知HE，HF的比例关系，求出P点坐标； （3）首先求出D点坐标，写出直线MD的表达式，由两直线平行，两三角形相似，可得NG∥MD，直线QG解析式． 【解答】解：（1）∵M为抛物线y=﹣ +c的顶点，∴M（2，c）． ∴OH=2，MH=|c|． ∵a＜0，且抛物线与x轴有交点， ∴c＞0， ∴MH=c， ∵sin∠MOH= ，∴  =．∴OM=  c，∵OM2=OH2+MH2， ∴MH=c=4， ∴M（2，4）， ∴抛物线的函数表达式为：y=﹣ +4．（2）如图1，∵OE⊥PH，MF⊥PH，MH⊥OH， ∴∠EHO=∠FMH，∠OEH=∠HFM． ∴△OEH∽△HFM， ∴  = =，∵ =，∴MF=HF， ∴∠OHP=∠FHM=45°， ∴OP=OH=2， ∴P（0，2）． （2016辽阳数学）如图2，同理可得，P（0，﹣2）．  （3）∵A（﹣1，0）， ∴D（1，0）， ∵M（2，4），D（1，0）， ∴直线MD解析式：y=4x﹣4， ∵ON∥MH，∴△AON∽△AHM， ∴  = = = ，∴AN=  ，ON= ，N（0，）．如图3，若△ANG∽△AMD，可得NG∥MD， ∴直线QG解析式：y=4x+ ，如图4，若△ANG∽△ADM，可得  = ∴AG=  ，∴G（  ，0），∴QG：y=﹣  x+ ，综上所述，符合条件的所有直线QG的解析式为：y=4x+ 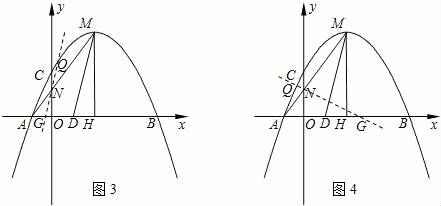或y=﹣x+． 第1页（共1页） (责任编辑：admin) |