|
☆☆☆ 点击下载试题 ☆☆☆ 此试题可能存在乱码情况,在查看时请点击右上角全屏查看 2018年株洲中考数学模拟试题 一、选择题:(本题24分) 1、下列各数中,比-1小的数是( ) A.0 B.-2 C. D.1 2、下列运算正确是( ) A.-(a-1)=-a-1 B.(a-b)2=a2-b2 C.=a D. a2•a3=a5 3、下列因式分解正确的是( ) A.x3﹣x=x(x2-1) B.x2+3x+2=x(x+3)+2 C.x2-y2=(x-y)2 D.x2+2x+1=(x+1)2 4、如图,一个小立方块所搭的几何体,从不同的方向看所得到的平面图形中(小正方形中的数字表示在该位置的小立方块的个数),不正确的是( ) 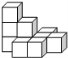 A. A.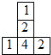 B. B.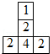 C. C.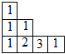 D. D.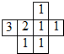 5、下列命题正确的个数是( )个. ①用四舍五入法按要求对0.05049分别取近似值为0.050(精确到0.001);②若代数式有意义,则x的取值范围是x≤-且x≠-2;③数据1、2、3、4的中位数是2.5 ;④月球距离地球表面约为384000000米,将这个距离用科学记数法(保留两个有效数字)表示为3.8×108米. A.1 B.2 C.3 D.4 6、如图1,在Rt△ABC中,AB=AC,AD⊥BC,垂足为D.E、F分别是CD、AD上的点,且CE=AF.如果∠AED=62°,那么∠DBF=( ) A.62° B.38° C.28° D.26° 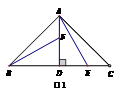 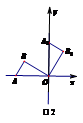 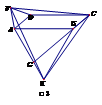 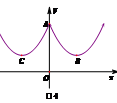 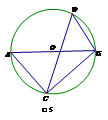 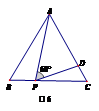 7、 如图2,将放置于直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A1OB1.已知∠AOB=30°,∠B=90°,AB=1,则B1点的坐标为( ) . A.(,) B.(,) C.(,) D (,) 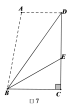 8、如图3,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( ) 8、如图3,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )A.只有①② B.只有①②③ C.只有③④ D.①②③④ 二、填空题:(本题24分) 9、已知 = = ,则 的值为 . 10、已知 11、如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为 . 12、如图5,AB是⊙O的直径,C,D两点在⊙O上,若∠BCD=40°,则∠ABD的度数为 . 13、将直径为16cm的圆形铁皮,做成四个相同圆锥容器的侧面(不浪费材料,不计接缝处的材料损耗),那么每个圆锥容器的高为 . 14、如图6,等边三角形ABC的边长为3,点P为BC边上一点,且BP=1,点D为AC边上一点,若∠APD=60°,则CD的长为 . 15、如图7,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点E处,若∠EBC=20°,则∠EBD的度数为 . 16、函数 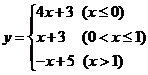 的最大值为 . 的最大值为 .三、解答题:(本题72分) 17、(本题满分6分)解不等式组 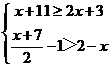 . .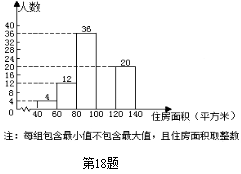 18、(本题满分6分)2012年北京春季房地产展示交易会期间,某公司对参加本次房交会的消费者的年收入和打算购买住房面积这两项内容进行了随机调查,共发放100份问卷,并全部收回.统计相关数据后,制成了如下的统计表和统计图: 消费者打算购买住房面积统计图 18、(本题满分6分)2012年北京春季房地产展示交易会期间,某公司对参加本次房交会的消费者的年收入和打算购买住房面积这两项内容进行了随机调查,共发放100份问卷,并全部收回.统计相关数据后,制成了如下的统计表和统计图: 消费者打算购买住房面积统计图 消费者年收入统计表 消费者年收入统计表 请你根据以上信息,回答下列问题: (1)求出统计表中的 (2)打算购买住房面积小于100平方米的消费者  人数占被调查人数的百分比为 ; 人数占被调查人数的百分比为 ;(3)求被调查的消费者平均每人年收入为多少万元? 19、(本题满分6分)如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC. ⑴ 求证:AD=AE; ⑵ 若AD=8,DC=4,求AB的长. 20、(本题满分8分)在不透明的袋中有大小、形状和质地等完全相同的小球,它们分别标有数字-1、-2、1、2.从袋中任意摸出一小球(不放回),将袋中的小球搅匀后,再从袋中摸出另一个小球. (1)请你表示摸出小球上的数字可能出现的所有结果; (2)若规定:如果摸出的两个小球上的数字都是方程x2-3x+2=0的根,则小明赢.如果摸出的两个小球上的数字都不是方程x2-3x+2=0的根,则小亮赢.你认为这个游戏规则对小明、小亮双方公平吗?请说明理由. 21、(本题满分8分)某超市规定:凡一次购买大米180kg以上(含180kg)可以享受折扣价格,否则只能按原价付款.王师傅到该超市买大米,发现自己准备购买的数量只能按原价付款,且需要500元,于是他多买了40kg,就可全部享受折扣价,也只需付款500元. 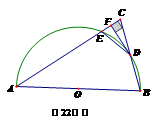 (1)求王师傅原来准备购买大米的数量x(kg)的范围; (1)求王师傅原来准备购买大米的数量x(kg)的范围;(2)若按原价购买4kg与按折扣价购买5kg大米的付款数相同,那么王师傅原 来准备购买多少kg大米. 22、(本题满分8分)如图,已知在△ABC中,AB=AC,以AB为直径的半圆 ⊙O与边BC交于点D,与边AC交于点E,过点D作DF⊥AC于F.  (1)求证:DF为⊙O的切线;(2)若DE= ,AB= ,求AE的长. (1)求证:DF为⊙O的切线;(2)若DE= ,AB= ,求AE的长.23、(本题满分10分)如图,港口B位于港口O正西方向120海里外,小岛C位 于港口O北偏西60°的方向.一艘科学考察船从港口O出发,沿北偏西30°的 OA方向以20海里/小时的速度驶离港口O.同时一艘快艇从港口B出发,沿北 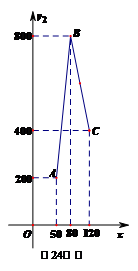 偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给 偏东30°的方向以60海里/小时的速度驶向小岛C,在小岛C用1小时装补给物资后,立即按原来的速度给考察船送去. ⑴快艇从港口B到小岛C需要多少时间? ⑵快艇从小岛C出发后最少需要多少时间才能和考察船相遇? 24、(本题满分10分)某品牌专卖店准备采购数量相同的男女情侣衬衫,并以 相同的销售价x(元)进行销售,男衬衫的进价为30元,当定价为50元时, 月销售量为120件,售价不超过100元时,价格每上涨1元,销量减少1件; 售价超过100元时,超过100元的部分,每上涨1元,销量减少2件.受投放 量限制衬衫公司要求该专卖店每种衬衫每月订购件数不得低于30件且不得超 过120件.该品牌专卖店销售男衬衫利润为y1 (元),销售女衬衫的月利润为y2(元),且y2与x间的函数关系如图所示,AB、BC都是线段,,销售这两种衬衫的月利润W(元)是y1与y2的和. (1)求y1、y2与x间的函数关系式;(2)求出W关于x的函数关系式; (3)该专卖店经理应该如何采购,如何定价,才能使每月获得的总收益W最大?说明理由. 25、(本题满分10分)如图,在平面直角坐标系中,四边形OABC是平行四边形.直线L经过O、C两点.点A的坐标为(8,0),点B的坐标为(11,4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C﹣B相交于点M.当Q、M两点相遇时,P、Q两点停止运动,设点P、Q运动的时间为t秒(t>0).△MPQ的面积为S. (1)点C的坐标为 ,直线L的解析式为 . (2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围. (3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值. (4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线L相交于点N.试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值. 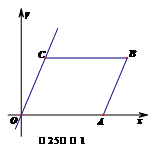 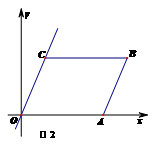 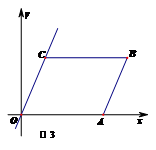 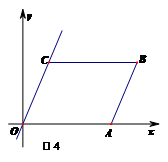 2018年株洲中考数学模拟试题参考答案 一、 选择题: 1、 B;2、D;3、D;4、B;5、C;6、C;7、D;8、B. 二、 填空题: 9、;10、-;11、x2+4x+5;12、50°;13、2cm;14、;15、25°;16、4. 三、解答题: 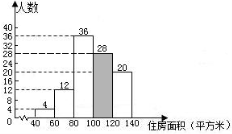 17、解:解不等式①,得x≤8,解不等式②,得x>-,所以,原不等式组的解集是-<x≤8. 17、解:解不等式①,得x≤8,解不等式②,得x>-,所以,原不等式组的解集是-<x≤8.18、解:(1) (2)52%; 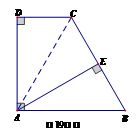 (3) (3)故被调查的消费者平均每人年收入为7.5万元. 19、解:(1)连接AC,∵AB∥CD,∴∠ACD=∠BAC,∵AB=BC, ∴∠ACB=∠BAC,∴∠ACD=∠ACB ,∵AD⊥DC, AE⊥BC, ∴∠D=∠AEC=900 ,∵AC=AC,∴△ADC≌△AEC,∴AD=AE, (2)由(1)知:AD=AE ,DC=EC, 设AB=x,则BE=x-4 ,AE=8, 在Rt△ABE中, ∠AEB=900, 由勾股定理得: 20、解:(1)可能出现的所有结果如下:
共12种结果; (2)∵x2﹣3x+2=0,∴(x﹣1)(x﹣2)=0,∴x1=1,x2=2; ∵摸出的两个小球上的数字都是方程x2﹣3x+2=0的根的可能一共有2种, 摸出的两个小球上的数字都不是方程的根的可能一共有2种,∴P小明赢= = ,P小亮赢= = , ∴游戏公平. 21、解:(1)x<180;x+40≥180,解得:140≤x<180; (2)设王师傅原来准备买大米x千克,原价为元;折扣价为元. 据题意列方程为:4·= 5·,解得:x=160,经检验x=160是方程的解. 答:王师傅原来准备买160千克大米. 22、证明:(1)连接AD,OD,∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=DC,∵OA=OB,∴OD∥AC,∵DF⊥AC,∴DF⊥OD,∴DF为⊙O的切线; 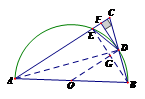 (2)连接BE交OD于G,∵AC=AB,AD⊥BCED⊥BD,∴∠EAD=∠BAD,∴ (2)连接BE交OD于G,∵AC=AB,AD⊥BCED⊥BD,∴∠EAD=∠BAD,∴∴OG=AE.在Rt△DGB和Rt△OGB中, BD2﹣DG2=BO2﹣OG2,∴()2-(-OG)2=BO2-OG2, 解得:OG= .∴AE=2OG= . 23、解:(1)由题意可知:∠CBO=60°,∠COB=30°. ∴∠BCO=90°.在Rt△BCO中,∵OB=120,∴BC=60,OC= 60.∴快艇从港口B到小岛C的时间为:60÷60=1(小时). 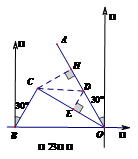 (2)设快艇从C岛出发后最少要经过x小时才能和考查船在OA上的D处相遇,则CD=60x.∵考查船与快艇是同时出发,∴考查船从O到D行驶了(x+2)小时,∴OD=20(x+2).过C作CH⊥OA,垂足为H,在△OHC中,∵∠COH=30°,∴CH=30,OH=90.∴DH=OH﹣OD=90﹣20(x+2)=50﹣20x.在Rt△CHD中,CH2+DH2=CD2,∴(30)2+(50﹣20x)2=(60x)2. (2)设快艇从C岛出发后最少要经过x小时才能和考查船在OA上的D处相遇,则CD=60x.∵考查船与快艇是同时出发,∴考查船从O到D行驶了(x+2)小时,∴OD=20(x+2).过C作CH⊥OA,垂足为H,在△OHC中,∵∠COH=30°,∴CH=30,OH=90.∴DH=OH﹣OD=90﹣20(x+2)=50﹣20x.在Rt△CHD中,CH2+DH2=CD2,∴(30)2+(50﹣20x)2=(60x)2.整理得:8x2+5x﹣13=0.解得:x1=1,x2=- .∵x>0,∴x=1. 答:快艇后从小岛C出发后最少需要1小时才能和考查船相遇. 24、解:(1)由已知可求得: 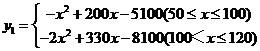 ; ;(2) 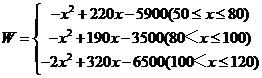 ; ;(3)配方得: 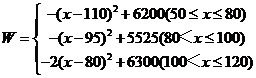 , ,当50≤x≤80时,W随x增大而增大,所以x=80时,W最大=5300; 当80<x<100时,x=95,W最大=5525; 当100<x<120时,W随x增大而减小,而x=100时,W=5500; 综上所述,当x=95时,W最大且W最大=5525, 故专卖店经理应该将两种衬衫定价为95元,进货数量确定为120﹣(95﹣50)=75件时,专卖店月获利最大且为5525元. 25、解:(1)由题意知:点A的坐标为(8,0),点B的坐标为(11.4), 且OA=BC,故C点坐标为C(3,4),设直线l的解析式为y=kx,将C点坐标代入y=kx,解得k= , ∴直线l的解析式为y= x;故答案为:(3,4),y= x; 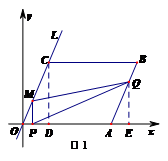 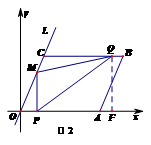 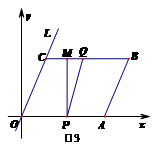  (2)根据题意,得OP=t,AQ=2t.分四种情况讨论: ①当0<t≤时,如图1,M点的坐标是(t,t).过点C作CD⊥x轴于D,过点Q作QE⊥x轴于E,可得△AEQ∽△ODC,∴ = = ,∴ = = ,∴AE = ,EQ= t,∴Q点的坐标是(8+ t,t),∴PE=8+t-t= 8+t,∴S= ·MP·PE= ·t·(8+t)= t2+ t; ②当<t≤3时,如图2,过点Q作QF⊥x轴于F,∵BQ=2t﹣5,∴OF=11﹣(2t﹣5)=16﹣2t, ∴Q点的坐标是(16﹣2t,4),∴PF=16﹣2t﹣t=16﹣3t, ∴S= ·MP·PF= ·t·(16-3t)= -2t2+t, ③当点Q与点M相遇时,16﹣2t=t,解得t = .当3<t<时,如图3,MQ=16﹣2t﹣t=16﹣3t,MP=4.S= ·MP·PF = ·4·(16-3t)=﹣6t+32; (3)解:① 当 ②当 ∴当 ③当 又∵当 综上所述,当 (4)M、Q在BC边上运动且没有相遇时,如图4,CM=t-3,BQ= 2t-5,MN= (t-3),∴MQ= 8-(t-3)-(2t-5)= 16-3t,∴只有(t-3)=16-3t,即当t= 时,△QMN为等腰三角形. (责任编辑:admin) |
