|
☆☆☆ 点击下载试题 ☆☆☆ 由于格式问题此试题可能会出现乱码的情况 为了方便您阅读请点击右上角的全屏查看 2018东营市胜利一中八年级期末数学试卷 一、选择题：（本大题共10小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项涂在答题卡上.每小题选对得3分，选错、不选或选出的答案超过一个均记零分．） 1．点P（1，2）关于原点的对称点P′的坐标为（ ） A．（2，1） B．（﹣1，﹣2） C．（1，﹣2） D．（﹣2，﹣1） 2．若二次函数y=2x2的图象经过点P（1，a），则a的值为（ ） A．  B．1 C．2 D．43．（东营中考数学）如图，⊙O的直径CD垂直弦AB于点E，且CE=2，DE=8，则AB的长为（ ）  A．2 B．4 C．6 D．8 4．若抛物线y=x2﹣2x+c与y轴的交点为（0，﹣3），则下列说法不正确的是（ ） A．抛物线开口向上 B．抛物线的对称轴是x=1 C．当x=1时，y的最大值为4 D．抛物线与x轴的交点为（﹣1，0），（3，0） 5．（东营中考数学）有20张背面完全一样的卡片，其中8张正面印有天鹅湖风光，7张正面印有黄河入海口自然风景，5张正面印有孙武湖景色．把这些卡片的背面朝上，搅匀后从中随机抽出一张卡片，抽到正面是天鹅湖风光卡片的概率是（ ） A．  B． C． D． 6．如图，E、F分别是正方形ABCD的边AB、BC上的点，且BE=CF，连接CE、DF，将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置，则旋转角为（ ）  A．30° B．45° C．60° D．90° 7．（东营中考数学）河北省赵县的赵州桥的桥拱是近似的抛物线形，建立如图所示的平面直角坐标系，其函数的关系式为y=﹣  x2，当水面离桥拱顶的高度DO是4m时，这时水面宽度AB为（ ） A．﹣20m B．10m C．20m D．﹣10m 8．（东营中考数学）将等腰直角三角形AOB按如图所示放置，然后绕点O逆时针旋转90°至△A′OB′的位置，点B的横坐标为2，则点A′的坐标为（ ）  A．（1，1） B．（  ） C．（﹣1，1） D．（ ）9（东营中考数学）．2013年“五•一”期间，小明与小亮两家准备从东营港、黄河入海口、龙悦湖中选择一景点游玩，小明与小亮通过抽签方式确定景点，则两家抽到同一景点的概率是（ ） A．  B． C． D． 10．如图，在平面直角坐标系中，⊙M与x轴相切于点A（8，0），与y轴分别交于点B（0，4）和点C（0，16），则圆心M到坐标原点O的距离是（ ）  A．10 B．8  C．4 D．2 二、（东营中考数学）填空题：（本大题共8个小题，11-14每小题3分，15-18每小题3分，共28分．） 11．若在“正三角形、平行四边形、菱形、正五边形、正六边形”这五种图形中随机抽取一种图形，则抽到的图形属于中心对称图形的概率是 ． 12．已知一个扇形的半径为60cm，圆心角为150°，用它围成一个圆锥的侧面，那么圆锥的底面半径为 cm． 13．如图，△ABC内接于⊙O，∠OAB=20°，则∠C的度数为 ．  14．对于函数y=x2+2x+1，当1＜x＜2时，y随x的增大而 （填写“增大”或“减小”）． 15．半径为1的圆的内接正三角形的边长为 ． 16．如图，是一个半圆和抛物线的一部分围成的“芒果”，已知点A、B、C、D分别是“芒果”与坐标轴的交点，AB是半圆的直径，抛物线的解析式为y= 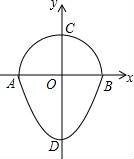 x2﹣，则图中CD的长为 ． 17．（东营中考数学）若函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是 ． 18．如图，在△ABC中，AB=4cm，BC=2cm，∠ABC=30°，把△ABC以点B为中心按逆时针方向旋转，使点C旋转到AB边的延长线上的点C′处，那么AC边扫过的图形（图中阴影部分）的面积是 cm2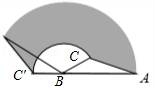．  三、解答题：（本大题共5个小题，共62分．解答要写出必要的文字说明、证明过程或演算步骤）． 19．（东营中考数学）某学校为了增强学生体质，决定开设以下体育课外活动项目：A．篮球 B．乒乓球C．羽毛球 D．足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题： （1）这次被调查的学生共有 人； （2）请你将条形统计图（2）补充完整； （3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答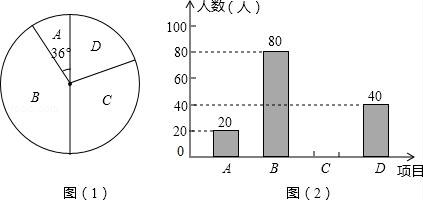）  20．（东营中考数学）如图，在边长均为1的正方形网格纸上有一个△ABC，顶点A、B、C及点O均在格点上，请按要求完成以下操作或运算： （1）将△ABC向上平移4个单位，得到△A1B1C1（不写作法，但要标出字母）； （2）将△ABC绕点O旋转180°，得到△A2B2C2（不写作法，但要标出字母）； （3）求点A绕着点O旋转到点A2所经过的路径长．  21（东营中考数学）．如图，AB为⊙O的直径，点C为⊙O上一点，若∠BAC=∠CAM，过点C作直线l垂直于射线AM，垂足为点D． （1）试判断CD与⊙O的位置关系，并说明理由； （2）若直线l与AB的延长线相交于点E，⊙O的半径为3，并且∠CAB=30°，求CE的长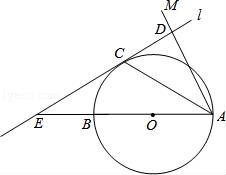．  22．（东营中考数学）某果园有100棵橙子树，平均每棵树结600个橙子，现准备多种一些橙子树以提高果园产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少．根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子，假设果园多种了x棵橙子树． （1）直接写出平均每棵树结的橙子个数y（个）与x之间的关系； （2）果园多种多少棵橙子树时，可使橙子的总产量最大？最大为多少个？ 23．如图，AB是⊙O的直径，AM和BN是它的两条切线，DE切⊙O于点E，交AM于点D，交BN于点C， （1）求证：OD∥BE； （2）如果OD=6cm，OC=8cm，求CD的长．  24．（东营中考数学）如图，在平面直角坐标系中，直线y=﹣2x+10与x轴，y轴相交于A，B两点，点C的坐标是（8，4），连接AC，BC． （1）求过O，A，C三点的抛物线的解析式，并判断△ABC的形状； （2）动点P从点O出发，沿OB以每秒2个单位长度的速度向点B运动；同时，动点Q从点B出发，沿BC以每秒1个单位长度的速度向点C运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t秒，当t为何值时，PA=QA？ （3）在抛物线的对称轴上，是否存在点M，使以A，B，M为顶点的三角形是等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．  东营中考数学参考答案与试题解析 一、选择题：（本大题共10小题，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项涂在答题卡上.每小题选对得3分，选错、不选或选出的答案超过一个均记零分．） 1．点P（1，2）关于原点的对称点P′的坐标为（ ） A．（2，1） B．（﹣1，﹣2） C．（1，﹣2） D．（﹣2，﹣1） 【考点】R6：关于原点对称的点的坐标． 【分析】根据两个点关于原点对称时，它们的坐标符号相反可得答案． 【解答】解：点P（1，2）关于原点的对称点P′的坐标为（﹣1，﹣2）， 故选：B． 2．（东营中考数学）若二次函数y=2x2的图象经过点P（1，a），则a的值为（ ） A． B．1 C．2 D．4【考点】H5：二次函数图象上点的坐标特征． 【分析】直接把P（1，a）代入y=2x2中可计算出a的值． 【解答】解：把P（1，a）代入y=2x2得a=2×1=2． 故选C． 3．（东营中考数学）如图，⊙O的直径CD垂直弦AB于点E，且CE=2，DE=8，则AB的长为（ ）  A．2 B．4 C．6 D．8 【考点】M2：垂径定理；KQ：勾股定理． 【分析】根据CE=2，DE=8，得出半径为5，在直角三角形OBE中，由勾股定理得BE，根据垂径定理得出AB的长． 【解答】解：∵CE=2，DE=8， ∴OB=5， ∴OE=3， ∵AB⊥CD， ∴在△OBE中，得BE=4， ∴AB=2BE=8． 故选：D． 4．若抛物线y=x2﹣2x+c与y轴的交点为（0，﹣3），则下列说法不正确的是（ ） A．抛物线开口向上 B．抛物线的对称轴是x=1 C．当x=1时，y的最大值为4 D．抛物线与x轴的交点为（﹣1，0），（3，0） 【考点】（东营中考数学）H3：二次函数的性质． 【分析】把（0，﹣3）代入抛物线解析式求c的值，然后再求出顶点坐标、与x轴的交点坐标． 【解答】解：把（0，﹣3）代入y=x2﹣2x+c中得c=﹣3， 抛物线为y=x2﹣2x﹣3=（x﹣1）2﹣4=（x+1）（x﹣3）， 所以：抛物线开口向上，对称轴是x=1， 当x=1时，y的最小值为﹣4， 与x轴的交点为（﹣1，0），（3，0）；C错误． 故选C． 5．（东营中考数学）有20张背面完全一样的卡片，其中8张正面印有天鹅湖风光，7张正面印有黄河入海口自然风景，5张正面印有孙武湖景色．把这些卡片的背面朝上，搅匀后从中随机抽出一张卡片，抽到正面是天鹅湖风光卡片的概率是（ ） A． B． C． D．【考点】X4：概率公式． 【分析】根据随机事件概率大小的求法，找准两点：①符合条件的情况数目；②全部情况的总数；二者的比值就是其发生的概率的大小． 【解答】解：共有图片20张，天鹅湖风光卡片8张，抽到正面是天鹅湖风光卡片的概率是：  =．故选C． 6．（东营中考数学）如图，E、F分别是正方形ABCD的边AB、BC上的点，且BE=CF，连接CE、DF，将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置，则旋转角为（ ）  A．30° B．45° C．60° D．90° 【考点】R2：旋转的性质． 【分析】由题意得到D对应点为C，连接OC，OD，∠DOC即为旋转角，利用正方形性质求出即可． 【解答】（东营中考数学）解：∵正方形ABCD，O为正方形的中心， ∴OD=OC，OD⊥OC， ∴∠DOC=90°， 由题意得到D对应点为C，连接OC，OD，∠DOC即为旋转角， 则将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置，旋转角为90°， 故选D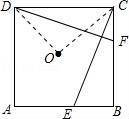．  7．（东营中考数学）河北省赵县的赵州桥的桥拱是近似的抛物线形，建立如图所示的平面直角坐标系，其函数的关系式为y=﹣  x2，当水面离桥拱顶的高度DO是4m时，这时水面宽度AB为（ ） A．﹣20m B．10m C．20m D．﹣10m 【考点】HE：二次函数的应用． 【分析】根据题意，把y=﹣4直接代入解析式即可解答． 【解答】解：根据题意B的纵坐标为﹣4， 把y=﹣4代入y=﹣  x2，得x=±10， ∴A（﹣10，﹣4），B（10，﹣4）， ∴AB=20m． 即水面宽度AB为20m． 故选C． 8．（东营中考数学）将等腰直角三角形AOB按如图所示放置，然后绕点O逆时针旋转90°至△A′OB′的位置，点B的横坐标为2，则点A′的坐标为（ ） A．（1，1） B．（ ） C．（﹣1，1） D．（ ）【考点】（东营中考数学）R7：坐标与图形变化﹣旋转． 【分析】过点A作AC⊥OB于C，过点A′作A′C′⊥OB′于C′，根据等腰直角三角形的性质求出OC=AC，再根据旋转的性质可得OC′=OC，A′C′=AC，然后写出点A′的坐标即可． 【解答】解：如图，过点A作AC⊥OB于C，过点A′作A′C′⊥OB′于C′， ∵△AOB是等腰直角三角形，点B的横坐标为2， ∴OC=AC=  ×2=1，∵△A′OB′是△AOB绕点O逆时针旋转90°得到， ∴OC′=OC=1，A′C′=AC=1， ∴点A′的坐标为（﹣1，1）． 故选C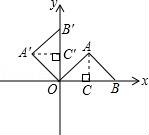．  9．（东营中考数学）2013年“五•一”期间，小明与小亮两家准备从东营港、黄河入海口、龙悦湖中选择一景点游玩，小明与小亮通过抽签方式确定景点，则两家抽到同一景点的概率是（ ） A．  B． C． D． 【考点】X6：列表法与树状图法． 【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两家抽到同一景点的情况，再利用概率公式求解即可求得答案． 【解答】解：用A、B、C表示：东营港、黄河入海口、龙悦湖； 画树状图得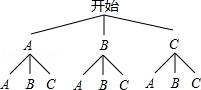：  ∵共有9种等可能的结果，则两家抽到同一景点的有3种情况， ∴则两家抽到同一景点的概率是：  = ．故选A． 10．（东营中考数学）如图，在平面直角坐标系中，⊙M与x轴相切于点A（8，0），与y轴分别交于点B（0，4）和点C（0，16），则圆心M到坐标原点O的距离是（ ） A．10 B．8 C．4 D．2【考点】MC：切线的性质；D5：坐标与图形性质． 【分析】如图连接BM、OM，AM，作MH⊥BC于H，先证明四边形OAMH是矩形，根据垂径定理求出HB，在RT△AOM中求出OM即可． 【解答】解：如图连接BM、OM，AM，作MH⊥BC于H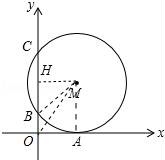．  ∵⊙M与x轴相切于点A（8，0）， ∴AM⊥OA，OA=8， ∴∠OAM=∠MH0=∠HOA=90°， ∴四边形OAMH是矩形， ∴AM=OH， ∵MH⊥BC， ∴HC=HB=6， ∴OH=AM=10， 在RT△AOM中，OM=  = =2 ．故选D． 二、（东营中考数学）填空题：（本大题共8个小题，11-14每小题3分，15-18每小题3分，共28分．） 11．若在“正三角形、平行四边形、菱形、正五边形、正六边形”这五种图形中随机抽取一种图形，则抽到的图形属于中心对称图形的概率是  ．【考点】X4：概率公式；R5：中心对称图形． 【分析】根据中心对称图形的定义得到平行四边形、菱形和正六边形是中心对称图形，于是利用概率公式可计算出抽到的图形属于中心对称图形的概率． 【解答】解：在“正三角形、平行四边形、菱形、正五边形、正六边形”这五种图形中，平行四边形、菱形和正六边形是中心对称图形， 所以这五种图形中随机抽取一种图形，则抽到的图形属于中心对称图形的概率= ．故答案为： ．12．（东营中考数学）已知一个扇形的半径为60cm，圆心角为150°，用它围成一个圆锥的侧面，那么圆锥的底面半径为 25 cm． 【考点】MP：圆锥的计算． 【分析】首先利用扇形的弧长公式求得扇形的弧长，然后利用圆的周长公式即可求解． 【解答】解：扇形的弧长是：  =50πcm，设底面半径是rcm，则2πr=50π， 解得：r=25． 故答案是：25． 13．如图，△ABC内接于⊙O，∠OAB=20°，则∠C的度数为 70° ．  【考点】M5：圆周角定理． 【分析】（东营中考数学）由△ABC内接于⊙O，∠OAB=20°，根据等腰三角形的性质，即可求得∠OBA的度数，∠AOB的度数，又由圆周角定理，求得∠ACB的度数． 【解答】解：∵∠OAB=20°，OA=OB， ∴∠OBA=∠OAB=20°， ∴∠AOB=180°﹣∠OAB﹣∠OBA=140°， ∴∠ACB= ∠AOB=70°．故答案为70°． 14．（东营中考数学）对于函数y=x2+2x+1，当1＜x＜2时，y随x的增大而 增大 （填写“增大”或“减小”）． 【考点】H3：二次函数的性质． 【分析】由y=x2+2x+1=（x+1）2知函数图象开口向上且当x＞﹣1时，y随x的增大而增大． 【解答】解：∵y=x2+2x+1=（x+1）2， ∴当x＞﹣1时，y随x的增大而增大， 则当1＜x＜2时，y随x的增大而增大， 故答案为：增大． 15．（东营中考数学）半径为1的圆的内接正三角形的边长为  ．【考点】MM：正多边形和圆． 【分析】欲求△ABC的边长，把△ABC中BC边当弦，作BC的垂线，在Rt△BOD中，求BD的长；根据垂径定理知：BC=2BD，从而求正三角形的边长． 【解答】解：如图所示． 在Rt△BOD中，OB=1，∠OBD=30°， ∴BD=cos30°×OB=  ×1=．∵BD=CD， ∴BC=2BD=2× = ．故它的内接正三角形的边长为 ．故答案为： ． 16．如图，是一个半圆和抛物线的一部分围成的“芒果”，已知点A、B、C、D分别是“芒果”与坐标轴的交点，AB是半圆的直径，抛物线的解析式为y=  x2﹣，则图中CD的长为  ． 【考点】（东营中考数学）HA：抛物线与x轴的交点． 【分析】首先令y=  x2﹣=0，即可求出AB的长，进而得到OC的长，令x=0，求出y的值，进而得到OD的长，由CD=OC+DO即可求出答案．【解答】解：令y= x2﹣=0，解得x=1或﹣1， 即AB=2， 故CO=1， 令x=0，解得y=﹣ ，即OD= ，所以CD=CO+OD=1+ = ，故答案为 ．17．（东营中考数学）若函数y=mx2+2x+1的图象与x轴只有一个公共点，则常数m的值是 0或1 ． 【考点】HA：抛物线与x轴的交点；F5：一次函数的性质． 【分析】需要分类讨论： ①若m=0，则函数为一次函数； ②若m≠0，则函数为二次函数．由抛物线与x轴只有一个交点，得到根的判别式的值等于0，且m不为0，即可求出m的值． 【解答】解：①若m=0，则函数y=2x+1，是一次函数，与x轴只有一个交点； ②若m≠0，则函数y=mx2+2x+1，是二次函数． 根据题意得：△=4﹣4m=0， 解得：m=1． 故答案为：0或1． 18．（东营中考数学）如图，在△ABC中，AB=4cm，BC=2cm，∠ABC=30°，把△ABC以点B为中心按逆时针方向旋转，使点C旋转到AB边的延长线上的点C′处，那么AC边扫过的图形（图中阴影部分）的面积是 5π cm2．  【考点】MO：扇形面积的计算． 【分析】根据题意可知该阴影部分的面积为两个扇形面积的差，分别计算出两个扇形的面积相减即可得到阴影部分的面积． 【解答】（东营中考数学）解：∵∠ABC=∠A′BC′=30°， ∴△ABC以点B为中心按逆时针方向旋转了180°﹣30°=150°， ∴按反方向旋转相同的角度即可得到阴影部分为两个扇形面积的差， ∵AB=4cm，BC=2cm ∴S阴影部分=  =5π．故答案为：5π． 三、（东营中考数学）解答题：（本大题共5个小题，共62分．解答要写出必要的文字说明、证明过程或演算步骤）． 19．某学校为了增强学生体质，决定开设以下体育课外活动项目：A．篮球 B．乒乓球C．羽毛球 D．足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题： （1）这次被调查的学生共有 200 人； （2）请你将条形统计图（2）补充完整； （3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答） 【考点】（东营中考数学）VC：条形统计图；VB：扇形统计图；X6：列表法与树状图法． 【分析】（1）由喜欢篮球的人数除以所占的百分比即可求出总人数； （2）由总人数减去喜欢A，B及D的人数求出喜欢C的人数，补全统计图即可； （3）根据题意列出表格，得出所有等可能的情况数，找出满足题意的情况数，即可求出所求的概率． 【解答】解：（1）根据题意得：20÷  =200（人），则这次被调查的学生共有200人； （2）补全图形，如图所示：  （3）列表如下：
所有等可能的结果为12种，其中符合要求的只有2种， 则P=  =．20．（东营中考数学）如图，在边长均为1的正方形网格纸上有一个△ABC，顶点A、B、C及点O均在格点上，请按要求完成以下操作或运算： （1）将△ABC向上平移4个单位，得到△A1B1C1（不写作法，但要标出字母）； （2）将△ABC绕点O旋转180°，得到△A2B2C2（不写作法，但要标出字母）； （3）求点A绕着点O旋转到点A2所经过的路径长．  【考点】（东营中考数学）R8：作图﹣旋转变换；MN：弧长的计算；Q4：作图﹣平移变换． 【分析】（1）根据图形平移的性质画出平移后的△A1B1C1即可； （2）根据图形旋转的性质画出△ABC绕点O旋转180°后得到的△A2B2C2； （3）根据弧长的计算公式列式即可求解． 【解答】解：（1）△A1B1C1如图所示； （2）△A2B2C2如图所示： （3）∵OA=4，∠AOA2=180°， ∴点A绕着点O旋转到点A2所经过的路径长为 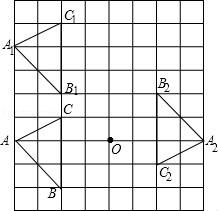 =4π． 21．（东营中考数学）如图，AB为⊙O的直径，点C为⊙O上一点，若∠BAC=∠CAM，过点C作直线l垂直于射线AM，垂足为点D． （1）试判断CD与⊙O的位置关系，并说明理由； （2）若直线l与AB的延长线相交于点E，⊙O的半径为3，并且∠CAB=30°，求CE的长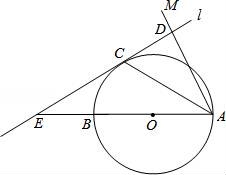．  【考点】MD：切线的判定；T7：解直角三角形． 【分析】（1）连接OC，根据OA=OC，推出∠BAC=∠OCA，求出∠OCA=∠CAM，推出OC∥AM，求出OC⊥CD，根据切线的判定推出即可； （2）根据OC=OA推出∠BAC=∠ACO，求出∠COE=2∠CAB=60°，在Rt△COE中，根据CE=OC•tan60°求出即可． 【解答】（东营中考数学）解：（1）直线CD与⊙O相切． 理由如下：连接OC． ∵OA=OC， ∴∠BAC=∠OCA， ∵∠BAC=∠CAM， ∴∠OCA=∠CAM， ∴OC∥AM， ∵CD⊥AM， ∴OC⊥CD， ∵OC为半径， ∴直线CD与⊙O相切． （2）∵OC=OA， ∴∠BAC=∠ACO， ∵∠CAB=30°， ∴∠COE=2∠CAB=60°， ∴在Rt△COE中，OC=3，CE=OC•tan60°= 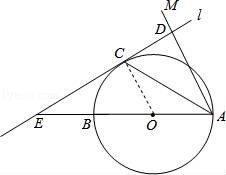 ． 22．（东营中考数学）某果园有100棵橙子树，平均每棵树结600个橙子，现准备多种一些橙子树以提高果园产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少．根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子，假设果园多种了x棵橙子树． （1）直接写出平均每棵树结的橙子个数y（个）与x之间的关系； （2）果园多种多少棵橙子树时，可使橙子的总产量最大？最大为多少个？ 【考点】HE：二次函数的应用． 【分析】（1）根据每多种一棵树，平均每棵树就会少结5个橙子列式即可； （2）根据题意列出函数解析式，利用配方法把二次函数化为顶点式，根据二次函数的性质进行解答即可． 【解答】（东营中考数学）解：（1）平均每棵树结的橙子个数y（个）与x之间的关系为：y=600﹣5x（0≤x＜120）； （2）设果园多种x棵橙子树时，可使橙子的总产量为w， 则w= =﹣5x2+100x+60000 =﹣5（x﹣10）2+60500， ∵a=﹣5＜0， ∴w的最大值是60500， 则果园多种10棵橙子树时，可使橙子的总产量最大，最大为60500个． 23．（东营中考数学）如图，AB是⊙O的直径，AM和BN是它的两条切线，DE切⊙O于点E，交AM于点D，交BN于点C， （1）求证：OD∥BE； （2）如果OD=6cm，OC=8cm，求CD的长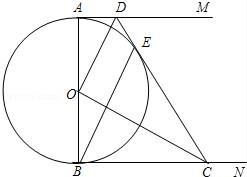．  【考点】MC：切线的性质；KQ：勾股定理． 【分析】（东营中考数学）（1）首先连接OE，由AM和DE是它的两条切线，易得∠ADO=∠EDO，∠DAO=∠DEO=90°，由切线长定理，可得∠AOD=∠EOD=  ∠AOE，∠AOD=∠ABE，根据同位角相等，两直线平行，即可证得OD∥BE；（2）由（1），易证得∠EOD+∠EOC=90°，然后利用勾股定理，即可求得CD的长． 【解答】（1）证明：连接OE， ∵AM、DE是⊙O的切线，OA、OE是⊙O的半径， ∴∠ADO=∠EDO，∠DAO=∠DEO=90°，… ∴∠AOD=∠EOD= ∠AOE，∵∠ABE= ∠AOE，∴∠AOD=∠ABE， ∴OD∥BE； … （2）（东营中考数学）解：由（1）得：∠AOD=∠EOD= ∠AOE，同理，有：∠BOC=∠EOC= ∠BOE，∴∠AOD+∠EOD+∠BOC+∠EOC=180°， ∴∠EOD+∠EOC=90°， ∴△DOC是直角三角形，… ∴CD= 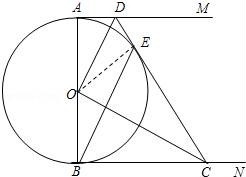 =10（cm）．… 24．（东营中考数学）如图，在平面直角坐标系中，直线y=﹣2x+10与x轴，y轴相交于A，B两点，点C的坐标是（8，4），连接AC，BC． （1）求过O，A，C三点的抛物线的解析式，并判断△ABC的形状； （2）动点P从点O出发，沿OB以每秒2个单位长度的速度向点B运动；同时，动点Q从点B出发，沿BC以每秒1个单位长度的速度向点C运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t秒，当t为何值时，PA=QA？ （3）在抛物线的对称轴上，是否存在点M，使以A，B，M为顶点的三角形是等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．  【考点】HF：二次函数综合题． 【分析】（1）先确定出点A，B坐标，再用待定系数法求出抛物线解析式；用勾股定理逆定理判断出△ABC是直角三角形； （2）根据运动表示出OP=2t，CQ=10﹣t，判断出Rt△AOP≌Rt△ACQ，得到OP=CQ即可； （3）分三种情况用平面坐标系内，两点间的距离公式计算即可， 【解答】（东营中考数学）解：（1）∵直线y=﹣2x+10与x轴，y轴相交于A，B两点， ∴A（5，0），B（0，10）， ∵抛物线过原点， ∴设抛物线解析式为y=ax2+bx， ∵抛物线过点A（5，0），C（8，4）， ∴  ，∴  ，∴抛物线解析式为y=  x2﹣ x，∵A（5，0），B（0，10），C（8，4）， ∴AB2=52+102=125，BC2=82+（10﹣4）2=100，AC2=42+（8﹣5）2=25， ∴AC2+BC2=AB2， ∴△ABC是直角三角形． （2）如图1，  当P，Q运动t秒，即OP=2t，CQ=10﹣t时， 由（1）得，AC=OA，∠ACQ=∠AOP=90°， 在Rt△AOP和Rt△ACQ中，  ，∴Rt△AOP≌Rt△ACQ， ∴OP=CQ， ∴2t=10﹣t， ∴t=  ，∴当运动时间为  时，PA=QA；（3）存在， ∵y=  x2﹣ x，∴抛物线的对称轴为x= ，∵A（5，0），B（0，10）， ∴AB=5  设点M（ ，m），①若BM=BA时， ∴（ ）2+（m﹣10）2=125，∴m1=  ，m2= ，∴M1（  ， ），M2（，），②若AM=AB时， ∴（ ）2+m2=125，∴m3=  ，m4=﹣，∴M3（  ， ），M4（，﹣），③若MA=MB时， ∴（ ﹣5）2+m2=（）2+（10﹣m）2，∴m=5， ∴M（ ，5），此时点M恰好是线段AB的中点，构不成三角形，舍去，∴点M的坐标为：M1（ ，），M2（，），M3（，），M4（，﹣），(责任编辑：admin) |