|
☆☆☆ 点击下载试题 ☆☆☆  2018年临汾中考数学冲刺试卷【精选word版】由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ 一、选择题(本大题共10小题，每小题3分，共30分) 1．－的倒数是( ) A．－ B．－ C. D. 2．下列说法正确的是（ ） A．“任意画出一个圆，它是中心对称图形”是随机事件 B．为了解我省中学生的体能情况，应采用普查的方式 C．天气预报明天下雨的概率是99%，说明明天一定会下雨 D．任意掷一枚质地均匀的硬币10次，正面朝上的次数不一定是5次 3．下列运算正确的是( ) A．(ab)2＝ab2 B．3a＋2a2＝5a2 C．2(a＋b)＝2a＋b D．a·a＝a2 4．如图是由5个相同的小正方体组成的立体图形，这个立体图形的俯视图是( )  5. 如图，直线m∥n，Rt△ABC的顶点A在直线n上，∠C=90°，AB，CB分别交直线m于点D和点E，且DB=DE，若∠B=25°，则∠1的度数为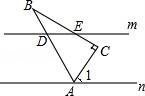（ ）  A．60° B．65°  C．70° D．75°6．小敏和小华在某次各科满分均为100分的期末测试中，各科成绩的平均分  相同．小敏想和小华再比较一下两人中谁的各科成绩更加均衡，则他需要分别计算两人各科成绩的（ ）A．加权平均数 B．方差 C．众数 D．中位数 7．．如图6×7的方格中，点A，B，C，D是格点，线段CD是由线段AB位似放大得到的，则 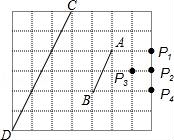它们的位似中心是（ ） A．P1 B．P2 C．P3 D．P4 8．按照山西省“改薄工程”规划，我省5年投入85亿元用于改造农村县(市、区)薄弱学校，促进义务教育均衡发展，其中某项“改薄工程”建设，甲队单独完成需要20天，若由甲队先做13天，则剩下的工程由甲、乙两队合作3天完成．问乙队单独完成这项工程需要多少天？若设乙队单独完成这项工程需要x天，根据题意可列方程为( ) A．13＋3＋x＝20 B.＋3(＋)＝1 C.＋＝1 D．(1－)＋x＝3 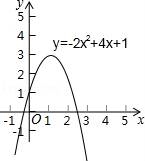 9．在求解一元二次方程﹣2x2+4x+1=0的两个根x1和x2时，某同学使用电脑软件绘制了如图所示的二次函数y=﹣2x2+4x+1的图象，然后通过观察抛物线与x轴的交点，该同学得出﹣1＜x1＜0，2＜x2＜3的结论，该同学采用的方法体现的数学思想是（ ） A．类比 B．演绎 C．数形结合 D．公理化 10．如图，在直角坐标系xOy中，△ABC的三个顶点都在方格纸的格点上，点A的坐标是（﹣2，0），将△ABC绕点A顺时针旋 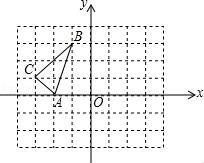转90°得到△AB′C′，则点B的对应点B′的坐标是（ ） A．（1，﹣1） B．（1，1） C．（﹣1，1） D．（﹣1，﹣1） 二、填空题(本大题5小题，每小题3分，共15分) 11．已知点P(2  －a，2a－7)(其中a为整数)位于第三象限，则点P坐标为________ ．12．如图4×5的方格纸中，在除阴影之外的方格中任意选择一个涂黑，与图中阴影部分构成轴对称图形的涂法有______种．  13．某自然保护区的工作人员，欲估算该自然保护区栖息的某种鸟类的数量．他们首先随机捕捉了500只这种鸟，做了标记之后将其放回，经过一段时间之后，他们又从该保护区随机捕捉该种鸟300只，发现其中20只有之前做的标记，则该保护区有这种鸟类大约______只 14．如图，为一块面积为1.5m2的直角三角形模板，其中∠B=90°，AB=1.5m，现要把它加工成正方形DEFG木板（EF在AC上，点D和点G分别在AB和BC上），则该正方形木板的边长为______m．  15．如图，在平面直角坐标系xOy中，菱形OABC的顶点A在x轴上，顶点B的坐标为（8，4），点P是对角线OB上一个动点，点D的坐标为（0，﹣2），当DP与AP之和最小时，点P的坐标为______．  三、解答题(本大题共8小题，共75分) 16．(本题共2小题，每小题5分，共10分) (1)计算：(－)－1－|－3|－(3－π)0＋2cos45°. (2)分解因式：(x2－x)2－12(x2－x)＋36. 17．如图，已知⊙O和⊙O上的一点A，请完成下列任务： （1）作⊙O的内接正六边形ABCDEF； （2）连接BF，CE，判断四边形 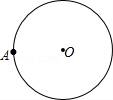BCEF的形状并加以证明． 18．为践行社会主义核心价值观，某市教育局准备举办教室“敬业杯”课堂教学技能大赛，参赛选手均由  辖区内各个学校选派，某校首先在校内组织部分教师进行了预赛，并将预赛成 绩绘制成了如下不完整的统计图表，请根据图表回答下列问题：
（1）表格中a的值为______，扇形统计图中，表示类别③的扇形的圆心角度数为______度； （2）该校决定从预赛中获得优秀等级的三名教师中随机选取两名参加市教育局举办的课堂教学技能大赛，已知三名教师中有两名男教师、一名女教师，请用树状图或列表法说明该校选中一男一女教师参加市教育局举办的课堂教学技能大赛的概率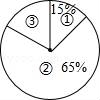．  19．如图，在平面直角坐标系xOy中，一次函数y=k1x+b与反比例函数y=  的图象交于点A（﹣1，6）和点B（3，m），与y轴交于点C，与x轴交于点D．（1）求一次函数y=k1x+b和反比例函数y=   的表达式；（2）点P是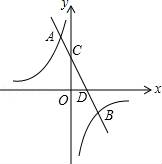双曲线y= 上的一点，且满足S△PCD=S△DOE，求点P的坐标． 20．(本题8分)某校准备组织学生及家长代表到桂林进行社会实践活动，为便于管理，所有人员必须乘坐同一列高铁，高铁单程票价格如表所示，二等座学生票可打7.5折，已知所有人员都买一等座单程火车票需6175元，都买二等座单程火车票需3150元；如果家长代表与教师的人数之比为2∶1.
(1)参加社会实践活动的老师、家长代表与学生各有多少人？ (2)由于各种原因，二等座单程火车票只能买x张(x＜参加社会实践的总人数)，其余的须买一等座单程火车票，在保证所有人员都有座位的前提下，请你设计最经济的购票方案，并写出购买单程火车票的总费用y与x之间的函数关系式； (3)在  (2)的方案下，请求出当x＝30时，购买单程火车票的总费用．21．(本题10分)放风筝是大家喜爱的一种运动，星期天的上午小明在市政府广场上放风筝．如图，他在A处不小心让风筝挂在了一棵树梢上，风筝固定在了D处，此时风筝AD与水平线的夹角为30°，为了便于观察，小明迅速向前边移动，收线到达了离A处10米的B处，此时风筝线BD与水平线的夹角为45°.已知点A，B，C在同一条水平直线上，请你求出小明此时所收回的风筝线的长度是多少米？(风筝线AD，BD均为线段，≈1.414，≈1.732，最后结果精确到1米)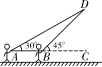．  22．如 图1，在△ABC和△MNB中，∠ACB=∠MBN=90°，AC=BC=4，MB=NB=2，点N在BC边上，连接AN，CM，点E，F，D，G分别为AC，AN，MN，CM的中点，连接EF，FD，DG，EG．（1）判断四边形EFDG的形状，并证明； （2）求FD的长； （3）如图2，将图1中的△MBN绕点B逆时针旋转90°，其他条件不变，猜想此时四边形EFDG的形状，并证明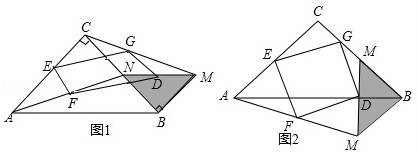．  23．(本题14分)如图，抛物线y＝ax2＋bx过A(4，0)，B(1，3)两点，点C、B关于抛物线的对称轴对称，过点B作直线BH  ⊥x轴，交x轴于点H.(1)求抛物线的表达式，并求出△ABC的面积； (2)点P是抛物线上一动点，且 位于第四象限，当△ABP的面积为6时，求出点P的坐标；(3)若点M在直线BH上运动，点N在x轴上运动，当以点C、M、N为顶点的三角形为等腰直角三角形时，请直接写出此时△CMN的面积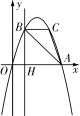．  (责任编辑：admin) |