|
☆☆☆ 点击下载试题 ☆☆☆ 由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看! 本试卷共三大题25小题,总分150分,考试时间120分钟。考生务必填写清楚姓名。将答案填写在试卷上,考试结束后上交。 第Ⅰ卷水平测试(100分) 1、选择题(每题5分,共30分。每题仅有一个正确选项) 1. 下列事件中,是必然发生事件的是 ( ) A 通常情况下,抛出的篮球会下落 B 抛一枚质地均匀的骰子,朝上一面的点数是3 C 阴天一定会下雪 D 抛两枚均匀的硬币,落地后,都是正面朝上 2. 下列汽车标志中,既是轴对称图形又是中心对称图形的是( )  3. 将抛物线 A. 4. 广州市白云山风景区自然风景优美,是国家五A景区,每天吸引大量游客前来游览,经统计,今年重阳节当天来白云山风景区游览的人数约为36000人,用科学计数法表示36000为 ( ) A. 5. 要使分式 A. 1或-2 B. -2 C. 1 D.-1 6. 在同一直角坐标系中,二次函数y=x2+2与一次函数y=2x的图象大致是 A.  B. B.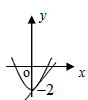 C. C.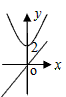 D. D.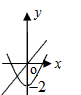 7.若正六边形的半径长为4,则它的边长等于 ( ) A.4 B. 2 C. 8.若5k+20<0,则关于x的一元二次方程x2+4x﹣k=0的根的情况是( ) A没有实数根 B有两个相等的实数根 C 有两个不相等的实数根 D无法判断 9. 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( ) A.π B. 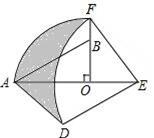 10. 如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( ) 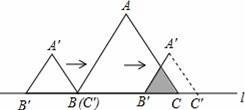 A. 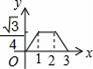 B. B.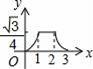 C. C.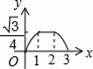 D. D.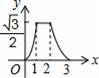 二、填空题(每题3分,共18分。每题仅有一个正确选项) 11.在校田径运动会上,小明和其他三名选手参加100米预赛,赛场共设1,2,3,4四条跑道,选手以随机抽签的方式决定各自的跑道,若小明首先抽签,则小明抽到1号跑道的概率是__________ 12.二次函数 13.如图,将△ABC绕点A逆时针旋转的到△ADE,点C和点E是对应点,若∠CAE=90 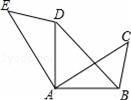 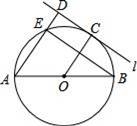 第13题 第15题 14.若圆锥的底面圆的周长为8π,侧面展开图的圆心角为90°,则该圆锥的母线长为___________ 15.如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为 . 16.若关于x的方程 三、解答题(本小题有9个小题,共102分,解答要求写出文字说明,证明过程或计算过程) 17.(本题满分9分)解方程 (1) 18.(本题满分9分) 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(项点是网格线的交点). 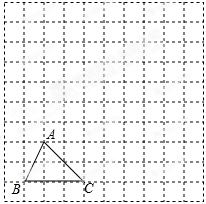 (1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,请画出△A1B1C1; (2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2; (3)线段B1C1变换到B1C2的过程中扫过区域的面积为 . 19. (本题满分10分) 已知二次函数 (1)用配方法配成顶点式 (2)求出二次函数与x轴的两个交点坐标A,B(A在B的左侧) (3)把函数沿x轴向右平移两个单位,在把函数沿y轴向上平移3个单位,求出平移后的函数图像。
如图,在△ABC中, (1)判断直线DE与圆O的位置关系,并说明理由 (2)若AC=6,BC=8,OA=2,求线段DE的长 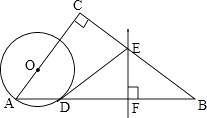 21. (本题满分12分) 为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有4各不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目. (1)请用树形图法或列表法,表示某个同学抽签的各种可能情况. (2)小张同学对物理的①、②和化学的b、c号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少? 22. (本题满分12分) 如图,平行四边形ABCD中,AB⊥AC,AB=1,BC= (1)证明:当旋转角为90°时,四边形ABEF是平行四边形; (2)试说明在旋转过程中,线段AF与EC总保持相等; (3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数. 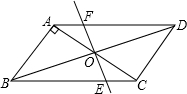
某商业公司为指导某种应季商品的生产和销售,对三月份至七月份该商品的售价和成本进行了调研,结果如下:每件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图1),每件商品的成本Q(元)与时间t(月)的关系可用一条抛物线的一部分上的点来表示(如图2)。 (说明:图1,图2中的每个实心黑点所对应的纵坐标分别指相应月份的售价和成本.) 请你根据图象提供的信息回答: (1)每件商品在3月份出售时的利润(利润=售价﹣成本)是多少元? (2)求图2中表示的每件商品的成本Q(元)与时间t(月)之间的函数关系式(不要求写自变量的取值范围); (3)你能求出三月份至七月份每件商品的利润W(元)与时间t(月)之间的函数关系式吗(请写出计算过程,不要求写自变量的取值范围)?若该公司共有此种商品30000件,准备在一个月内全部售完,请你计算一下至少可获利多少元? 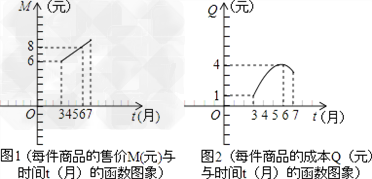 24. (本题满分14分) 如图,已知⊙O上依次有A,B,C,D四个点, (1)若⊙O的半径为3,∠DAB=120°,求劣弧 (2)求证:BF= (3)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系 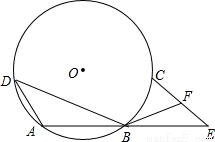 25. (本题满分14分) 如图1,抛物线y=ax2+b的顶点坐标为(0,﹣1),且经过点A(﹣2,0). 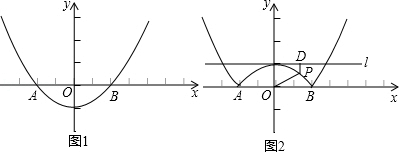 (1)求抛物线的解析式; (2)若将抛物线y=ax2+b中在x轴下方的图象沿x轴翻折到x轴上方,x轴上方的图象保持不变,就得到了函数y=|ax2+b|图象上的任意一点,直线l是经过(0,1)且平行与x轴的直线,过点P作直线l的垂线,垂足为D,猜想并探究:PO与PD的差是否为定值?如果是,请求出此定值;如果不是,请说明理由. (责任编辑:admin) |
