|
☆☆☆ 点击下载试题 ☆☆☆ 2018晋城中考数学冲刺压轴试题【最新Word版含答案】 由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ 一、选择题（本大题共10个小题，每小题3分，共30分． 1．（3分）计算﹣1+2的结果是（ ） A．﹣3 B．﹣1 C．1 D．3 2．（3分）如图，直线a，b被直线c所截，下列条件不能判定直线a与b平行的是（ ）  A．∠1=∠3 B．∠2+∠4=180° C．∠1=∠4 D．∠3=∠4 3．（3分）在体育课上，甲、乙两名同学分别进行了5次跳远测试，经计算他们的平均成绩相同．若要比较这两名同学的成绩哪一个更为稳定，通常需要比较他们成绩的（ ） A．众数 B．平均数 C．中位数 D．方差 4．（3分）将不等式组  的解集表示在数轴上，下面表示正确的是（ ）A．  B C． D． 5．（3分）下列运算错误的是（ ） A．（  ﹣1）0=1 B．（﹣3）2÷ = C．5x2﹣6x2 =﹣x2 D．（2m3）2÷（2m）2=m46．（3分）如图，将矩形纸片ABCD沿BD折叠，得到△BC′D，C′D与AB交于点E．若∠1=35°，则∠2的度数为（ ）  A．20° B．30° C．35° D．55° 7．（3分）化简  ﹣ 的结果是（ ）A．﹣x2+2x B．﹣x2+6x C．﹣  D．8．（3分）2017年5月18日，我国宣布在南海神狐海域成功试采可燃冰，成为世界上首个在海域连续稳定产气的国家．据粗略估计，仅南海北部陆坡的可燃冰资源就达到186亿吨油当量，达到我国陆上石油资源总量的50%．数据186亿吨用科学记数法可表示为（ ）  A．186×108吨 B．18.6×109吨 C．1.86×1010吨 D．0.186×1011吨 9．（3分）公元前5世纪，毕达哥拉斯学派中的一名成员希伯索斯发现了无理数  ，导致了第一次数学危机， 是无理数的证明如下：假设 是有理数，那么它可以表示成 （p与q是互质的两个正整数）．于是（）2=（ ）2=2，所以，q2=2p2．于是q2是偶数，进而q是偶数，从而可设q=2m，所以（2m）2=2p2，p2=2m2，于是可得p也是偶数．这与“p与q是互质的两个正整数”矛盾．从而可知“是有理数”的假设不成立，所以，是无理数．这种证明“ 是无理数”的方法是（ ）A．综合法 B．反证法 C．举反例法 D．数学归纳法 10．（3分）如图是某商品的标志图案，AC与BD是⊙O的两条直径，首尾顺次连接点A，B，C，D，得到四边形ABCD．若AC=10cm，∠BAC=36°，则图中阴影部分的面积为（ ）  A．5πcm2 B．10πcm2 C．15πcm2 D．20πcm2 二、填空题（本大题共5个小题，每小题3分，共15分） 11．（3分）计算：4  ﹣9 = ．12．（3分）某商店经销一种品牌的洗衣机，其中某一型号的洗衣机每台进价为a元，商店将进价提高20%后作为零售价进行销售，一段时间后，商店又以9折优惠价促销，这时该型号洗衣机的零售价为 元．  13．（3分）如图，已知△ABC三个顶点的坐标分别为A（0，4），B（﹣1，1），C（﹣2，2），将△ABC向右平移4个单位，得到△A′B′C′，点A，B，C的对应点分别为A′、B′、C′，再将△A′B′C′绕点B′顺时针旋转90  °，得到△A″B″C″，点A′、B′、C′的对应点分别为A″、B″、C″，则点A″的坐标为 ． 14．（3分）把直线y=3x向下平移2个单位后所得到直线的解析式为y= ． 15．（3分）如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点P是AB上的任意一点，作PD⊥AC于点D，PE⊥CB于点E，连结DE，则DE的最小值为 ．  三、解答题（本大题共5个小题，共55分．解答应写出文字说明、证明过程或演算步骤） 16．（10分）（1）解方程：  ．（2）分解因式：（y+2x）2﹣（x+2y）2． 17．（6分）已知：如图，在▱ABCD中，延长AB至点E，延长CD至点F，使得BE=DF．连接EF，与对角线AC交于点O． 求证：OE=OF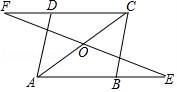．  18．（10分）如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，其边长为2，点A，点C分别在x轴，y轴的正半轴上，函数y=2x的图象与CB交于点D，函数y=  （k为常数，k≠0）的图象经过点D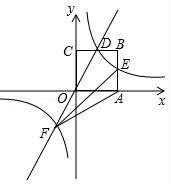，与AB交于点E，与函数y=2x的图象在第三象限内交于点F，连接AF、EF．（1）求函数y= 的表达式，并直接写出E、F两点的坐标；（2）求△AEF的面积．  19．（10分）“春种一粒粟，秋收万颗子”，唐 代诗人李绅这句诗中的“粟”即谷子（去皮后则称为“小米”），被誉为中华民族的哺育作物．我省有着“小杂粮王国”的美誉，谷子作为我省杂粮谷物中的大类，其种植面积已连续三年全国第一．2016年全国谷子种植面积为2000万亩，年总产量为150万吨，我省谷子平均亩产量为160kg，国内其他地区谷子的平均亩产量为60kg，请解答下列问题：（1）求我省2016年谷子的种植面积是多少万亩． （2）2017年，若我省谷子的平均亩产量仍保持160kg不变，要使我省谷子的年总产量不低于52万吨，那么，今年我省至少应再多种植多少万亩的谷子？  20．（19分）综合与实践 背景阅读 早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于我  国古代著名数学著作《周髀算经》中，为了方便，在本题中，我们把三边的比为3：4：5的三角形称为（3，4，5）型三角形，例如：三边长分别为9，12，15或3 ，4，5的三角形就是（3，4，5）型三角形，用矩形纸片按下面的操作方法可以折出这种类型的三角形．实践操作 如图1，在矩形纸片ABCD中，AD=8cm，AB=12cm． 第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平． 第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF． 第三步：如图4，将图3中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF交于点N，然后展平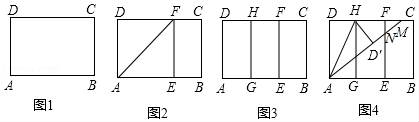．  问题解决 （1）请在图2中证明四边形AEFD是正方形． （2）请在图4中判断NF与ND′的数量关系，并加以证明； （3）请在图4中证明△AEN（3，4，5）型三角形； 探索发现 （4）在不添加字母的情况下，图4中还有哪些三角形是（3，4，5）型三角形？请找出并直接写出它们的名称． 2018晋城中考数学冲刺压轴试题参考答案与试题解析 一、选择题（本大题共10个小题，每小题3分，共30分． 1．（3分）计算﹣1+2的结果是（ ） A．﹣3 B．﹣1 C．1 D．3 【解答】解：﹣1+2=1． 故选：C． 2．（3分）如图，直线a，b被直线c所截，下列条件不能判定直线a与b平行的是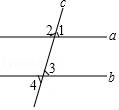（ ）  A．∠1=∠3 B．∠2+∠4=180° C．∠1=∠4 D．∠3=∠4 【解答】解：由∠1=∠3，可得直线a与b平行，故A能判定； 由∠2+∠4=180°，∠2=∠5，∠ 4=∠3，可得∠3+∠5=180°，故直线a与b平行，故B能判定；由∠1=∠4，∠4=∠3，可得∠1=∠3，故直线a与b平行，故C能判定； 由∠3=∠4，不能判定直线a与b平行， 故选：D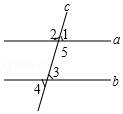．  3．（3分）在体育课上，甲、乙两名同学分别进行了5次跳远测试，经计算他们的平均成绩相同．若要比较这两名同学的成绩哪一个更为稳定，通常需要比较他们成绩的（ ） A．众数 B．平均数 C．中位数 D．方差 【解答】解：因为方差是反映一组数据的波动大小的一个量．方差越大，则各数据与其平均值的离散程度越大，稳定性也越小；反之，则各数据与其平均值的离散程度越小，稳定性越好；所以要比较这两名同学的成绩哪一个更为稳定，通常需要比较他们成绩的方差． 故选：D． 4．（3分）将不等式组  的解集表示在数轴上，下面表示正确的是（ ）A．  B． C． D． 【解答】解：  解不等式①得，x≤3 解不等式②得，x＞﹣4 在数轴上表示为：  故选：A． 5．（3分）下列运算错误的是（ ） A．（ ﹣1）0=1 B．（﹣3）2÷= C．5x2﹣6x2=﹣x2 D．（2m3）2÷（2m）2=m4【解答】解：A、（ ﹣1）0=1，正确，不符合题意；B、（﹣3）2÷  =4，错误，符合题意；C、5x2﹣6x2=﹣x2，正确，不符合题意； D、（2m3）2÷（2m）2=m4，正确，不符合题意； 故选：B． 6．（3分）如图，将矩形纸片ABCD沿BD折叠，得到△BC′D，C′D与AB交于点E．若∠1=35°，则∠2的度数为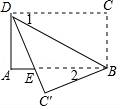（ ）  A．20° B．30° C．35° D．55° 【解答】解：∵∠1=35°，CD∥AB， ∴∠ABD=35°，∠DBC=55°， 由折叠可得∠DBC'=∠DBC=55°， ∴∠2=∠DBC'﹣∠DBA=  55°﹣35°=20°，故选：A． 7．（3分）化简  ﹣ 的结果是（ ）A．﹣x2+2x B．﹣x2+6x C．﹣  D． 【解答】解：原式=  ﹣ =  =﹣ 故选：C． 8．（3分）2017年5月18日，我国宣布在南海神狐海域成功试采可燃冰，成为世界上首个在海域连续稳定产气的国家．据粗略估计，仅南海北部陆坡的可燃冰资源就达到186亿吨油当量，达到我国陆上石油资源总量的50%．数据186亿吨用科学记数法可表示为（ ）  A．186×108吨 B．18.6×109吨 C．1.86×1010吨 D．0.186×1011吨 【解答】解：186亿吨=1.86×1010吨． 故选：C． 9．（3分）公元前5世纪，毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 ，导致了第一次数学危机，是无理数的证明如下：假设 是有理数，那么它可以表示成 （p与q是互质的两个正整数）．于是（）2=（）2=2，所以，q2=2p2．于是q2是偶数，进而q是偶数，从而可设q=2m，所以（2m）2=2p2，p2=2m2，于是可得p也是偶数．这与“p与q是互质的两个正整数”矛盾．从而可知“是有理数”的假设不成立，所以，是无理数．这种证明“ 是无理数”的方法是（ ）A．综合法 B．反证法 C．举反例法 D．数学归纳法 【解答】解：由题意可得：这种证明“ 是无理数”的方法是反证法．故选：B． 10．（3分）如图是某商品的标志图案，AC与BD是⊙O的两条直径，首尾顺次连接点A，B，C，D，得到四边形ABCD．若AC=10cm，∠BAC=36°，则图中阴影部分的面积为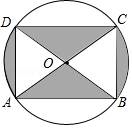（ ）  A．5πcm2 B．10πcm2 C．15πcm2 D．20πcm2 【解答】解：∵AC与BD是⊙O的两条直径， ∴∠ABC=∠ADC=∠DAB=∠BCD=90°， ∴四边形ABCD是矩形， ∴△ABO与△CDO的面积的和=△AOD与△BOC的面积的和， ∴图中阴影部分的面积=S扇形AOD+S扇形BOC=2S扇形AOD， ∵OA=OB， ∴∠BAC=∠ABO=36°， ∴∠AOD=72°， ∴图中阴影部分的面积=2×  =10π，故选：B． 二、填空题（本大题共5个小题，每小题3分，共15分） 11．（3分）计算：4  ﹣9 = 3 ．【解答】解：原式=12  =3，故答案为：3 ． 12．（3分）某商店经销一种品牌的洗衣机， 其中某一型号的 洗衣机每台进价为a元，商店将进价提高20%后作为零售价进行销售，一段时间后，商店又以9折优惠价促销，这时该型号洗衣机的零售价为 1.08a 元． 【解答】解：由题意可得， 该型号洗衣机的零售价为：a（1+20%）×0.9=1.08a（元）， 故答案为：1.08a． 13．（3分）如图，已知△ABC三个顶点的坐标分别为A（0，4），B（﹣1，1），C（﹣2，2），将△ABC向右平移4个单位，得到△A′B′C′，点A，B，C的对应点分别为A′、B′、C′，再将△A′B′C′绕点B′顺时针旋转90°，得到△A″B″C″，点A′、B′、C′的对应点分别为A″、B″、C″，则点A″的坐标为 （6，0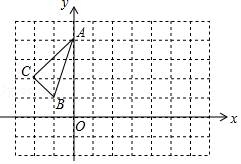） ．  【解答】解：如图所示： ∵A（0，4），B（﹣1，1），C（﹣2，2），将△ABC向右平移4个单位，得到△A′B′C′， ∴A′、B′、C′的坐标分别为（4，4），B（3，1），C（2，2）， 再将△A′B′C′绕点B′顺时针旋转90°，得到△A″B″C″， 则点A″的坐标为 （6，0）； 故答案为：（6，0）．  14．（3分）把直线y=3x向下平移2个单位后所得到直线的解析式为y= 3x﹣2 ． 【解答】解：把直线y=3x向下平移2个单位后所得到直线的解析式为y=3x﹣2． 故答案为3x﹣2． 15．（3分）如图，在Rt△ABC中 ，∠C=90°，AC=8，BC=6，点P是AB上的任意一点，作PD⊥AC于点D，PE⊥CB于点E，连结DE，则DE的最小值为 4.8 ． 【解答】解：∵Rt△ABC中，∠C=90°，AC=8，BC=6， ∴AB=10， 连接CP， ∵PD⊥AC于点D，PE⊥CB于点E， ∴四边形DPEC是矩形， ∴DE=CP， 当DE最小时，则CP最小，根据垂线段最短可知当CP⊥AB时，则CP最小， ∴DE=CP=  =4.8，故答案为：4.8．  三、解答题（本大题共5个小题，共55分．解答应写出文字说明、证明过程或演算步骤） 16．（10分）（1）解方程：  ．（2）分解因式：（y+2x）2﹣（x+2y）2． 【解答】解：（1）方程两边同时×（x﹣1），得：2x﹣3=x﹣1， 移项、合并同类项，得：x=2， 经检验，x=2是原分式方程的解，且符合题意，∴原分式方程的解为：x=2． （2）原式=[（y+2x）+（x+2y）][（y+2x）﹣（x+2y）]， =（2x+y+x+2y）（2x +y﹣x﹣2y），=（3x+3y）（x﹣y）， =3（x+y）（x﹣y）， =3x2﹣3y2． 17．（6分）已知：如图，在▱ABCD中 ，延长AB至点E，延长CD至点F，使得BE=DF．连接EF，与对角线AC交于点O．求证：OE=OF．  【解答】证明：∵四边形ABCD是平行四边形， ∴AB∥CD，AB=CD， ∵BE=DF， ∴AB+BE=CD+DF，即AE=CF， ∵AB∥CD， ∴AE∥CF， ∴∠E=∠F，∠OAE=∠OCF， 在△AOE和△COF中，  ，∴△AOE≌△COF（ASA）， ∴OE=OF． 18．（10分）如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，其边长为2，点A，点C分别在x轴，y轴的正半轴上，函数y=2x的图象与CB交于点D，函数y= （k为常数，k≠0）的图象经过点D，与AB交于点E，与函数y=2x的图象在第三象限内交于点F，连接AF、EF．（1）求函数y= 的表达式，并直接写出E、F两点的坐标；（2）求△AEF的面积． 【解答】解：（1）∵正方形OABC的边长为2， ∴点D的纵坐标为2，即y=2， 将y=2代入y=2x，得x=1， ∴点D的坐标为（1，2）， ∵函数y= 的图象经过点D，∴2=  ，解得k=2， ∴函数y=  的表达式为y= ，∴E（2，1），F（﹣1，﹣2）； （2）过点F作FG⊥AB，与BA的延长线交于点G， （3）∵E（2，1），F（﹣1，﹣2）， ∴AE=1， FG=2﹣（﹣1）=3， ∴△AEF的面积为：  AE•FG=×1×3= ． 19．（10分）“春种一粒粟，秋收万颗子”，唐代诗人李绅这句诗中的“粟”即谷子（去皮后则称为“小米”），被誉为中华民族的哺育作物．我省有着“小杂粮王国”的美誉，谷子作为我省杂粮谷物中的大类，其种植面积已连续三年全国第一．2016年全国谷子种植面积为2000万亩，年总产量为150万吨，我省谷子平均亩产量为160kg，国内其他地区谷子的平均亩产量为60kg，请解答下列问题： （1）求我省2016年谷子的种植面积 是多少万亩．（2）2017年，若我省谷子的平均亩产量仍保持160kg不变，要使我省谷子的年总产量不低于52万吨，那么，今年我省至少应再多种植多少万亩的谷子？ 【解答】解：（1）设我省2016年谷子的种植面积是x万亩，其他地区谷子的种植面积是y万亩，依题意有  ，解得  ．答：我省2016年谷子的种植面积是300万亩． （2）设我省应种植z万亩的谷子，依题意有  ，解得z≥325， 325﹣300=25（万亩）． 答：今年我省至少应再多种植25万亩的谷子． 20．（19分）综合与实践 背景阅读 早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于我国古代著名数学著作《周髀算经》中，为了方便，在本题中，我们把三边的比为3：4：5的三角形称为（3，4，5）型三角形，例如：三边长分别为9，12，15或3 ，4，5的三角形就是（3，4，5）型三角形，用矩形纸片按下面的操作方法可以折出这种类型的三角形．实践操作 如图1，在矩形纸片ABCD中，AD=8cm，AB=12cm． 第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平． 第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF． 第三步：如图4，将图3中的 矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF交于点N，然后展平．问题解决 （1）请在图2中证明四边形AEFD是正方形． （2）请在图4中判断NF与ND′的数量关系，并加以证明； （3）请在图4中证明△AEN（3，4，5）型三角形； 探索发现 （4）在不添加字母的情况下，图4中还有哪些三角形是（3，4，5）型三角形？请找出并直接写出它们的名称． 【解答】（1）证明：∵四边形ABCD是矩形， ∴∠D=∠DAE=90°， 由折叠的性质得，AE=AD，∠AEF=∠D=90°， ∴∠D=∠DAE=∠AEF=90°， ∴四边形AEFD是矩形， ∵AE=AD， ∴矩形AEFD是正方形； （2）解：NF=ND′， 理由：连接HN，由折叠得，∠AD′H=∠D=90°，HF=HD=HD′， ∵四边形AEFD是正方形， ∴∠EFD=90°， ∵∠AD′H=90°， ∴∠HD′N=90°， 在Rt△HNF与Rt△HND′中，  ，∴Rt△HNF≌Rt△HND′， ∴NF=ND′； （3）解：∵四边形AEFD是正方形， ∴AE=EF=AD=8cm， 由折叠得，AD′=AD=8cm， 设NF=xcm，则ND′= xcm，在Rt△AEN中， ∵AN2=AE2+EN2， ∴（8+x）2=82+（8﹣x）2， 解得：x=2， ∴AN=8+x=10cm，EN=6cm， ∴EN：AE：AN=3：4：5， ∴△AEN是（3，4，5）型三角形； （4）解：图4中还有△MFN，△MD′H，△MDA是（3，4，5）型三角形， ∵CF∥AE， ∴△MFN∽△AEN， ∵EN：AE：AN=3：4：5， ∴FN：MF：CN=3：4：5， ∴△MFN是（3，4，5）型三角形； 同理，△MD′H，△MDA是（3，4，5）型三角形．  (责任编辑：admin) |