|
☆☆☆ 点击下载试题 ☆☆☆  2018年衡水市中考数学模拟试卷【精编Word版】 由于格式问题可能会出现乱码的情况，请点击右上角全屏查看 一、选择题（本大题有16个小题，共42分） 1．（3分）计算4﹣2的结果是（ ） A．﹣8 B．﹣  C．﹣ D．2．（3分）若方程  =1有增根，则它的增根是（ ）A．0 B．1 C．﹣1 D．1和﹣1 3．（3分）超级磁力风力发电机可以大幅度提升风力发电效率，但其造价高昂，每座磁力风力发电机，其建造花费估计要5 300万美元，“5 300万”用科学记数法可表示为（ ） A．5.3×103 B．5.3×104 C．5.3×107 D．5.3×108 4．（3分）如图，已知正五边形ABCDE，AF∥CD，交DB的延长线于点F，则 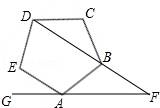 ∠DFA等于（ ） A．30° B．36° C．45° D．32° 5．（3分）多项式4x2﹣4与多项式x2﹣2x+1的公因式是（ ） A．x﹣1 B．x+1 C．x2﹣1 D．（x﹣1）2 6．（3分）如图，正方形OEFG和正方形ABCD是位似图形，且点F与点C是一对对应点，点F的坐标是（1，1），点C的坐标是（4，2）；则它们的位似中心的坐标是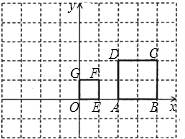（ ）  A．（0，0） B．（﹣1，0） C．（﹣2，0） D．（﹣3，0） 7．（3分）学校广播站要招聘1名记者，小明、小亮和小丽报名参加了3项素质测试，成绩如下：
现在要计算3人的加权平均分，如果将采访写作、计算机和创意设计这三项的权重比由3：5：2变成5：3：2，成绩变化情况是 （ ） A．小明增加最多 B．小亮增加最多 C．小丽增加最多 D．三人的成绩都增加 8．（3分）如图，四边形纸片ABCD中，∠A=70°，∠B=80°，将纸片折叠，使C，D落在AB边上的C′，D′处，折痕为MN，则∠AMD′+∠BNC′=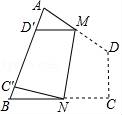（ ）  A．50° B．60° C．70° D．80° 9．（3分）某初中毕业班的每一个同学都将自己的相片向全班其他同学各送一张表示留念，全班共送了2550张相片，如果全班有x名学生，根据题意，列出方程为（ ） A．x（x+1）=2550 B．x（x﹣1）=2550 C．2x（x+1）=2550 D．x（x﹣1）=2550×2 10．（2分）下列命题： ①若a+b+c=0，则b2﹣4ac≥0；②若b=2a+3c，则一元二次方程ax2+bx+c=0有两个不相等的实数根；③若b2﹣4ac＞0，则二次函数的图象与坐标轴的公共点的个数是2或3．其中正确的是（ ） A．①② B．①③ C．②③ D．①②③ 11．（2分）如图①，在边长为2cm的正方形ABCD中，点P以每秒1cm的速度从点A出发，沿AB→BC的路径运动，到点C停止，过点P作PQ∥BD，PQ与边AD（或边CD）交于点Q，PQ的长度y（cm）与点P的运动时间x（秒）的函数图象如图②所示．当点P运动3秒时，PQ的长是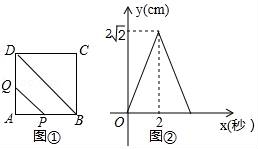（  ） A．  cm B． cm C． cm D． cm12．（2分）如图，四个有理数在数轴上的对应点分别为M，P，N，Q，若原点在点N与点P之间，则绝对值最大的数表示的点是（ ）  A．点M B．点P C．点Q D．点N 13．（2分）如图，已知  在△ABC中，点D、E分别在边AB、AC上，DE∥BC，AD：BD=2：1，点F在AC上，AF：FC=1：2，联结BF，交DE于点G，那么DG：GE等于（ ） A．1：2  B．1：3 C．2：3 D．2：5．14．（2分）给出三个命题：①点P（b，a）在抛物线y=x2+1上；②点A（1，3）能在抛物线y=ax2+bx+1上；③点B（﹣2，1）能在抛物线y=ax2﹣bx+1上．若①为真命  题，则（ ）A．②③都是真命题 B．②③都是假命题 C．②是真命题，③是假命题 D．②是假命题，③是真命题 15．（2分）如图，△ABC中，D、E是BC边上的点，BD：DE：EC=3：2：1，M在AC边上，CM：MA=1：2，BM交AD，AE于H，G，则BH：HG：GM等于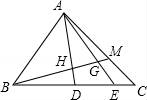（ ）  A．3：2：1 B．5：3：1 C．25：12：5 D．51：24：10 二、填空题（本大题有3个小题，共10分）  16．（3分）在（  ）0，|﹣ |，tan30°，10﹣2这几个实数中，最大的实数是 ．17．（3分）比较大小：  ﹣3 cos45°（填“＞”“=”或“＜”）．18.如图，PA切⊙O于A，OP交⊙O于B，且PB=1，PA= 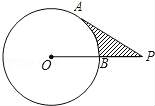 ，则阴影部分的面积：S= ． 19．（3分）如图，矩形ABCD中，BC=2，DC=4，以AB为直径的半圆O与DC相切于点E，则阴影部分的面积为 ．（结果保留π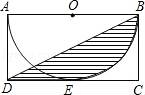）  20．（4分）如图，梯形AOBC的顶点A，C在反比例函数图象上，OA∥BC，上底边OA在直线y=x上，下底边BC交y轴于B（0，﹣4），则四边形AOBC的面积为 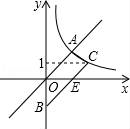．  三、解答题（本大题有7个小题，共68分） 19．（9分）如图，在直角坐标  系中，先描出点A（1，3），点B（4，1）（1）用尺规在x轴上找一点C，使AC+BC的值最小（保留作图痕迹）； （2）用尺规在x轴上找一点P，使PA=PB（保留作图痕迹）．  20．（9分）已知分式（  +n）÷ ，然后解答下列问题．（1）若n满足一元二次方程n2+n﹣2=0，先化简原分式，再求值； （2）原分式的值能等于0吗？为什么？ 21．（9分）建立模型： （1）如图 1，已知△ABC，AC=BC，∠C=90°，顶点C在直线 l 上．操作：过点A作AD⊥l于点D，过点B作BE ⊥l于点E，求证△CAD≌△BCE．模型应用： （2）如图2，在直角坐标系中，直线l1：y=  x+8与y轴交于点A，与x轴交于点B，将直线l1绕着点A顺时针旋转45°得到l2． 求l2的函数表达式．（3）如图3，在直角坐标系中，点B（10，8），作BA⊥y轴于点 A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，2a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．  22． （9分）在一节数学活动课上，王老师将本班学生身高数据（精确到1厘米）出示给大家，要求同学们各自独立绘制一幅频数分布直方图，甲绘制的如图①所示，乙绘制的如图②所示，经王老师批改，甲绘制的图是正确的，乙在数据整理与绘图过程中均有个别错误．（1）写出乙同学在数据整理或绘图过程中的错误（写出一个即可）；  （2）甲同学在数据整理后若用扇形统计图表示，则159.5﹣164.5这一部分所  对应的扇形圆心角的度数为 ；（3）该班学生的身高数据的中位数是 ； （4）假设身高在169.5﹣174.5范围的5名同学中，有2名女同学，班主任老师想在这5名同学中选出2名同学作为本班的正、副旗手，那么恰好选中一名男同学和一名女同学当正，副旗手的概率是多少？ 23．（10分）如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足  = ，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．（1）求证：△ADF∽△AED； （2）求FG的长； （3）求证：tan∠E=  ． 24．（10分）已知关于x的二次函数y=﹣x2﹣2x﹣  与x轴有两个交点，m为正整数．（1）当﹣x2﹣2x﹣ =0时，求m的值；（2）如图，当该二次函数的图象经过原点时，与直线y=﹣x﹣2的图象交于A，B两点，求A，B两点的坐标； （3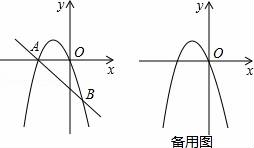）  将（2）中的二次函数图象x轴上方的部分沿x轴翻折到x轴下方，图象的 其余部分保持不变，翻折后的图象与原图象x轴下方的部分组成一个“M”形状的新图象．现有直线y=a（a≠0）与该新图象恰好有两个公共点，直接写出a的取值范围． (责任编辑：admin) |