|
☆☆☆ 点击下载试题 ☆☆☆  2018泉州市中考数学压轴真题【最新Word版含答案】由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ 一、选择题（每小题4分，共40分） 1．（4分）若代数式  在实数范围内有意义，则x的取值范围是（ ）A．x≥﹣3 B．x＞3 C．x≥3 D．x≤3 2．（4分）方程（m+2）x|m|+3mx+1=0是关于x的一元二次方程，则（ ） A．m=±2 B．m=2 C．m=﹣2 D．m≠±2 3．（4分）下列二次根式中，是最简二次根式的是（ ） A．  B． C． D． 4．（4分）下列计算正确的是（ ） A．  B． C． D． 5．（4分）用配方法解方程x2+4x+1=0，配方后的方程是（ ） A．（x+2）2=3 B．（x﹣2）2=3 C．（x﹣2）2=5 D．（x+2）2=5 6．（4分）如果关于x的一元二次方程x2﹣6x+2k=0有两个实数根，那么实数k的取值范围是（ ） A  ． B． C． D． 7．（4分）已知x=2是方程x2﹣6x+m=0的根，则该方程的另一根为（ ） A．2 B．3 C．4 D．8 8．（4分）已知2＜x＜3，化简：  得（ ）A．1 B．5 C．2x﹣5 D．﹣1 9．（4分）某商品原价168元，经过连续两次降价后的售价为128元，设平均每次降价的百分数为x，则下面所列方程中正确的是（ ） A．168（1+x）2=128 B．168（1﹣x）2=128 C．168（1﹣2x）2=128 D．168（1﹣x2）=128 10．（4分）如图是由三个边长分别为6、9、x的正方形所组成的图形，若直线AB将它分成面积相等的两部分，则x的值是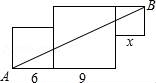（ ）  A．1或9 B．3或5 C．4或  6 D．3或6二、填空题（每小题4分，共24分） 11．（4分）一元二次方程7x﹣3=2x2的一般形式是 ． 12．（4分）方程x2=3x的解为： ． 13．（4分）化简：  = ； = ．14．（4分）计算：  = ； = ．15．（4分） 已知x为实数，且满足（x2+3x）2+x2+3x﹣6=0，那么x2+3x= ．16．（4分）如图，将边长为12的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向向右平移，得到△A′B′C′，当两个三角形重叠部分的面积为32时，它移动的距离AA′等于 ．  三、解答题（9小题，共86分） 17．（14分）计算： （1）  （2）  ．18．（16分）解方程： （1）  （2）x（x﹣2）=4﹣x． 19．（10分）已知关于x的方程x2+ax+a﹣2=0． （1）若该方程的一个根为1，求a的值及该方程的另一根 （2）求证：不论a取何实数，该方程都有两个不相等的实数根． 20．（10分）某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件． （1）填表：
（2）要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品实际售价应定为多少元？ 2 1．（12分）把一边长为40cm的正方形硬纸板，进行适当的剪裁，折成一个长方形盒子（纸板的厚度忽略不计）．如图，若在正方形硬纸板的四角各剪一个同样大小的正方形，将剩余部分折成一个无盖的长方形盒子．（1）要使折成的长方形盒子的底面积为484cm2，那么剪掉的正方形的边长为多少？ （2）折成的长方形盒子的侧面积为600cm2，那么剪掉的正方形的边长为多少？  22．（12分）先阅读下列的解答过程，然后作答： 形如  的化简，只要我们找到两个数a、b使a+b=m，ab=n，这样（ ）2+（ ）2=m， • = ，那么便有 = = ±（a＞b）例如：化简 解：首先把  化为 ，这里m=7，n=12；由于4+3=7，4×3=12，即（  ）2+（ ）2=7， •= ，∴  = = =2+ 由上述例题的方法化简： （1）  ；（2）  ；（3）  ．23．（12分）如图，A、B、C、D为矩形的四个顶点，AB=16cm，AD=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达B为止，点Q以2cm/s的速度向D移动． （1）P、Q两点从出发开始到几秒时，四边形PBCQ的面积为33cm2； （2）P、Q两点从出发开始到几秒时，点P和点Q的距离是10cm．  2018泉州市中考数学压轴真题参考答案 一、选择题（每小题4分，共40分） 1．（4分）若代数式  在实数范围内有意义，则x的取值范围是（ ）A．x≥﹣3 B．x＞3 C．x≥3 D．x≤3 【解答】解：∵代数式 在实数范围内有意义，∴x﹣3≥0， 解得x≥3． 故选：C． 2．（4分）方程（m+2）x|m|+3mx+1=0是关于x的一元二次方程，则（ ） A．m=±2 B．m=2 C．m=﹣2 D．m≠±2 【解答】解：由一元二次方程的定义可得  ，解得：m=2．故选B．3．（4分）下列二次根式中，是最简二次根式的是（ ） A．  B． C． D． 【解答】解：A、  = = ，不是最简二次根式；B、  ，不含有未开尽方的因数或因式，是最简二次根式；C、  = ，被开方数中含有分母，故不是最简二次根式；D、  =2 ，不是最简二次根式．只有选项B中的是最简二次根式，故选B． 4．（4分）下列计算正确的是（ ） A．  B． C． D． 【解答】解：A、  与 不是同类项，不能合并，故本选项错误；B、  •= = ，故本选项正确；C、  =2，故本选项错误；D、  =3，故本选项错误．故选：B． 5．（4分）用配方法解方程x2+4x+1=0，配方后的方程是（ ） A．（x+2）2=3 B．（x﹣2）2=3 C．（x﹣2）2=5 D．（x+2）2=5 【解答】解：方程移项得：x2+4x=﹣1， 配方得：x2+4x+4=3，即（x+2）2=3． 故选：A． 6．（4分）如果关于x的一元二次方程x2﹣6x+2k=0有两个实数根，那么实数k的取值范围是（ ）A．  B． C． D． 【解答】解：∵关于x的一元二次方程x2﹣6x+2k=0有两个实数根， ∴△=（﹣6）2﹣4×1×2k=36﹣8k≥0， 解得：k≤  ．故选：A． 7．（4分）已知x=2是方程x2﹣6x+m=0的根，则该方程的另一根为（ ） A．2 B．3 C．4 D．8 【解答】解：设关于x的方程x2﹣6x+m=0的另一个根是t， 由根与系数的关系得出：t+2=6， 则t=4． 故选：C． 8．（4分）已知2＜x＜3，化简：  得（ ）A．1 B．5 C．2x﹣5 D．﹣1 【解答】解：∵2＜x＜3， ∴ =x﹣2+3﹣x =1． 故选：A． 9．（4分）某商品原价168元，经过连续两次降价后的售价为128元，设平均每次降价的百分数为x，则下面所列方程中正确的是（ ） A．168（1+x）2=128 B．168（1﹣x）2=128 C．168（1﹣2x）2=128 D．168（1﹣x2）=128 【解答】解：第一次降价后的价格为168×（1﹣x），两次连续降价后售价在第一次降价后的价格的基础上降低x， 为168×（1﹣x）×（1﹣x），则列出的方程是168×（1﹣x）2=128． 故选：B． 10．（4分）如图是由三个边长分别为6、9、x的正方形所组成的图形，若直线AB将它分成面积相等的两部分，则x的值是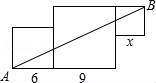（ ）  A．1或9 B．3或5 C．4或6 D．3或6 【解答】解：如图， ∵若直线AB将它分成面积相等的两部分， ∴  （6+9+x）×9﹣x•（9﹣x）= ×（6+9+x）×9﹣6×3，解得x=3，或x=6， 故选：D．  二、填空题（每小题4分，共24分） 11．（4分）一元二次方程7x﹣3=2x2的一般形式是 2x2﹣7x+3=0 ． 【解答】解：一元二次方程7x﹣3=2x2的一般形式是2x2﹣7x+3=0， 故答案是：2x2﹣7x+3=0． 12．（4分）方程x2=3x的解为： x1=0，x2=3 ． 【解答】解：移项得：x2﹣3x=0， 即x（x﹣3）=0， 于是得：x=0或x﹣3=0． 则方程x2=3x的解为：x1=0，x2=3． 故答案是：x1=0，x2=3． 13．（4分）化简：  = 5 ； =  ．【解答】解：原式=5  ；原式=，故答案为：5 ；14．（4分）计算：  = 5 ； =  ．【解答】解：  + =2 +3=5 = = 故答案为：5  ；  15．（4分）已知x为实数，且满足（x2+3x）2+x2+3x﹣6=0，那么x2+3x= ﹣3或2 ． 【解答】解：设t=x2+3x，则原方程转化为关于t的方程t2+t﹣6=0， 整理，得 （t+3）（t﹣2）=0， 解得t=﹣3或t=2． 即x2+3x=﹣3或2． 故答案是：﹣3或2． 16．（4分）如图，将边长为12的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向向右平移，得到△A′B′C′，当两个三角形重叠部分的面积为32时，它移动的距离AA′等于 4或8 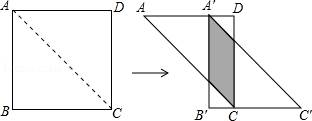．  【解答】解：设AC交A′B′于H， ∵A′H∥CD，AC∥CA′， ∴四边形A′HCD是平行四边形， ∵∠A=45°，∠D=90° ∴△A′HA是等腰直角三角形 设AA′=x，则阴影部分的底长为x，高A′D=12﹣x ∴x•（12﹣x）=32 ∴x=4或8， 即AA′=4或8cm． 故答案为：4或8．  三、解答题（9小题，共86分） 17．（14分）计算： （1）  （2）  ．【解答】解：（1）原式=10  ﹣9+=2 ；（2）原式=3  ﹣（2+2+1）+3﹣1=3  ﹣3﹣2+2= ﹣1．18．（16分  ）解方程：（1）  （2）x（x﹣2）=4﹣x． 【解答】解：（1）  ，（x+3）2=3， x+3=±  ，解得  ；（2）x（x﹣2）=4﹣x， 整理得：x2﹣x﹣4=0， ∵△=1+16=17＞0， ∴x=  ，x1=  ，x2= ．19．（10分）已知关于x的方程x2+ax+a﹣2=0． （1）若该方程的一个根为1，求a的值及该方程的另一根 （2）求证：不论a取何实数，该方程都有两个不相等的实数根． 【解答】（1）解：将x=1代入原方程，得：1+a+a﹣2=0， 解得：a=  ，∴方程的另一根为﹣a﹣1=﹣ ﹣1=﹣ ．答：a的值为   ，方程的另一根为﹣ ．（2）证明：△=a2﹣4（a﹣2）=a2﹣4a+8=（a﹣2）2+4． ∵（a﹣2）2≥0， ∴（a﹣2）2+4＞0，即△＞0， ∴不论a取何实数，该方程都有两个不相等的实数根． 20．（10分）某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件． （1）填表：
（2）要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品实际售价应定为多少元？ 【解答】解：（1）
（2）设要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价x元，由题意，得（360﹣x﹣280）（5x+60）=7200，解得：x1=8，x2=60∵有利于减少库存， ∴x=60． 答：要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价60元． 21．（12分）把一边长为40cm的正方形硬纸板，进行适当的剪裁，折成一个长方形盒子 （纸板的厚度忽略不计）．如图，若在正方形硬纸板的四角各剪一个同样大小的正方形，将剩余部分折成一个无盖的长方形盒子．（1）要使折成的长方形盒子的底面积为484cm2，那么剪掉的正方形的边长为多少？ （2）折成的长方形盒子的侧面积为600cm2，那么剪掉的正方形的边长为多少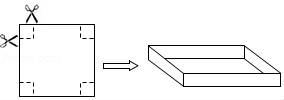？  【解答】解：（1）设减掉的正方形边长为xcm，根据题意得出： （4 0﹣2x）（40﹣2x）=484，解得：x1=9，x2=31（不合题意舍去）， 答：剪掉的正方形边长为9cm； （2）设剪掉的正方形的边长为xcm，此时折成的长方体盒子的侧面积为60 0cm2，依题意，得：4（40﹣2x）x=600 整理，得：x2﹣20x+75=0 解得：x1=5，x2=15 经检验 ，均符合题意．答；剪掉的正方形的边长为5cm或15cm． 22．（12分）先阅读下列的解答过程，然后作答： 形如  的化简，只要我们找到两个数a、b使a+b=m，ab=n，这样（ ）2+（ ）2=m， •= ，那么便有= = ± （a＞b）例如：化简 解：首先把 化为 ，这里m=7，n=12；由于4+3=7，4×3=12，即（  ）2+（ ）2=7， •= ，∴  = = =2+由上述例题的方法化简： （1）  ；（2）  ；（3）  ．【解答】解：（1）  = = ﹣ ；（2）  = = = ﹣ ；（3）  = = ．23．（12分）如图，A、B、C、D为矩形的四个顶点，AB=16cm，AD=6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达B为止，点Q以2cm/s的速度向D移动． （1）P、Q两点从出发开  始到几秒时，四边形PBCQ的面积为33cm2；（2）P、Q两点从出发开始到几秒时，点P和点Q的距离是10cm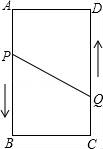．  【解答】解：（1）设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2， 则PB=（16﹣3x）cm，QC=2xcm， 根据梯形的面积公式得  （16﹣3x+2x）×6=33，解之得x=5， （2）设P，Q两点从出发经过t秒时，点P，Q间的距离是10cm， 作QE⊥AB，垂足为E， 则QE=AD=6，PQ=10， ∵PA=3t，CQ=BE=2t， ∴PE=AB﹣AP﹣BE=|16﹣5t|， 由勾股定理，得（16﹣5t）2+62=102， 解得t 1=4.8，t2=1.6．答：（1）P、Q两点从出发开始到5秒时四边形PBCQ的面积为33cm2； （2）从出发到1.6秒或4.8秒时，点P和点Q的距离是10cm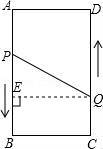．  (责任编辑：admin) |