|
☆☆☆ 点击下载试题 ☆☆☆  2018广安二中中考数学模拟试题【最新Word版】由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ 注意事项： 1、本试卷分为试题卷和答题卡，满分100分，考试时间90分钟； 2、在作答前，考生务必将自己的姓名，班级、考场填写在答题卡规定的地方，并认真核对条形码上的姓名和准考证号。考试结束，只交答题卡。 选择题（每题2分，共20分，每小题均有四个选项，其中只有一项符合题目要求） 3 的相反数是（ ） A．  B． C．3 D．3下列几何体中，正视图是矩形的是（）  A B C D 来自全国各地的知名企业家，聚首某市共签约项目投资总额为90900000元，将90900000 用科学计数法表示正确的是（） A．9.09106 B．0.909108 C．9.09107 D．90.9107 下列运算正确的是( ) A．  B． C．  D． 若m  1，则点P（1－m，m）在（）A．第一象限 B．第二象限 C．第三象限 D．第四象限 如图，螺母的一个面的外沿可以看作是正六边形，这个正六边形ABCDEF的半径是 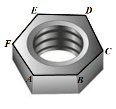 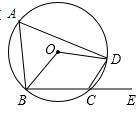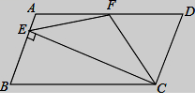cm，则这个正六边形的周长是( )A．  cm B．12 cm C． cm D．36 cm   （第6题图） （第8题图） （第10题图） 7．若不等式  的解集是 ，则 的取值范围是（）a<3 B．a=3 C．a  3 D．a>38．如图，四边形ABCD为圆O 的内接四边形，E是BC 延长线上的一点，已知BOD100， 则DCE的度数为( ) 70° B．60° C．40° D．50° 9．施工队要铺设一段全长2000米的管道，因在高考期间需停工两天，实际每天施工需比原计划多50米，才能按时完成任务，求原计划每天施工多少米．设原计划每天施工x米，则据题意所列方程正确的是（ ）  B． C． D． 10. 如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是______．①∠DCF=  ∠BCD；②EF=CF；③S△BEC=2S△CEF；④∠DFE=3∠AEF．①② B．②③④ C．①②④ D．①②③④ 填空题（每题3分，共18分） 11. 若二次根式  有意义，则x的取值范围是。12．分解因式：2x2-8x+8=。 若关于x的方程  有两个不相等的实数根，则k的取值范围是。 OAB三个顶点坐标分别为O（0，0），A（4，6），B（3，0），以O为位似中心，将OAB缩小为原来的 ，则A的对应点 的坐标为。如图，在4×4的方格中(共有16个方格)，每个小方格都是边长为1的正方形．O，A，B分别是小正方形的顶点，则扇形OAB的弧长等于________。(结果保留根号及π) 如图，将正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图放置，点A1，A2，A3…和C!，C2，C3…分别在直线y=x+2和x轴上，则点B2017的坐标是。 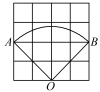 （第15题图） （第16题图） 三、解答题（共62分，要求写出必要的解答步骤和证明过程） (5分)计算：  +( -2008) +  -1 – 6 tan30(5分)先化简  ，再求值，其中x为数据4、5、6、5、3、1、2 的众数。(5分)如图，在直角坐标系中，Rt△ABC位于第一象限，两条直角边BC，BA分别平行于x轴、y轴，点A的坐标为（1，1），AB=2，BC=4． （1）求点C的坐标和AC所在的直线的解析式． （2）若反比例函数y= 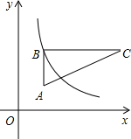 （x＞0）的图象经过点B，求反比例函数解析式； (5分)如图，已知点D在  ABC的BC边上，DE‖AC交AB于E，DF‖AB交AC于F。求证：AE=DF； 若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由。 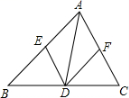 (6分)全面二孩政策定于2016年1月1日正式实施，某中学对七年级部分学生进行了随机问卷调查，其中一个问题“你爸妈如果给你添一个弟弟（或妹妹），你的态度是什么？共有如下四个选项（要求仅选择一个选项）：A非常愿意 B 愿意 C 不愿意 D 无所谓， 如图是根据调查结果绘制的两幅不完整的统计图，请结合图中信息解答以下问题： 试问本次问卷一共调查了名学生；并补全条形统计图； 若该年级共有600名学生，请你估计全年级可能有多少名学生支持（即态度为“非常愿意”和“愿意”）爸妈给自己添一个弟弟（或妹妹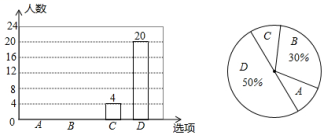）？  在年级活动课上，老师决定从本次调查回答“非常满意”的同学中随机抽取2名同学来谈谈他们的想法.而本次调查回答“非常愿意”的这些同学只有一名女同学，请用树状图或列表的方法选取两名同学中刚好有这名女同学的概率。 (7分)某公司有甲种原料260Kg，乙种原料270Kg，计划用这两种原料生产A、B两种产品共40件。生产每件A种产品需甲种原料8 Kg，乙种原料5 Kg，可获利润900元；生产每件B种产品需甲种原料 4 Kg，乙种原料9 Kg，可获利润1100元。设安排生产A种产品x件。 完成下表
安排生产A、B两种产品的件数有几种方案？试说明理由； 设生产这批40件产品共可获利润y元，将y表示为x的函数，并求出最大利润。 (6分)如图，为了开发利用海洋资源，某勘测飞机预测量一岛屿两端A．B的距离，飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°，然后沿着平行于AB的方向水平飞行了500米，在点D测得端点B的俯角为45°，求岛屿两端AB的距离（结果精确到0.1米， 参考数据：  ） (6分)根据下列材料，解答问题。 等比数列求和： 概念：对于一列数a1,a2,a3,…,an,…(n为正整数)，若从第二个数开始，每一个数与前一个数的比为一定值，即  =q(常数)，那么这一列数a1,a2,a3,…,an,…成等比数列，这一常数q叫作该数列的公比。例：求等比数列  ,  ,  ,…, 的和。解：令S = + + +…+ ①,则3S = 1++ + +…+  ②由②-①得：2S=1- = ，即 S= （1）模仿例题，求等比数列  ,  ,  ,…, 的和；（2）填空：数列  ,  ,…, (a≠1,n为正整数)的公比q=,该数列各项的和为。(写出必要的计算过程)(8分)如图，AB是⊙O的弦，D是半径OA的中点，过D作CD⊥OA交弦AB于点E，交⊙O于F，且CE=CB。 （1）求证：BC是⊙O的切线； （2）连接AF、BF，求∠ABF的度数； 如果CD=15，BE=10，sinA= 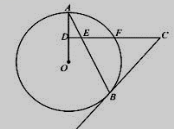 ，求⊙O的半径。 26.(9分)如图，在平面直角坐标系中，顶点为（4，-1）的抛物线交y轴于A点，交x轴与B、C两点（点B在点C的左侧），已知A点的坐标为（0,3）。 （1）求此抛物线的解析式； （2）过点B作线段AB的垂线交抛物线与点D，如果以点C为圆心的圆与直线BD相切于点E，请判断抛物线的对称轴与圆C有怎样的位置关系，并给出证明； （3）已知点P是抛物线上的一个动点，且位于A、C两点之间，问：当点P运动到什么位置时，△PAC的面积最大？并求出此时P点的坐标和△PAC的最大面积。 (责任编辑：admin) |