|
☆☆☆ 点击下载试题 ☆☆☆ 2018乌鲁木齐中考数学冲刺真题【精编Word版可下载】 由于格式问题,部分试题会存在乱码的现象,请考生点击全屏查看! 一.选择题(共10小题,满分36分) 1.下列计算正确的是( ) A. a3﹣a2=a B. a3•a2=a6 C. a3÷a2=a D. (a3)2=a5 2.使二次根式 A. 3.如图所示,把一个正方形对折两次后沿虚线剪下,展开后所得的图形是( ) 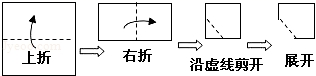 A、 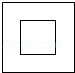 B、 B、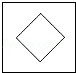 C、 C、 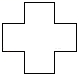 D、 D、  4.下列说法正确的是( ) A.“经过有交通信号的路口,遇到红灯,”是必然事件 B.已知某篮球运动员投篮投中的概率为0.6,则他投10次一定可投中6次 C.处于中间位置的数一定是中位数 D.方差越大数据的波 5. A. 甲 B. 乙 C. 丙 D. 丁 6.阳光公司销售一种进价为21元的电子产品,按标价的九折销售,仍可获得20%,则这种电子产品的 A. 26元 B. 27元 C. 7.为响应承办“绿色奥运”的号召,九年级(1)班全体师生义务 A. C. 8.如图,AC、BD是⊙O直径,且AC⊥BD,  9.一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,使点C落在点C′的位置,BC′交AD于点G(图1);再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M(图2),则EM的长为( ) 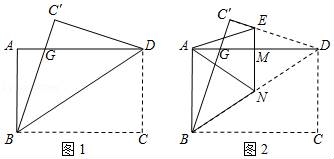 A.2 B. 10.如图,在直角坐 A. 2 B. 3 C. 5 D. 7 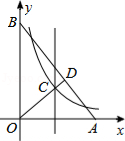 二.填空题(共5小题,满分20分,每小题4分) 11.(4分)计算 12. 如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以对角线OB1为一边作正方形OB1B2C1,再以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3 点B6的坐标 . 13.《“一带一路”贸易合作大数据报告(2017)》以“一 14.(4分)用等分圆周的方法,在半径为1的图中画出如图所示图形,则图中阴影 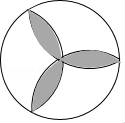 15.(4分)如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点( 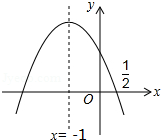 三.解答题 16.(8分)解关于x的不等式组: 17.(8分)先化简,再求值:( 18.(10分)某商场用24000元购入一批空调,然后以每台300 (1)商场第一次购入的空调每台进价是多少元? (2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调 19.(10分)如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADC交BC于F.求证: (1)△ABE≌△CDF; (2)若BD⊥EF,则判断四边形EBFD是什么特殊四边形,请证明你的结论. 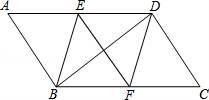 20.(12分)将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方 (1)这部分男生有 (2)这部分男生成绩的中位 (3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率. 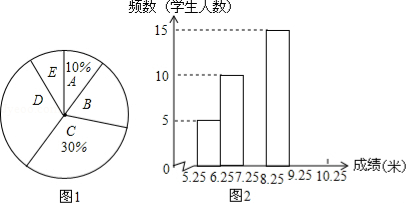 21.(10分)如图,建筑物AB的高为6cm,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)  22.(10分)某学校要制作一批安全工作的宣传材料.甲公司提出:每份材料收费10元 23.(8分)如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P. (1)判断直线PC与⊙O的位置关系,并说明理由; (2)若tan∠P=  24.(6分)一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至乙地.货车的路程y1(km),小轿车的路程y2(km)与时间x(h)的对应关系如图所示. (1)甲乙两地相距多远?小轿车中途停留了多长时间? (2)①写出y1与x的函数关系式; ②当x≥5时,求y2与x的函数解析式; (3)货车出发多长时间与小轿车首次相遇?相遇时与甲地的距离是多少?  25.(8分)如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封 (1)求A、B两点的坐标; (2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC (3)当△BDM为直角三角形时,求m的值.  (责任编辑:admin) |
