|
☆☆☆ 点击下载试题 ☆☆☆  2018年哈尔滨中考数学冲刺试题【精选word版】由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ 一、选择题：（每题3分，共30分） 1．（3分）下列计算正确的是（ ） A．3a﹣2a=a B．  = C．（2a）3=2a3 D．a6÷a3=a22．（3分）对于双曲线y=  ，当x>0时，y随x的增大而减小，则k的取值范围是 ( )A．k<3  B．k≤3 C．k>3 D．k≥33．（3分）下面的图案中，是轴对  称图形而不是中心对称图形的是（ ）A．  B． C． D． 4．（3分）如图，在坡角  为的山坡上栽树，如果相邻两树之间的水平距离为5米，那么这两树的坡面上的距离AB为 ( )A．5cos  米 B． 米 C．5sin米 D． 米 5．（3分）由4个相同的小立方块搭成的几何体如图所示，它的左视图是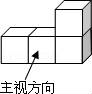（ ）  A．  B． C． D． 6．（3分）不等式组  的解集是（ ）A．  ＜x≤2 B．≤x＜1 C．﹣2＜x≤ D ．﹣2≤x≤7．（3分）一种药品原价每盒25元，经过两次降价后每盒16元，两次降价的百分率相同，设每次降价的百分率为x，则符合题意的方程为（ ） A．16（1+2x）=25 B．25  （1﹣2x）=16 C．16（1+x）2=25 D．25（1﹣x）2=168．（3分）如图，在△ABC中，点D为AB上一点，过点D作BC的平行线交AC于点E，过点E 作 AB的平行线交BC于点F，则下列说法不正确的是 ( ) A. 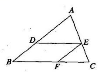 B. C. D.   9 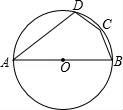 ．（3分）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，点C为 的中点，若∠DAB=50°，则∠ABC的大小是（ ） A．55° B．60° C．65° D．70° 10．（3分）甲、乙两人从少年宫出发，沿相同的路线分别以不同的速度匀速跑向体育馆，甲先跑一段路程后，乙开始出发，当乙超出甲150米时，乙停在此地等候甲，两人相遇后乙又继续以原来的速度跑向体育馆．如图是甲、乙两人在跑步的全过程中经过的路程y（米）与甲出发的时间x（秒）的函数图象，则乙在途中等候  甲用了（ ）秒． A．200 B．150 C．100 D．80 二、填空题（每题3分，共30分） 11．（3分）地球绕太阳公转的速度约为110000千米/时，将这个数用科学记数法表示为 ． 12．（3分）函数y=  中，自变量x的取值范围是 ．13．（3分）把多项式a2b﹣4ab+4b分解因式的结果是 ． 14．（3分）若反比例函数y=  的图象经过点（﹣1，﹣2），则k 的值为 ．15．（3分）不等式组  的 解集是 ．16．（3分）一个扇形的弧长是20  ，面积是240 ，则此扇形的圆心角为 度．17．（3分）已知正方形ABCD中，点E为直线BC上一点，若AE=2BE，则∠DAE= ____________度． 18．（3分）如图，AD和AC分别是⊙O的直径和弦，且∠CAD=30°，OB⊥AD交AC于点B，若OB=5，则BC等于 ．   19．（3分）某商场将一件商品在进价的基础上加价80％标价，再打八折为216元，则这件商品的进价为 元． 20．（3分）如图，在等腰直角三角形ABC中，AB=CB=12，∠ABC=90°，点D为AC上一点，tan∠ADB=3，过D作ED⊥BD，且DE=BD  ，连接BE，AE，EC，点F为EC中点，连接DF，则DF的长为 ． 三、解答题 21．先化简，再求值：  ÷ ﹣ ，其中x=2tan60°﹣4sin30°．22．（6分）如图，正方形ABCD中，点E在AD上，将ACDE绕点C顺时针旋转900至△CFG，点F、点G分别为点D、点E旋转后的对应点，连接EG、DB、DF，DB与CEE交于点M，DF与CG交 于点N (1)求证：BM=DN； (2)直接写出图中已经存在的所有等腰直角三角形．  23．（6分）某报社为了解市民对“社会主义核心价值观”的知晓程度，采取随机抽样的方式进行问题卷调查，调查结果分为“A非常了解”、“B了解”、“C基本了解”三个等级，并根据调查结果制作了如下两幅不完整的统计图．  （1）这次调查  的市民有多少人？（2）补全条形统计图； （2）若该市约有市民950万人，请你根据抽样调查的结果，估计该市有多少万人对“社会主义核心价值观”达到“A非常了解”的程度． 24．如图1，四边形ABCD中，AC⊥BD于点O，点E、F、G、H分别为边AB、BC、CD、AD的中点，连接EF、FG、GH与EH． （1）求证：四边形EFGH为矩形； （2）如图2  ，连接FH，若FH经过点O，在不添加任何辅助线的情况下，请直接写出图中面积相等的矩形． 25．某运输公司承担了某标段的土方运输任务，公司已派出大小两种型号的渣土运输车运输土方，已知2辆大型渣土运输车与3辆小型渣土运输车每次共35吨，3辆大型渣土运输车和2辆小型渣土运输车每次共运40吨． （1）一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨？ （2）该运输公司决定派出大小两种型号的渣土运输 车共20辆参与运输土方，若每次运输土方总量不小于150吨，问该运输公司最多派出几辆小型渣土运输车？26．如图1，⊙O中，AB为直径，弧BC=弧AC，点P在⊙O上，连接PC交AB于点E，过C作PC的垂线交⊙O于点Q （1）求证：弧AP=弧BQ； （2）如图2，点F在弧AC上，∠FEA=∠QEB=30°，连接PF，求证：PF=AO； （3）在（2）的条件下，如图3，过E作EG⊥FP于点G，若EG=6，求OE的长．  27．在平面直角坐标系中，0为坐标原  点，直线y=-x+c与x轴交于点B，与y轴交于点C，抛物线y=a(x+1)(x－3)经过B、C两点，与x轴交于另一点A．(1)如图l，求a的值； (2)如图2，点P在  第一象限的抛物线上，连接黝，交y轴于点D，交直线BC于点E，当PE=AD时，求点P的坐标；(3)如图3，在(2)的条件下，点Q在第二象限的抛物线上，QF⊥x轴于点F，点G在线段OB上，0G=20F，PG交BQ于点H，交BC于点M，若∠QHG一2∠GBH=450，求点Q的坐标．  (责任编辑：admin) |