|
☆☆☆ 点击下载试题 ☆☆☆ 为了方便大家阅读请点击全屏查看  一、选择题(本大题共10小题,每小题3分,共30分) 1、如图所示,点P到直线l的距离是( ). A.线段PA的长度 B.线段PB的长度 C.线段PC的长度 D.线段PD的长度 2、若代数式 A.x=0 B.x=4 C.x ≠0 D.x≠ 4 截至2016年底,国家开发银行对“一代一路”沿线国家累计发放贷款超过1600亿美元,其中1600亿用科学记数法表示为( ). A. 4、有理数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( ). 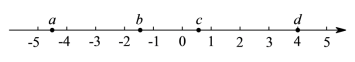 A. 方程 A.x=3 B.x=4 C.x =5 D.x=-5 下列图形中,是轴对称图形但不是中心对称图形的是( ). A 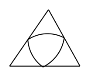 B B 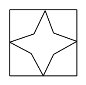 C C D D 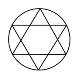 一种药品原价每盒25元,经过两次降价后每盒16元.设两次降价的百分率都为x,则x满足( ). A. 在Rt△ABC中,∠C=90º,AB=4,AC=1,则cosB的值为( ). A. 若直线 A.3 B.4 C.5 D.6 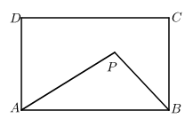 10、如图,在矩形ABCD中,AB=5,AD=3,动点P满足 A. 二、填空题(本大题共6小题,每小题3分,共18分) 11、分解因式: 12、如图,每个正方形的边长为1,A、B、C是小正方形的顶点,则tan∠ABC为 . 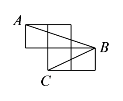 13、两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点0,其摆放方式如图所示,则∠AOB等于 .  14、若关于x的一元二次方程 15、如图,已知扇形OAB的圆心角为60º,扇形的面积为6 16、如图,AB为⊙O的直径,C、D为⊙0上的点, 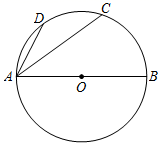  三、解答题(本大题共9小题,共102分) 17、化简: 18、解不等式组  ,并把它的解集在数轴上表示出来. ,并把它的解集在数轴上表示出来. 19、已知,如图,平行四边形ABCD中,E是边BC的中点,连DE并延长交AB的延长线于点F,求证:AB=BF. 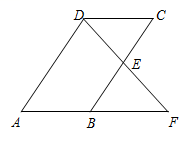 20、中华文明,源远流长.中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
根据所给信息,解答下列问题: (1)m= ,n= . (2)补全频数分布直方图.
(3)这200名学生成绩的中位数会落在 分数段. (4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人? 21、去年某学生返乡创业,投入20万元创办农家乐(餐饮+住宿),一年时间就收回投资的80%,其中餐饮利润是住宿利润的2倍还多1万元. (1)求去年该农家乐餐饮和住宿的利润各为多少万元? (2)今年该学生把去年的餐饮利润全部用于继续投资,增设了土特产的实体店销售和网上销售项目.他在接受记者采访时说:我预计今年餐饮和住宿的利润比去年会有10%的增长,加上土特产销售的利润,到年底除收回所有投资外,还将获得不少于10万元的纯利润.”请问今年土特产销售至少有多少万元的润? 22、如图,AB为⊙O的直径,C为⊙O一点,AD和过点C的切线互相垂直,垂足为D. 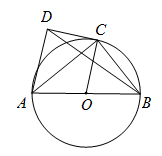 (1)求证:AC平分∠DAB. (2)若sin∠ABC= 23、如图,在平面直角坐标系中,函数 (1)求k、m的值. (2)已知点P(n,n)(n>0),过点P作平行于x轴的直线,交直线 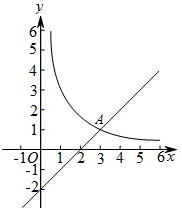 ①当n=1时,判断线段PM与PN的数量关系,并说明理由. ②若PN≥PM,结合函数的图象,直接写出n的取值范围. 24、如图,已知二次函数 (1)求此二次函数的关系式. (2)判断∆ABC的形状.若∆ABC的外接圆记为⊙M,请直接写出圆心M的坐标. 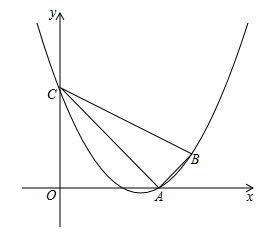 (3)若将抛物线沿射线BA方向平移,平移后点A、B、C的对应点分别记为点 25、如图,已知抛物线的对称轴是y轴,且点(2,2),(1, (1)求抛物线的解析式及顶点N的坐标. (2)求证:四边形PMDA是平行四边形. (3)求证:∆DPE∽∆PAM,并求出当它们的相似比为 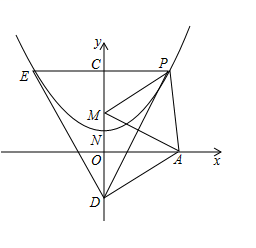  (责任编辑:admin) |

