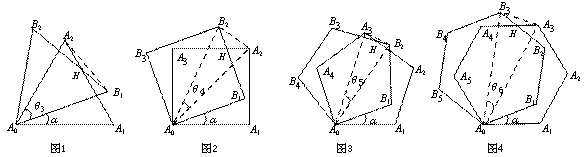
|
中考规律探究题的构建与应用 江西省安福县城关中学 曹经富 规律猜想题作为一种重要的研究问题的方法和探索发现新知识的重要手段，非常有利于同学们创造性思维能力的培养与训练，它不仅给中考试题的形式和内容注入了新的活力，而且给当前的课堂学习带来了重大影响，这种试题一般是在特定的背景、情境或某些条件下（可以是函数关系式、有规律的数或式、特定的生活情景、流程图、某种特征的图形、图案或图表），认真分析，仔细观察，提取相关的数据、信息，进行适当的分析、综合归纳，作出大胆猜想，得出结论，进而加以验证或解决问题的数学探索题。其解题思维过程是：从特殊情况入手→探索发现规律→综合归纳→猜想得出结论→验证结论， 为此要求我们能在一定的背景或特定的条件（已知条件或所提供的若干个特例）下，通过观察、分析、比较、概括、归纳和猜想，从中发现有关数学对象所具有的某种规律或不变性的结论和数学本质的内容，进而利用这个规律或结论进一步解决相关的实际问题。它体现了“从特殊到一般”及转化的数学思想方法，一般的解题思路是通过观察，进而寻找规律，猜想出相关的结论并加以验证。出现的形式可能以填空、选择或解答为主．现结合2010年中考试题来说明规律猜想题的构建与应用，希望能给大家带来一定的启示与帮助． 一、在图形的叠加中构建与应用 例1（2010湖南衡阳）如下图是一组有规律的图案，第1个 图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第n(n是正整数)个图案中由 个基础图形组成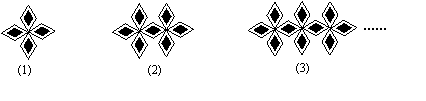．  -思路点拨与解析：从前三个图形可找出规律，第1个图案基本图形的个数为：4=1×3+1；第2个图案基本图形的个数为：7=2×3+1；第3个图案基本图形的个数为：10=3×3+1；… …，所以第n个图案基本图形的个数为：n×3+1=3n+1. 点评：解这类问题的关键在于从简单的情形入手，逐个观察、发现、归纳图形中的变化规律、变化趋势及不变化的量，寻找出内在的规律与图案叠加个数之间关系式构建相应的数学模型，主要是考查我们的观察能力、发现能力、分析判断能力、逻辑推理能力和猜想规律能力． 二、在数列或等式中构建与应用 例2（2010广东中山）阅读下列材料：  ， ， ，由以上三个等式相加，可得  读完以上材料，请你计算下列各题： （1）  （写出过程）；（2）  = ；（3）  = ．思路点拨与解析：在所给的一系列等式中，既要观察横向的变化规律，也要观察纵向的变化规律：等式左边的第一列数比第二列数小１，等式右边的第一列数  为常量，括号内的列数也依次递增１。（1） =  + +…+ =  =440．（2）  （3） =  + +…+  = =1260点评：解这类问题的关键在于既要从整体上把握数列的横向的变化规律或趋势及不变量，又要从整体上把握数列的纵向的变化规律或趋势及不变量，根据数列的特征选用恰当的代数式或等式进行准确表示． 三、在流程图中构建与应用 例3 如图所示的运算程序中，若开始输入的  值为48，我们发现第1次输出的结果为24，第2次输出的结果为12，……第2011次输出的结果为___________． 思路点拨与解析：这是一道分类考虑的程序流程题，解题的关键是确定输入的数据是奇数还是偶数，再按要求选择相应的代数式将傎代入求解，通过计算，会发现从第3次开始，这个程序输出的将以6、3、6、3循环，每两次一循环，由此20011-2=2009=1004×2+1，从而判断出第2011次输出的结果为6. 点评：这是一道以数字转换循环计算为背景的代入求傎的程序题，解题的关键是弄清流程图所表示的含义，要注意确定代入的数根据奇、偶性选择相应的代数式徨计算． 四、在表格中构建与应用 例4（2010年贵州遵义）小明玩一种的游戏,每次挪动珠子的颗数与对应所得的分数如下表:
当对应所得分数为132分时,则挪动的珠子数为 颗. 思路点拨与解析：观察表格可发现规律，挪动珠子数n+1颗，则对应所得分数为n(n+1)分。由此可建立方程得n(n+1)=132，解得n=11，故挪动的珠子数为12颗 点评：这类以表格为载体，需要从中获取解题信息。解这类问题的关键在于结合表格中所给数据，分析、发现出表格中横行与纵列各个数据之间的内在联系，从特殊到一般，并用与表格相关的序列、数字、相应的字母、代数式等表示出表格中数列横向与纵向的变化趋势或规律． 五、在函数图象中构建与应用 例5(2010福州)如图，直线  ，点A1坐标为（1，0），过点A1作x轴的垂线交直线于点B1，以原点O为圆心，OB1长为半径画弧交x轴于点A2；再过点A2作x轴的垂线交直线于点B2，以原点O为圆心，OB2长为半径画弧交x轴于点A3，…，按此做法进行下去，点A5的坐标为 ． 思路点拨与解析：由直线 ，可知 ，得到 ，得到 ，可知 的坐标为（２,０）,同理可知 的坐标为（４,０）…， 的坐标为（ ，０）点评：先探讨某种情境中简单情况下存在的某个结论，然后进一步推广到一般情况下，这是探究问题的一种经验或一种模式，这种思维方式或者说解题方法应引起我们的关注与重视．解题的关键是如何选择切入点及由特殊到一般或由简单到复杂的思维模式，利用类比的数学思想解决问题，这些本质相同的问题解决办法是都进行列举与归纳推理，即从列举对象的一切特殊情形的前提中，推出关于全部对象的一般结论的推理方法． 六、在生活图景中构建与应用 例6（2010年湖北省恩施州）(1)计算:如图①,直径为  的三等圆⊙O 、⊙O 、⊙O 两两外切，切点分别为A、B、C ，求OA的长（用含的代数式表示）.   （２）探索:若干个直径为 的圆圈分别按如图②所示的方案一和如图③所示的方案二的方式排放，探索并求出这两种方案中 层圆圈的高度 和 （用含 、的代数式表示）.（3）应用:现有长方体集装箱，其内空长为5米，宽为3.1米，高为3.1米.用这样的集装箱装运长为5米，底面直径（横截面的外圆直径）为0.1米的圆柱形钢管，你认为采用（2）中的哪种方案在该集装箱中装运钢管数最多？并求出一个这样的集装箱最多能装运多少根钢管？（  ≈1.73）思路点拨：有关两圆相切的问题，常作圆心距，在图①，通过添加辅助线构造等边三角形，O A恰好为等边三角形的高，借助勾股定理便可求解；在图③中，一层的高度恰好为，两层的高度恰好为 + ，三层的高度恰好为+  ，四层的高度恰好为 +  ，层圆圈的高度＝+  。解析：(1)∵⊙O 、⊙O、⊙O两两外切， ∴OO=OO=OO=a， 又∵OA= OA∴O A⊥OO ， ∴OA=  =  ，（2） = ，  = ， (3) 方案二装运钢管最多。即：按图10③的方式排放钢管，放置根数最多. 根据题意，第一层排放31根，第二层排放30根， 设钢管的放置层数为n,可得  解得  ， ∵ 为正整数 ，∴=35钢管放置的最多根数为：31×18+30×17=1068（根） 点评：解这类问题的关键弄清题意，结合图形，将实际问题转化为数学问题，从整体上把握圆形堆放的高度与层数 之间的变化规律或趋势及不变量，根据层数的特征选用恰当的代数式或等式进行准确表示。运用空间思维和想象，进行大胆的猜想，构建相应的数学模型，并用以解决问题．七、在变换操作中构建与应用 例7（2010江西）课题：两个重叠的正多边型，其中一个绕某一顶点旋转所形成的有关问题． 实验与论证 设旋转角∠A1A0B1=α（α< A1A0A2）， θ3，θ4，θ5，θ6，所表示的角如图所示． （1） 用含α的式子表示角的度数：θ3=___________θ4=_____________θ5=____________ |
）．
的度数，应从旋转中有关角度的变与不变上突破；（２）结合图形比较容易得到被
垂直平分的线段，在证明时要充分利用背景中正多边形及旋转中的角度；（３）要探究
的度数，要注意区分正偶数边形及正奇数边形两种情形去思考与求解度数的表达式；（４）要探究正ｎ边形中被
．
．
与
是全等的等边三角形，∴
，∴
，∴
，∴点
在线段
，当
．
．
．