|
☆☆☆ 点击下载试题 ☆☆☆ 请点击全屏查看 2017沈阳市铁西一模数学试题 选择题 1.计算:(−5)+3的结果是( ) A. −8 B. −2 C. 2 D. 8 2.把多项式m2−9m分解因式，结果正确的是( ) A.m(m−9) B.(m+3)(m−3) C.m(m+3)(m−3) D.(m−3)2 3.在下面几何体中,其俯视图是三角形的是( ) A.  B.  C.  D.  4（2017沈阳数学）.2016年国庆节期间,沈阳共接待游客约657.9万人次,657.9万用科学记数法表示为( ) A. 0.6579×103 B. 6.579×102 C. 6.579×106 D. 65.79×105 5.某校调查了20名男生某一周参加篮球运动的次数,调查结果如表所示,那么这20名男生该周参加篮球运动次数的平均数是( )
A. 3次 B. 3.5次 C. 4次 D. 4.5次 6.在平面直角坐标系中，点A在第一象限，点B在x轴正半轴上，∠AOB=60°，OA=8.点A的坐标是（ ） A. （4,8） B. （4,4  ） C. （4 ,4） D.（8,4）如图，正五边形ABCDE的对角线BD、CE相交于点F，则下列结论正确的是（ ） A. ∠BCE=36° B.△BCF是直角三角形 C. △BCD≌△CDE D.AB⊥BD  8.分式方程  的解是（ ）A. x=−2 B. x=-3 C. x=2 D. x=3 9.（2017沈阳数学）已知点A(-2,y1)、B(-4,y2)都在反比例函数y=kx(k<0)的图象上,则y1、y2的大小关系为 A. y1>y2 B. y1  A. ①② B. ①③ C. ②③ D. ②填空题 11.计算：2a3÷a___________ 12.学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数  (单位：分)及方差s2如表所示：
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是_____ 若关于x的一元二次方程x2−4x+p=0有两个不相等的实数根，则p的取值范围是 14.（2017沈阳数学）如图，AB∥CD，点E是线段CD上的一点，BE交AD于点F，EF=BF,CD=10，AB=8，CE=_____ 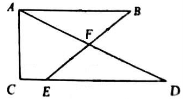 15.不等式组  的所有整数解的和是________16.如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(-2,-3).直线  与OC、AB分别交于点D、E，点P在矩形的边AB或BC上，作PF⊥ED于点F，连接PD，当△PFD是等腰三角形时，点P的坐标为 . 三、（6分、8分、8分） 17.（2017沈阳数学）已知x,y满足方程组  ，求代数式(x−y)2−(x+2y)(x−2y)的值。如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=  BD，连接DN、MN.若AB=6。（1）求证：MN=CD； （2）求DN的长  甲、乙两个不透明的口袋，甲口袋中装有2个分别标有数字1，2的小球，乙口袋中装有3个分别标有数字3，4，5的小球，它们的形状、大小完全相同， （1）随机从乙口袋中摸出一个小球，上面数字是奇数的概率为________ （2）现随机从甲口袋中摸出一个小球记下数字，再从乙口袋中摸出一个小球记下数字。 请用列表或树状图的方法，求出两个数字之和能被5整除的概率。 四、（2017沈阳数学）（8分、8分） 20.某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行加价收费. 为更好地决策，自来水公司随机抽取了部分用户的用水量数据，并绘制了如下不完整的统计图（每组数据包括右端点但不包括左端点）. 用户用水量频数分布直方图 用户用水量扇形统计图  请你根据统计图解答下列问题： （1）此次抽样调查的总户数是 户；扇形图中“10吨-15吨”部分的圆心角的度数是 度； （2）求“15吨-20吨”部分的户数，并补全频数分布直方图； （3）如果自来水公司将基本用水量定为每户25吨，那么该地区120万用户中约有多少用户的用水全部享受基本价格？ 某水果批发商计划用8辆汽车装运甲、乙两种水果共22吨（每种水果不少于一车）到外地销售，每辆汽车载满是能装甲种水果2吨或乙种水果3吨，每辆汽车规定满载，并且只能装一种水果，求装运甲、乙两种水果的汽车各多少辆？ 五、（2017沈阳数学）（10分、10分、12分、12分） 22.如图，以□ABCD的边AB为直径作⊙O，边CD与⊙O相切于点E，边AD与⊙O相交于点F，已知AB=12，∠C=60° （1）求弧EF的长； （2）线段CE的长为 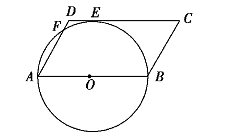 23.如图，在平面直角坐标系中，直线y=x+3与x轴交于点B，与直线CD交于点A（  ，a），点D的坐标为（0， ），点C在x轴上（1）求a的值 （2）求直线CD的解析式； （3）若点E是直线CD上一动点（不与点C重合），当△CBE∽△COD时，求点E的坐标. 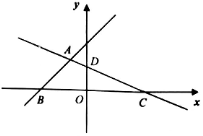 24.（2017沈阳数学）在△ABC中,∠ACB﹤90∘,以AB为一边作等边△ABD，且点D与点C在直线AB同侧，平面内有一点E与点D分别在直线AB两侧，且BE=BC，∠ABE=∠DBC，连接CD、AE，AC=5，BC=3 求证：CD=AE； 点E关于直线AB的对称点为点F，判断△BFC的形状，并说明理由； 在（2）的条件下，当线段CD最短时，请直接写出四边形AEBF的面积。 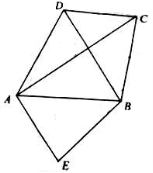 25（2017沈阳数学）在平面直角坐标系中，抛物线  经过点A（-1,0）和点B（2，-1），交y轴于点C，BD⊥x轴于点D，连接AB、AC.求抛物线的函数表达式； 点P是抛物线上在直线AB下方的动点，直线PH⊥x轴，交AB于点H，当PH=  时，求点P的坐标；将△AOC沿y轴向上平移，将△ABD沿x轴向左平移，两个三角形同时开始平移，且平移的速度相同。设△AOC平移的距离为t，平移过程中两个三角形重叠部分的面积为S，当0＜t＜  时，请直接写出S与t的函数表达式及自变量t的取值范围。    (责任编辑：admin) |
