|
☆☆☆ 点击下载试题 ☆☆☆  2018学年齐齐哈尔中考数学冲刺试卷【精选word版 含答案】由于格式问题，部分试题会存在乱码的现象，请考生点击全屏查看！ 一、选择题（共10小题，每小题3分，满分30分） 1．（3分）下列各组图形中，不相似的是（ ） A．有一个角是35°的两个等腰三角形 B．两个等边三角形 C．两个等腰直角三角形 D．有一个角是120°的两个等腰三角形 2．（3分）在△ABC中，∠C=90°，D是边AB上一点（不与点A，B重合），过点D作直线与另一边相交，使所得的三角形与原三角形相似，这样的直线有（ ） A．1条 B．2条 C．3条 D．4条 3．（3分）如图，AB是半圆O的直径，弦AD、BC交于E，∠BED=α，则  等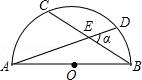于（ ）4．  A．sinα B．cosα C．tanα D．  4．（3分）如图，在平 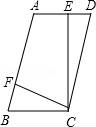 行四边形ABCD中，AB=10，AD=6，E是AD的中点，在AB上取一点F，使△CBF∽△CDE，则BF的长是（ ） A．5 B．8.2 C．6.4 D．1.8 5．（3分）如图，CD是平面镜，光线从A点出发经CD上点E反射后照射到B点，若入射角为α，AC⊥CD，BD⊥CD，且AC=3，BD=6，CD=11，则tanα值为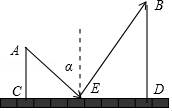（ ）  A．  B． C． D． 6．（3分）设a、b、c分别为△ABC中∠A、∠B和∠C的对边，则△ABC的面积为（ ） A．  B． C． D． 7．（3分）如图，点A是反比例函数y= 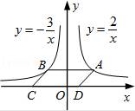 （x＞0）的图象上任意一点，AB∥x轴交反比例函数y=﹣ 的图象于点B，以AB为边作▱ABCD，其中C、D在x轴上，则S□ABCD为（ ） A．2 B．3 C．4 D．5 8．（3 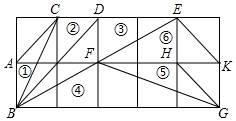 分）如图，在正方形网格上有6个三角形①△ABC，②△BCD，③△BDE，④△B FG，⑤△FGH，⑥△EFK，其中②～⑥中与三角形①相似的是（ ） A．②③④ B．③④⑤ C．④⑤⑥ D．②③⑥ 9．（3分）如图，由几个相同的小正方体搭成的几何体的主视图和俯视图，组成这个几何体的小正方体的个数是（ ）  A．5个或6个 B．6个或7个 C．7个或8个 D．8个或9个 10．（3分）如图，二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为直线x= 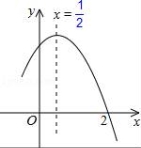 ，且经过点（2，0），下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（﹣2，y1），（ ，y2）是抛物线上的两点，则y1＜y2，其中说法正确的是（ ） A．①②④ B．③④ C．①③④ D．①② 二.填空（每空3分，满分30分） 11．（3分）一个四边形的四边长分别是3、4、5、6，另一个和它相似的四边形的最小边长为6，那么后一个四边形的周长为 ． 12．（3分）已知：关于抛物线y=2x2+3x+m﹣1与x轴有两个交点，则m的取值范围为 ． 13．（3分）如图，为测量学校旗杆的高度，小东用长为3.2m的竹竿做测量工具．移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为 m．  14．（3分）如图已知△ABC的一边BC与以AC为直径的⊙O相切于点C，若BC=4，AB=5，则sinB= 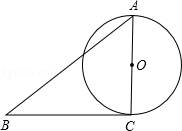．  15．（3分）如图，DE是△ABC的中位线，M是DE的中点，CM的延长线交AB于N，若S△DMN=1，则 S四边形ANME= 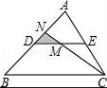．  16．（3分）已知△ABC和△A′B′C′是关于点O位似，若AO=3cm，位似比为4：9，则A′O=  ．17．（3分）若反比例函数y=  和一次函数y=3x+b的图象有两个交点，且有一个交点的纵坐标为6，则b= ．18．（3分）反比例函数y=（2k+1）  在每个象限内y随x的增大而增大，则k= ．19．（3分）抛物线y=ax2+bx+c上部分点的坐标对应值如下表：
从上表可知，下列说法中正确的是 ．（填写序号） ①函数y=ax2+bx+c的最大值为6；②抛物线与x轴的一个交点为（3，0）；③在对称轴右侧，y随x增大而减小； ④抛物线的对称轴是直线x=  ；⑤抛物线开口向上．20．（3分）如图所示，已知直线 与x、y轴交于B、C两点，A（0，0），在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…则第n个等边三角形的边长等于 ．  三.解答题（本题包括8个小题，满分60分） 21．（11分）（1）计算：  ﹣2cos245°+2 （2）先化简，再求值：（   ） ，其中a=tan60°﹣1．22．（6分）如图，在△ABC中，∠B=45°，∠C=60°，AB=6，求△ABC的面积．  23．（6分）如图，已知△ABC的三个顶点的坐标分别为A（﹣1，2）、B（﹣3，0）、C（0，0）、 （1）请直接写出点A关于x轴对称的点A′的坐标； （2）以C为位似中心，在x轴下方作△ABC的位似图形△A1B1C1，使放大前后位似比为1：2，请画出图形，并求出△A1B1C1的面积； （3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点  D的坐标． 24．（7分）如图，已知A（﹣4，n），B（2，﹣4）是一次函数y=kx+b的图象和反比例函数y=  的图象的两个交点．（1）求反比例函数和一次函数的解析式；[来源:ZXXK] （2）求直线AB与x轴的交点C的坐标及△AOB的面积； （3）求方程kx+b﹣  =0的解（请直接写出答案）；（4）求不等式kx+b﹣ ＜0的解集（请直接写出答案）． 25．（7分）如图，海岛A四周20海里周围内为暗礁区，一艘货轮由东向西航行，在B处见岛A在北偏西60°，航行24海里到C，见岛A在北偏西30°，货轮继续向西航行，有无触礁的危险？请说明理由．（  ） 26．（7分）阅读理解题：下面利用45°角的正切，求tan22.5°的值，方法如下： 解：构造Rt△ABC，其中∠C=90°，∠B=45°，如图． 延长CB到D，使BD=AB，连接AD，则∠D= ∠ABC=22.5°．设AC=a，则BC=a，AB=BD=  a．又∵CD=BD+CB=（1+ ）atan22.5°=tan∠D= ﹣1请你仿照此法求tan15°的值．  27．（8分）如图，抛物线y=  x2+bx﹣2与x轴交于A，B两点，与y轴交于C点，且A（﹣1，0）．（1）求抛物线的解析式及顶点D的坐标； （2）判断△ABC的形状，证明你的结论； （3）点M（m，0）是 x轴上的一个动点，当MC+MD的值最小时，求m的值． 28．（8分）如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根． （1）求C点坐标； （2）求直线MN的解析式； （3）在直线MN上存在点P，使以点P，B，C三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．   2018学年齐齐哈尔中考数学冲刺试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分） 1．（3分）下列各组图形中，不相似的是（ ） A．有一个角是35° 的两个等腰三角形B．两个等边三角形 C．两个等腰直角三角形 D．有一个角是120°的两个等腰三角形 【解答】解：所有等边三角形都相似，所有等腰直角三角形都相似，故B、C可以判断相似； 有一个角是35°，如果一个三角形的顶角为35°，另一三角形的底角为35°则这两个等腰三角形不相似，故A不能判断相似；[来源:学#科#网] 有一个角是120°，由于这个角为钝角，只能是两个等腰三角形的顶角，可判断两个等腰三角形相似； 故选：A． 2．（3分）在△ABC中，∠C=90°，D是边AB上一点（不与点A，B重合），过点D作直线与另一边相交，使所得的三角形与原三角形相似，这样的直线有（ ） A．1条 B．2条 C．3条 D．4条 【解答】解：过点D作AB的垂线，或作AC的垂线，作BC的垂线共三条直线，故选C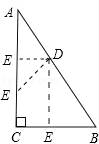．  3．（3分）如图，AB是半圆O的直径，弦AD、BC交于E，∠BED=α，则 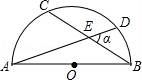等于（ ） A．sinα B．cosα C．tanα D．  【解答】解：连接BD． ∵AB是⊙O的直径， ∴∠BDE=90°． 根据同弧所对的圆周角相等得： ∠A=∠C，∠CDE=∠ABE， ∴△ECD∽△EBA． ∴ = ，∵cosα= ，∴ =cos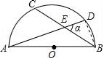α，故选：B．  4．（3分）如图，在平行四边形ABCD中，AB=10，AD=6，E是AD的中点，在AB上取一点F，使△CBF∽△CDE，则BF的长是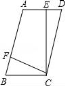（ ）  A．5 B．8.2 C．6.4 D．1.8 【解答】解：∵在平行四边形ABCD中，AB=10，AD=6，E是AD的中点， ∴CD=10，BC=6，DE=3． ∵△CBF∽△CDE， ∴BF：DE=BC：DC， ∴BF=6÷10×3=1.8． 故选：D． 5．（3分）如图，CD是平面镜，光线从A点出发经CD上点E反射后照射到B点，若入射角为α，AC⊥CD，BD⊥CD，且AC=3，BD=6，CD=11，则tanα值为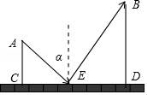（ ）  A． B． C． D． 【解答】解：∵AC⊥CD，BD⊥CD， ∴∠ACE=∠BDE=90°， 又∵∠AEC=∠BED， ∴△ACE∽△BDE， ∴  = = ，∴DE=2CE， 又∵CD=11， ∴CE=  ，∴tanα=tanA=  = ．故选：B． 6．（3分）设a、b、c分别为△ABC中∠A、∠B和∠C的对边，则△ABC的面积为（ ） A．  B． C． D． 【解答】解：过点A作b边上的高AD， 则Rt△ACD中， AD=AC•sinC=bsinC， △ABC的面积等于 abs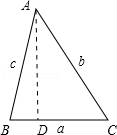inC．故选：C．  6．（3分）如图，点A是反比例函数y= 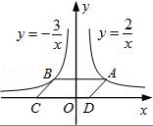 （x＞0）的图象上任意一点，AB∥x轴交反比例函数y=﹣ 的图象于点B，以AB为边作▱ABCD，其中C、D在x轴上，则S□ABCD为（ ） A．2 B．3 C．4 D．5 【解答】解：设A的纵坐标是b，则B的纵坐标也是b． 把y=b代入y= 得，b=，则x= ，即A的横坐标是，；同理可得：B的横坐标是：﹣  ．则AB=  ﹣（﹣ ）= ．则S□ABCD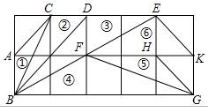= ×b=5．故选：D． 9．（3 分）如图，在正方形网格上有6个三角形①△ABC，②△BCD，③△BDE，④△BFG，⑤△FGH，⑥△EFK，其中②～⑥中与三角形①相似的是（ ） A．②③④ B．③④⑤ C．④⑤⑥ D．②③⑥ 【解答】解：设第个小正方形的边长为1，则△ABC的各边长分别为1、  、 ．则②△BCD的各边长分别为1、 、2；③△BDE的各边长分别为2、2 、2（为△ABC对应各边长的2倍）；④△BFG的各边长分别为5、  、 （为△ABC对应各边长的倍）；⑤△FGH的各边长分别为2、 、（为△ABC对应各边长的倍）；⑥△EFK的各边长分别为3、  、 ．根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤． 故选：B． 10．（3分）如图，由几个相同的小正方体搭成的几何体的主视图和俯视图，组成这个几何体的小正方体的个数是（ ）  A．5个或6个 B．6个或7个 C．7个或8个 D．8个或9个 【解答】解：从俯视图可得最底层有4个个小正方体，由主视图可得上面一层是2个或3小正方体， 则组成这个几何体的小正方体的个数是6个或7个； 故选：B． 11．（3分）如图，二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为直线x= 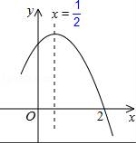 ，且经过点（2，0），下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（﹣2，y1），（ ，y2）是抛物线上的两点，则y1＜y2，其中说法正确的是（ ） A．①②④ B．③④ C．①③④ D．①② 【解答】解：①∵二次函数的图象开口向下， ∴a＜0， ∵二次函数的图象交y轴的正半轴于一点， ∴c＞0， ∵对称轴是直线x= ，∴﹣  =，∴b=﹣a＞0， ∴abc＜0． 故①正确； ②∵由①中知b=﹣a， ∴a+b=0， 故②正确； ③把x=2代入y=ax2+bx+c得：y=4a+2b+c， ∵抛物线经过点（2，0）， ∴当x=2时，y=0，即4a+2b+c=0． 故③错误； ④∵（﹣2，y1）关于直线x= 的对称点的坐标是（3，y1），又∵当x＞  时，y随x的增大而减小， ＜3，∴y1＜y2． 故④正确； 综上所述，正确的结论是①②④． 故选：A． 二.填空（每空3分，满分30分） 11．（3分）一个四边形的四边长分别是3、4、5、6，另一个和它相似的四边形的最小边长为6，那么后一个四边形的周长为 36 ． 【解答】解：3+4+5+6=18， 设后一个四边形的周长为x， ∵两个四边形相似， ∴  = ，解得x=36． 故答案为：36． 12．（3分）已知：关于抛物线y=2x2+3x+m﹣1与x轴有两个交点，则m的取值范围为 m＜  ．【解答】解：∵关于抛物线y=2x2+3x+m﹣1与x轴有两个交点， ∴方程2x2+3x+m﹣1=0的△＞0， 即△=32﹣4×2×（m﹣1）＞0， 解得：m＜ ，故答案为：m＜ ．12．（3分）如图，为测量学校旗杆的高度，小东用长为3.2m的竹竿做测量工具．移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为 12 m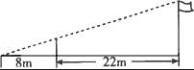．  【解答】解：因为BE∥CD，所以△AEB∽△ADC， 于是  = ，即 = ，解得：CD=12m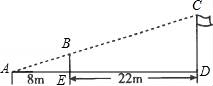．旗杆的高为12m．  13．（3分）如图已知△ABC的一边BC与以AC为直径的⊙O相切于点C，若BC=4，AB=5，则sinB= 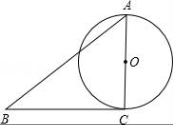 ． 【解答】解：∵BC是⊙O的切线， ∴∠ ACB=90°，∴在直角△ABC中，AC=  = =3，∴sinB=  = ．故答案是： ．15．（3分）如图，DE是△ABC的中位线，M是DE的中点，CM的延长线交AB于N，若S△DMN=1，则 S四边形ANME= 5 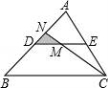．  【解答】解：DE是中位线，M是DE中点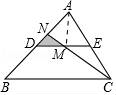，  ∴DM：BC=1：4， ∴DN：DB=1：3，AN：DN=1：2， ∴S△NDM：S△ANM=1：2． ∴S△ADM=S△AME， ∴S△NDM：S四边形ANME=1：5． ∵S△DMN=1， ∴S四边形ANME=5， 故答案为：5 16．（3分）已知△ABC和△A′B′C′是关于点O位似，若AO=3cm，位似比为4：9，则A′O= 6.75cm ． 【解答】解：∵△ABC和△A′B′C′的位似比为4：9， ∴其对应边的比为4：9， ∵AO=3cm， ∴A′O=6.75cm． 故答案为：6.75cm． 17．（3分）若反比例函数y=  和一次函数y=3x+b的图象有两个交点，且有一个交点的纵坐标为6，则b= 5 ．【解答】解：把y=6得： =6，则x= ，代入y=3x+b，得3x+b=6，则x=  ，根据题意得： =，解得：b=5．故答案是：5． 18．（3分）反比例函数y=（2k+1）  在每个象限内y随x的增大而增大，则k= ﹣1 ．【解答】解：由于反比例函数y=（2k+1） 在每个象限内y随x的增大而增大，则k需满足：k2﹣2=﹣1且2k+1＜0， 则k=﹣1． 故答案为：﹣1． 19．（3分）抛物线y=ax2+bx+c上部分点的坐标对应值如下表：
从上表可知，下列说法中正确的是 ②③④ ．（填写序号） ①函数y=ax2+bx+c的最大值为6；②抛物线与x轴的一个交点为（3，0）；③在对称轴右侧，y随x增大而减小； ④抛物线的对称轴是直线x= ；⑤抛物线开口向上．【解答】解：对称轴为：x=  =∴当x= 时取得最大值，∴①错误； 函数图象经过点（﹣2，0）， ∴也经过点（3，0） ∴②正确 观察表格发现在x= 的右侧，y随x增大而减小；故④正确； ∵有最大值， ∴开口向下， ⑤错误， 故答案为：②③④ 20．（3分）如图所示，已知直线  与x、y轴交于B、C两点，A（0，0），在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…则第n个等边三角形的边长等于 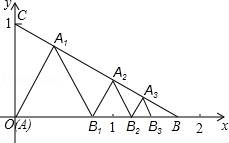 ． 【解答】解：∵直线 与x、y轴交于B、C两点，∴OB=  ，OC=1，∴BC=2， ∴∠OBC=30°，∠OCB=60°． 而△AA1B1为等边三角形，∠A1AB1=60°， ∴∠COA1=30°， ∴∠CA1O=90°． 在Rt△CAA1中，AA1=  OC=，同理得：B1A2= A1B1= ，依此类推，第n个等边三角形的边长等于  ．故答案为： ．三.解答题（本题包括8个小题，满分60分） 21．（11分）（1）计算：  ﹣2cos245°+2 （2）先化简，再求值：（   ） ，其中a=tan60°﹣1．【解答】解：（1）原式=  ﹣2×（ ）2+2×（1﹣）= +1﹣1+2﹣=2； （2）原式=  ﹣ =﹣  • =﹣  ，a=tan60°﹣1=  ﹣1，当a= ﹣1时，原式=﹣  =1﹣ ．22．（6分）如图，在△ABC中，∠B=45°，∠C=60°，AB=6，求△ABC的面积．  【解答】解：过点A作AD⊥BC， ∴∠ADB=90°， ∵∠B=45°，AB=6， ∴在Rt△ADB中，BD=AD=6×  =3，∵∠C=60°， ∴∠CAD=30°， ∴在Rt△ADB中，CD=  AD= ，∴BC=BD+CD=3 + ；∴S=S△ABC= •BC•AD=（3+）×3=9+3 ．答：△ABC的面积是9+3 ． 23．（6分）如图，已知△ABC的三个顶点的坐标分别为A（﹣1，2）、B（﹣3，0）、C（0，0）、 （1）请直接写出点A关于x轴对称的点A′的坐标； （2）以C为位似中心，在x轴下方作△ABC的位似图形△A1B1C1，使放大前后位似比为1：2，请画出图形，并求出△A1B1C1的面积； （3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标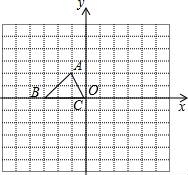．  【解答】解：（1）∵点A的坐标为（﹣1，2）， ∴点A关于x轴对称的点A′的横坐标为﹣1，纵坐标为﹣2， ∴点A′的坐标为（﹣1，﹣2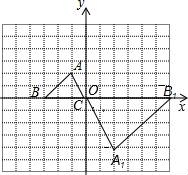）；  （2）△A1B1C1的面积= ×6×4=12；（3）点D的坐标为（﹣2，﹣2），（﹣4，2），（2，2）． 24．（7分）如图，已知A（﹣4，n），B（2，﹣4）是一次函数y=kx+b的图象和反比例函数y=  的图象的两个交点．（1）求反比例函数和一次函数的解析式； （2）求直线AB与x轴的交点C的坐标及△AOB的面积； （3）求方程kx+b﹣ =0的解（请直接写出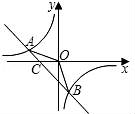答案）；（4）求不等式kx+b﹣ ＜0的解集（请直接写出答案）． 【解答】解：（1）∵B（2，﹣4）在函数y=  的图象上，∴m=﹣8． ∴反比例函数的解析式为：y=﹣  ．∵点A（﹣4，n）在函数y=﹣ 的图象上，∴n=2， ∴A（﹣4，2）， ∵y=kx+b经过A（﹣4，2），B（2，﹣4）， ∴  ，解之得： ．∴一次函数的解析式为：y=﹣x﹣2． （2）∵C是直线AB与x轴的交点，∴当y=0时，x=﹣2． ∴点C（﹣2，0）， ∴OC=2． ∴S△AOB=S△ACO+S△BCO=  OC•n+OC×4=×2×2+×2×4=6．（3）方程kx+b﹣  =0的解，相当于一次函数y=kx+b的图象和反比例函数y=的图象的交点的横坐标，即x1=﹣4，x2=2． [来源:Zxxk.Com] （4）不等式kx+b﹣ ＜0的解集相当于一次函数y=kx+b的函数值小于反比例函数y=的函数值，从图象可以看出：﹣4＜x＜0或x＞2． 25．（7分）如图，海岛A四周20海里周围内为暗礁区，一艘货轮由东向西航行，在B处见岛A在北偏西60°，航行24海里到C，见岛A在北偏西30°，货轮继续向西航行，有无触礁的危险？请说明理由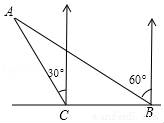．（  ） 【解答】解：如图，过点A作AD⊥BD于点D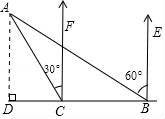，  ∵∠EBA=60°，∠FCA=30°， ∴∠ABC=∠BAC=30°． ∴AC=BC=24，∠DAC=30°． ∴AD=AC•cos30°=12  ≈20.78＞20．答：货轮继续向西航行，没有触礁危险． 26．（7分）阅读理解题：下面利用45°角的正切，求tan22.5°的值，方法如下： 解：构造Rt△ABC，其中∠C=90°，∠B=45°，如图． 延长CB到D，使BD=AB，连接AD，则∠D=  ∠ABC=22.5°．设AC=a，则BC=a，AB=BD=  a．又∵CD=BD+CB=（1+  ）atan22.5°=tan∠D= ﹣1请你仿照此法求tan15°的值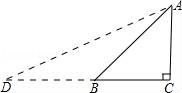．  【解答】解：构造Rt△ABC，其中∠C=90°，∠ABC=30°，[来源:Zxxk.Com] 延长CB到D，使BD=AB，连接AD， 则∠D= ∠ABC=15°，设AC=a，则由构 造的三角形得：AB=2a，BC= a，BD=2a，则CD=2a+ a=（2+）a，∴tan15°=tanC= 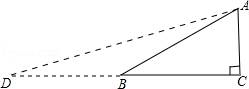 = =2﹣． 27．（8分）如图，抛物线y= x2+bx﹣2与x轴交于A，B两点，与y轴交于C点，且A（﹣1，0）．（1）求抛物线的解析式及顶点D的坐标； （2）判断△ABC的形状，证明你的结论； （3）点M（m，0）是x轴上的一个动点，当MC+MD的值最小时，求m的值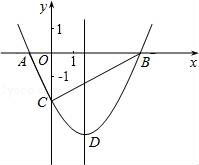．  【解答】解：（1）∵点A（﹣1，0）在抛物线y= x2+bx﹣2上，∴ ×（﹣1 ）2+b×（﹣1）﹣2=0，解得b= ∴抛物线的解析式为y= x2﹣ x﹣2．y=  x2﹣ x﹣2= （ x2﹣3x﹣4 ）= （x﹣）2﹣ ，∴顶点D的坐标为 （  ，﹣ ）．（2）当x=0时y=﹣2，∴C（0，﹣2），OC=2． 当y=0时， x2﹣x﹣2=0，∴x1=﹣1， x2=4，∴B （4，0）∴OA=1，OB=4，AB=5． ∵AB2=25，AC2=OA2+OC2=5，BC2=OC2+OB2=20， ∴AC2+BC2=AB2．∴△ABC是直角三角形． （3）作出点C关于x轴的对称点C′，则C′（0，2），OC′=2， 连接C′D交x轴于点M，根据轴对称性及两点之间线段最短可知，MC+MD的值最小． 解法一：设抛物线的对称轴交x轴于点E． ∵ED∥y轴，∴∠OC′M=∠EDM，∠C′OM=∠DEM ∴△C′OM∽△DEM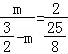． ∴  ∴  ，∴m=  ．解法二：设直线C′D的解析式为y=kx+n， 则 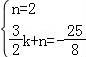 ，解得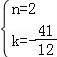：  ．∴  ．∴当y=0时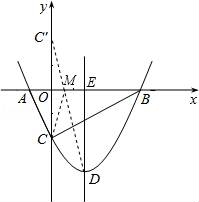，  ， ．∴  ． 28．（8分）如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根． （1）求C点坐标； （2）求直线MN的解析式； （3）在直线MN上存在点P，使以点P，B，C三点为顶点的三角形是等腰三角形，请直接写 出P点的坐标． 【解答】解：（1）解方程x2﹣14x+48=0得 x1=6，x2=8． ∵OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根， ∴OC=6，OA=8． ∴C（0，6）； （2）设直线MN的解析式是y=kx+b（k≠0）． 由（1）知，OA=8，则A（8，0）． ∵点A、C都在直线MN上， ∴  ，解得，  ，∴直线MN的解析式为y=﹣  x+6；（3）∵A（8，0），C（0，6）， ∴根据题意知B（8，6）． ∵点P在直线MNy=﹣ x+6上，∴设P（a，﹣ a+6）当以点P，B，C三点为顶点的三角形是等腰三角形时，需要分类讨论： ①当PC=PB时，点P是线段BC的中垂线与直线MN的交点，则P1（4，3）； ②当PC=BC时，a2+（﹣ a+6﹣6）2=64，解得，a=  ，则P2（﹣ ， ），P3（， ）；③当PB=BC时，（a﹣8）2+（ a﹣6+6）2=64，解得，a=  ，则﹣a+6=﹣ ，∴P4（，﹣ ）．综上所述，符合条件的点P有：P1（4，3），P2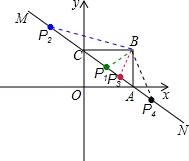（﹣  ， ）P3（， ），P4（ ，﹣）． (责任编辑：admin) |